高中数学 1.1.2《弧度制和弧度制与角度制的换算》教案1 新人教B版必修4VIP专享VIP免费

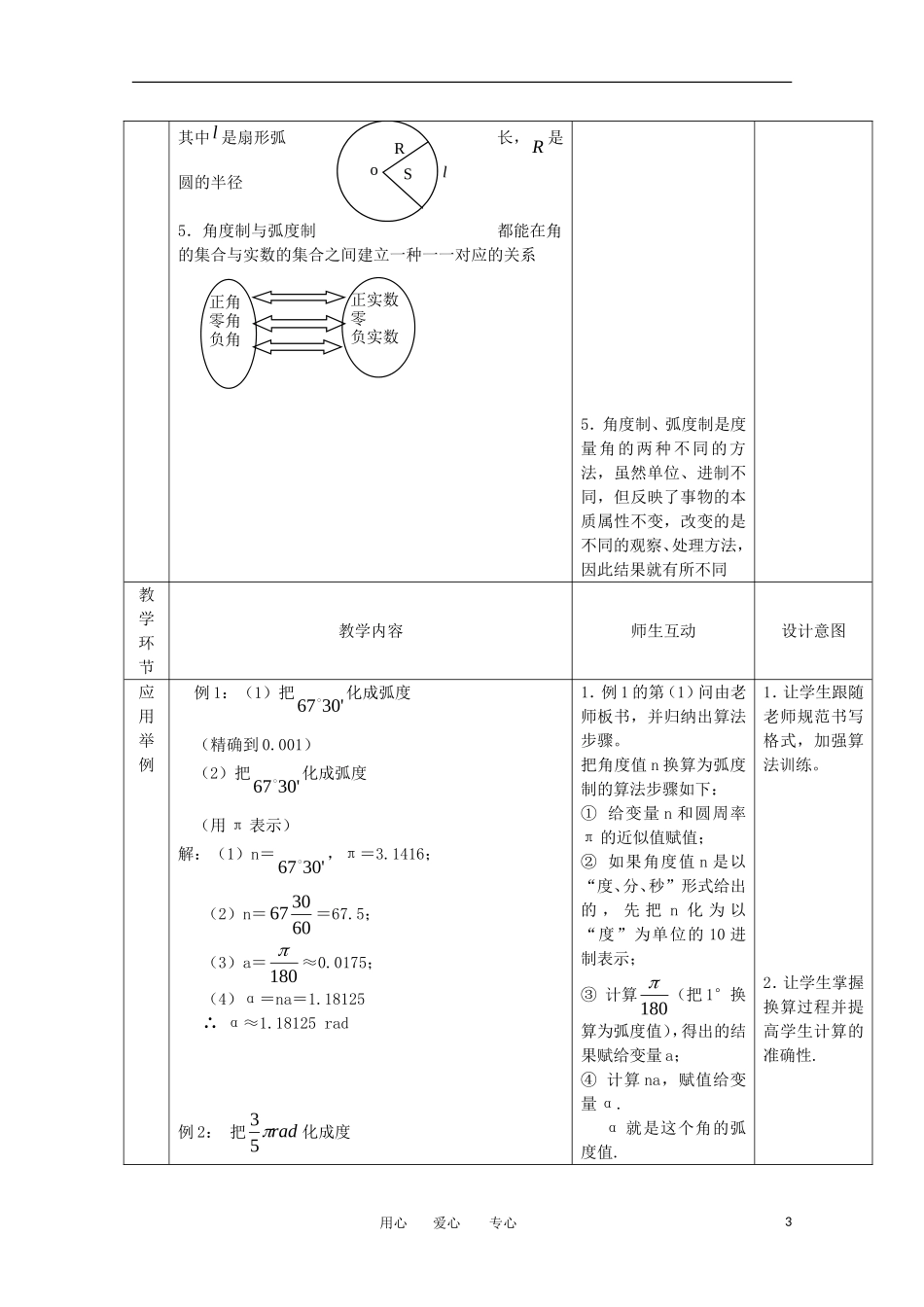
1.1.2弧度制和弧度制与角度制的换算一、教学目标1．知识目标：①了解弧度制，能进行弧度与角度的换算.②认识弧长公式，能进行简单应用.对弧长公式只要求了解，会进行简单应用，不必在应用方面加深.2.能力目标：①了解弧度制引入的必要性及弧度制与角度制的区别与联系.②了解角的集合与实数集建立了一一对应关系，培养学生学会用函数的观点分析、解决问题.③通过角度制与弧度制的换算，对学生进行算法训练，提高学生的计算能力.3．情感目标：使学生认识到角度制、弧度制都是角的度量制度，二者虽单位不同，但是二者相互联系、辩证统一.进一步加强学生对辩证统一思想的理解.二、教学重点、难点重点：了解弧度制，并能进行弧度与角度的换算.难点：弧度的概念及其与角度的关系.三、教学方法自学—讨论—讲授—练习先由学生自学，而后教师设置一些问题供学生思考，在此基础上，可以通过讲授再现概念，通过练习理解概念，完成教学.四、教学过程教学环节教学内容师生互动设计意图复习引入1、复习初中学习过的知识：角的度量、圆心角的度数与弧的度数及弧长的关系.2、复习角的概念推广：ABαO一条射线由原来的位置OA，绕着它的端点O按逆时针方向旋转到另一位置OB，就形成角α．旋转开始时的射线OA叫做角α的始边，旋转终止的射线OB叫做角α的终边，射线的端点O叫做角α的顶点．角分为正角、负角、零角。教师提出问题：①初中的角是如何度量的？度量单位是什么？学生回答：②1°的角是如何定义的？弧长公式是什么？学生回答：③角的范围是什么？如何分类的？温故而知新概念形1．初中学习中我们知道角的度量单位是度、分、秒，它们是60进制，角是否可以用其它单位度量，是否可以采用10进制？1．学生自学课本第7、8页.通过自学回答老师提出的以下问题：1．引导学生切身感受角的弧度制引入的必用心爱心专心1成2．通过自学，老师引导，总结1弧度角的定义、角的弧度与角的关系。①1弧度角的定义：长度等于半径长的弧所对的圆心角称为1弧度的角它的单位是rad①角的弧度制是如何引入的？②为什么要引入弧度制？好处是什么？③1弧度是如何定义的？④角度制与弧度制的区别与联要性.2．通过学生自学、老师引导加深学教学环节教学内容师生互动设计意图概念形成读作弧度，这种用“弧度”做单位来度量角的制度叫做弧度制．②平角、周角的弧度数：平角=rad、周角=2rad③正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是0④角的弧度数的绝对值rl（l为弧长，r为半径）3．角度制与弧度制的换算： 360=2rad∴180=rad∴1=radrad01745.0180'185730.571801rad4．用弧度制表示弧长及扇形面积公式：①弧长公式：rl由公式：rlrl比公式180rnl简单弧长等于弧所对的圆心角（的弧度数）的绝对值与半径的积②扇形面积公式lRS21系.2．学生动手画图来探究：①平角、周角的弧度数②角的弧度制与角的大小有关，与角所在圆的半径的大小是否有关？③角的弧度与角所在圆的半径、角所对的弧长有何关系？3．角度制与弧度制如何换算？4．初中学过用角度制计算弧长及扇形面积，现在用角的弧度制如何计算弧长及扇形面积呢？生对弧度制的理解。3．学生亲手作图，感受角的弧度制与角度制都是角的度量单位，都可以刻画角的大小，与角所在圆的半径无关。3．引导学生从弧度定义出发归纳出角度制与弧度制的换算公式。4．进一步巩固弧度定义，从不同角度加深学生对弧度制的理解。用心爱心专心2其中l是扇形弧长，R是圆的半径5．角度制与弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系5．角度制、弧度制是度量角的两种不同的方法，虽然单位、进制不同，但反映了事物的本质属性不变，改变的是不同的观察、处理方法，因此结果就有所不同教学环节教学内容师生互动设计意图应用举例例1：（1）把'3067化成弧度（精确到0.001）（2）把'3067化成弧度（用π表示）解：（1）n＝'3067，π＝3.1416；（2）n＝603067＝67.5；（3）a＝180≈0.0175；（4）α＝na＝1.18125∴α≈1.18125rad例2：把rad53化成度1．例1的第（1）问由老师板书，并归纳...