Matlab数据拟合实用教程VIP免费

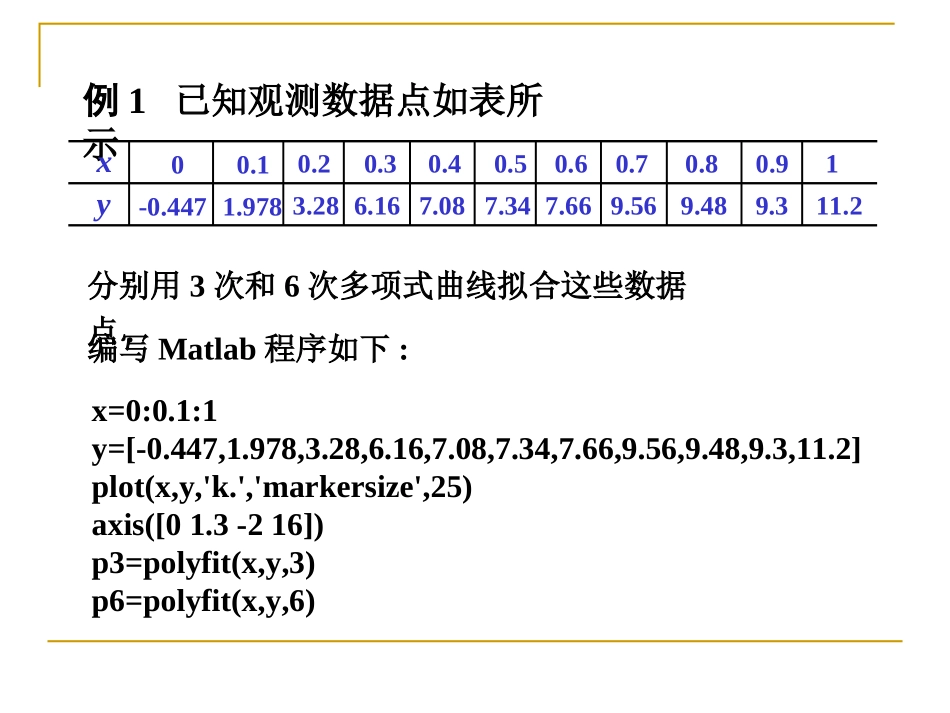
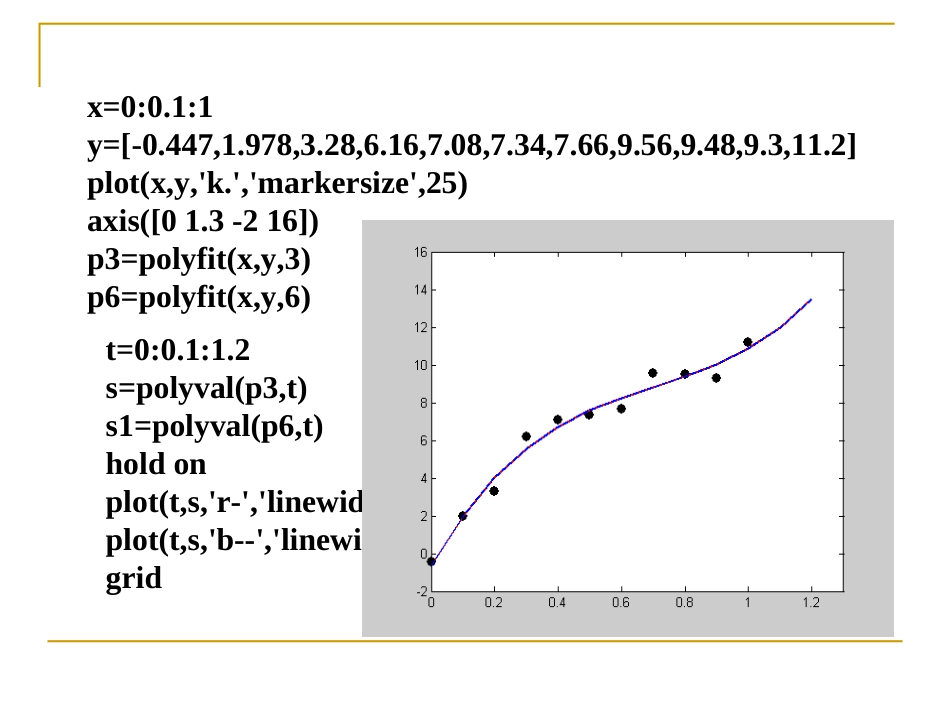
用Matlab进行数据拟合1.多项式曲线拟合:polyfit.y0=polyval(p,x0)p=polyfit(x,y,m)其中,x,y为已知数据点向量,分别表示横,纵坐标,m为拟合多项式的次数,结果返回m次拟合多项式系数,从高次到低次存放在向量p中.可求得多项式在x0处的值y0.例1已知观测数据点如表所示xy0-0.4470.11.9780.23.280.36.160.47.080.57.340.67.660.79.560.89.480.99.3111.2分别用3次和6次多项式曲线拟合这些数据点.x=0:0.1:1y=[-0.447,1.978,3.28,6.16,7.08,7.34,7.66,9.56,9.48,9.3,11.2]plot(x,y,'k.','markersize',25)axis([01.3-216])p3=polyfit(x,y,3)p6=polyfit(x,y,6)编写Matlab程序如下:t=0:0.1:1.2s=polyval(p3,t)s1=polyval(p6,t)holdonplot(t,s,'r-','linewidth',2)plot(t,s,'b--','linewidth',2)gridx=0:0.1:1y=[-0.447,1.978,3.28,6.16,7.08,7.34,7.66,9.56,9.48,9.3,11.2]plot(x,y,'k.','markersize',25)axis([01.3-216])p3=polyfit(x,y,3)p6=polyfit(x,y,6)例2用切削机床进行金属品加工时,为了适当地调整机床,需要测定刀具的磨损速度.在一定的时间测量刀具的厚度,得数据如表所示:切削时间t/h030.0129.1228.4328.1428.0527.7627.5727.2827.0刀具厚度y/cm切削时间t/h926.81026.51126.31226.11325.71425.31524.81624.0刀具厚度y/cm解:描出散点图,在命令窗口输入:t=[0:1:16]y=[30.029.128.428.128.027.727.527.227.026.826.526.326.125.725.324.824.0]plot(t,y,'*')解:描出散点图,在命令窗口输入:t=[0:1:16]y=[30.029.128.428.128.027.727.527.227.026.826.526.326.125.725.324.824.0]plot(t,y,'*')a=-0.301229.3804holdonplot(t,y1),holdoffa=polyfit(t,y,1)y1=-0.3012*t+29.3804例2用切削机床进行金属品加工时,为了适当地调整机床,需要测定刀具的磨损速度.在一定的时间测量刀具的厚度,得数据如表所示:切削时间t/h030.0129.1228.4328.1428.0527.7627.5727.2827.0刀具厚度y/cm切削时间t/h926.81026.51126.31226.11325.71425.31524.81624.0刀具厚度y/cm拟合曲线为:y=-0.3012t+29.3804例3一个15.4cm×30.48cm的混凝土柱在加压实验中的应力-应变关系测试点的数据如表所示1.552/N/m2//N/m65001033.103102.47610001032.465102.93615001031.953103.03620001031.51710已知应力-应变关系可以用一条指数曲线来描述,即假设21kke式中,表示应力,单位是N/m2;表示应变.2.89623751031.21910已知应力-应变关系可以用一条指数曲线来描述,即假设21kke式中,表示应力,单位是N/m2;表示应变.解选取指数函数作拟合时,在拟合前需作变量代换,化为k1,k2的线性函数.于是,12lnlnkk令0211ln,,lnzakak即01zaa在命令窗口输入:x=[500*1.0e-61000*1.0e-61500*1.0e-62000*1.0e-62375*1.0e-6]y=[3.103*1.0e+32.465*1.0e+31.953*1.0e+31.517*1.0e+31.219*1.0e+3]z=log(y)a=polyfit(x,z,1)k1=exp(8.3009)w=[1.552.472.933.032.89]plot(x,w,'*')y1=exp(8.3009)*x.*exp(-494.5209*x)plot(x,w,'*',x,y1,'r-')已知应力-应变关系可以用一条指数曲线来描述,即假设21kke式中,表示应力,单位是N/m2;表示应变.拟合曲线为:3-494.52094.027510e0211ln,,ln,zakak01zaa0211-494.5209,ln8.3009,akak3124.027510,494.5209kk令则求得于是在实际应用中常见的拟合曲线有:01yaxa直线101nnnyaxaxa多项式一般n=2,3,不宜过高.01ayax双曲线(一支)bxyae指数曲线2.非线性曲线拟合:lsqcurvefit.功能:x=lsqcurvefit(fun,x0,xdata,ydata)[x,resnorm]=lsqcurvefit(fun,x0,xdata,ydata)根据给定的数据xdata,ydata(对应点的横,纵坐标),按函数文件fun给定的函数,以x0为初值作最小二乘拟合,返回函数fun中的系数向量x和残差的平方和resnorm.例4已知观测数据点如表所示xy03.10.13.270.23.810.34.50.45.180.560.67.050.78.560.89.690.911.25113.17求三个参数a,b,c的值,使得曲线f(x)=aex+bx2+cx3与已知数据点在最小二乘意义上充分接近.首先编写存储拟合函数的函数文件.functionf=nihe...