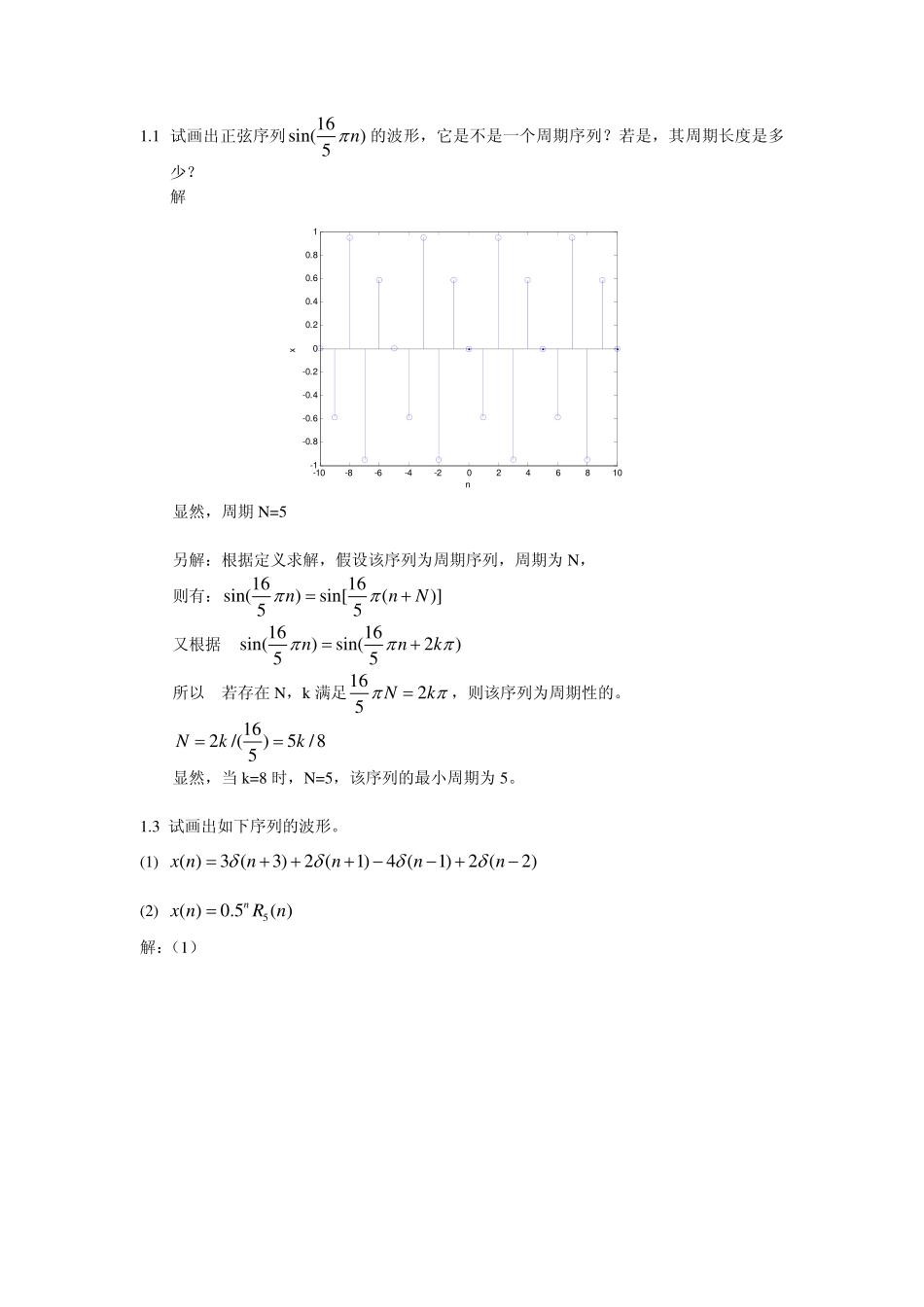
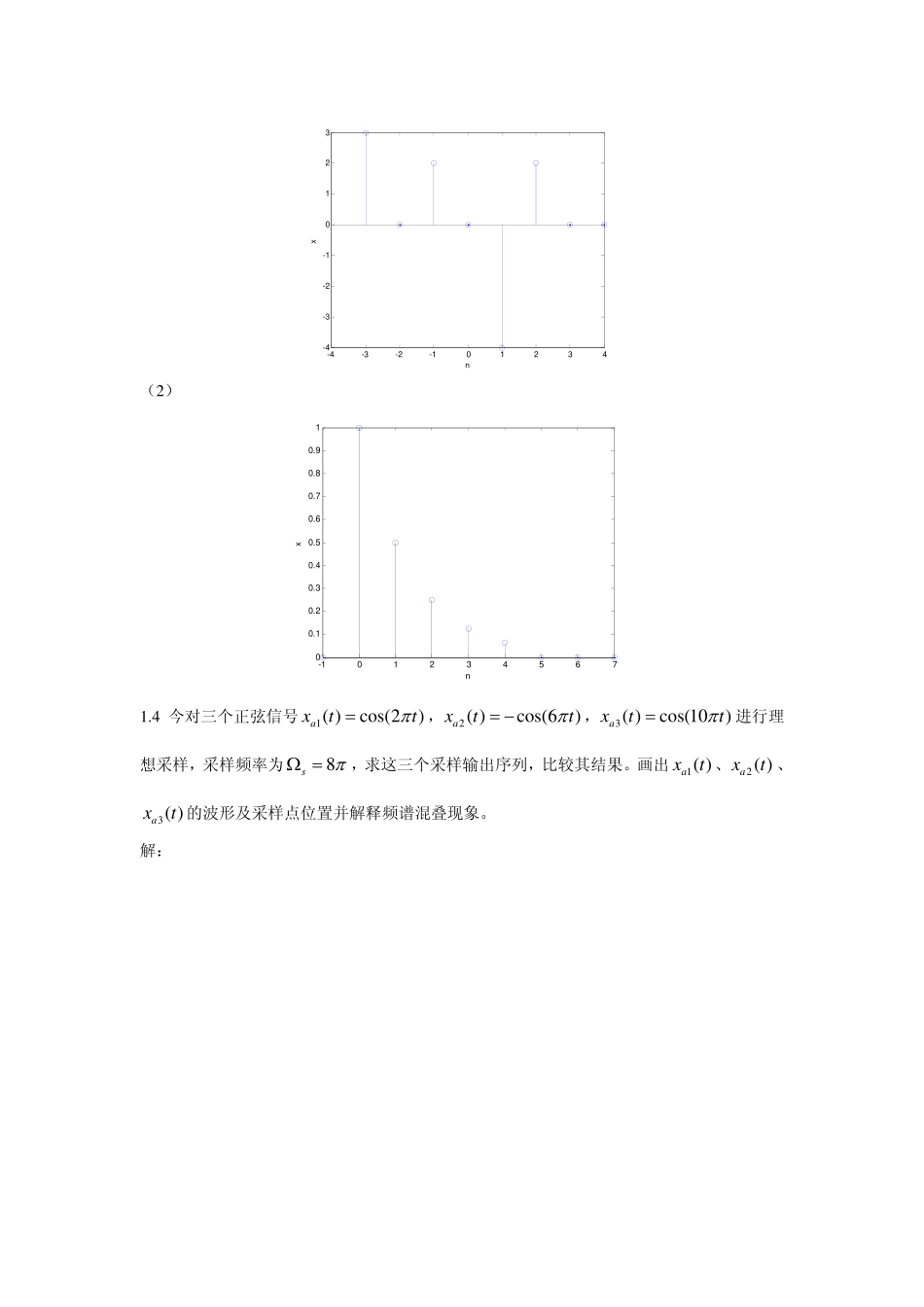
1.1试画出正弦序列16sin()5nπ的波形,它是不是一个周期序列?若是,其周期长度是多少?解-10-8-6-4-20246810-1-0.8-0.6-0.4-0.200.20.40.60.81nx显然,周期N=5另解:根据定义求解,假设该序列为周期序列,周期为N,则有:1616sin()sin[()]55nnNππ=+又根据1616sin()sin(2)55nnkπππ=+所以若存在N,k满足1625Nkππ=,则该序列为周期性的。162/()5/85Nkk==显然,当k=8时,N=5,该序列的最小周期为5。1.3试画出如下序列的波形。(1)()3(3)2(1)4(1)2(2)xnnnnnδδδδ=+++−−+−(2)5()0.5()nxnRn=解:(1)-4-3-2-101234-4-3-2-10123nx(2)-10123456700.10.20.30.40.50.60.70.80.91nx1.4今对三个正弦信号1()cos(2)axttπ=,2()cos(6)axttπ=−,3()cos(10)axttπ=进行理想采样,采样频率为8sπΩ=,求这三个采样输出序列,比较其结果。画出1()axt、2()axt、3()axt的波形及采样点位置并解释频谱混叠现象。解:-1-0.8-0.6-0.4-0.200.20.40.60.81-101txa1xa1(t)=cos(2*pi*t)-1-0.8-0.6-0.4-0.200.20.40.60.81-101txa2xa2(t)=-cos(6*pi*t)-1-0.8-0.6-0.4-0.200.20.40.60.81-101txa3xa3(t)=cos(10*pi*t)图1连续信号-1-0.8-0.6-0.4-0.200.20.40.60.81-101txa1xa1(t)=cos(2*pi*t)-1-0.8-0.6-0.4-0.200.20.40.60.81-101txa2xa2(t)=-cos(6*pi*t)-1-0.8-0.6-0.4-0.200.20.40.60.81-101txa3xa3(t)=cos(10*pi*t)图2对连续信号进行采样-4-3-2-101234-101nxa1xa1(t)=cos(2*pi*t)以角频率8pirad/s采样后的序列-4-3-2-101234-101nxa2xa2(t)=-cos(6*pi*t)以角频率8pirad/s采样后的序列-4-3-2-101234-101nxa3xa3(t)=cos(10*pi*t)以角频率8pirad/s采样后的序列图3采样后得到的序列-60-40-200204060-200204060omegaXa1(omega)xa1(t)=cos(2*pi*t)以8pirad/s采样后序列的幅频响应-60-40-2002040600204060omegaXa1(omega)xa1(t)=cos(2*pi*t)的幅频响应图4连续信号xa1(t)及采样后信号的幅频响应-40-30-20-100102030400510omegaXa3(omega)xa3(t)=cos(10*pi*t)的幅频响应-40-30-20-100102030400510omegaXa3(omega)xa3(t)=cos(10*pi*t)以8*pirad/s频率采样后序列的幅频响应图5连续信号xa3(t)及采样后信号的幅频响应对连续信号进行采样,设采样频率为sΩ,则采样后的信号对应的频谱会以sΩ为周期进行周期延拓,当原连续信号最高频率小于/2sΩ,则通过带宽为/2sΩ的理想低通滤波器就能把原信号恢复出来。如图4,原连续信号xa1(t)的角频率为2πrad/s,采样频率为8πrad/s=4*(2π),大于原连续信号频率的2倍,观察采样后的频谱可发现,通过带宽4πrad/s的低通滤波器就能恢复原信号。而当原信号最高频率大于/2sΩ时,在采样频率中,各调制频率会互相交叠起来,这就是频谱混叠现象。如图5,原连续信号xa1(t)的角频率为10πrad/s,采样频率为8πrad/s=4*(2π),为原连续信号频率的4/5,小于原信号最高频率的2倍,这时采样后的信号则发生了频谱的混叠现象。1.5一个采样周期为T的采样器,开关导通时间为τ,0Tτ<<,若采样器的输入信号为()axt,求采样器的输出信号�()()()paxtxtpt=的频谱结构。式中,1,0()(),()0,ntptrtnTrtτ∞=−∞≤≤⎧=−=⎨⎩∑其他解:这题为实际采样模型由于()pt为周期函数,故仍可展成傅里叶级数()sjmtmmptae∞Ω=−∞=∑其中:/2/20sin()112()2ssssTjmtjmtjmmTsmaptedtedtemTTTτττττ−Ω−Ω−Ω−Ω===Ω∫∫�/2/2()/2()()()sin()2()()2sin()2()()2sin()2()()2(()2sssssjtpasjmjmtjtasmsjmjmtasmsjmassmsXjxtptedtmxteeedtmTmextedtmTmeXjjmmTmSaTττττττττττττττ∞−Ω−∞∞∞−ΩΩ−Ω−∞=−∞∞∞−Ω−Ω−Ω−∞=−∞∞−Ω=−∞Ω=Ω=ΩΩ=ΩΩ=Ω−ΩΩΩ=∫∑∫∑∫∑/2)()sjmasmeXjjmτ∞−Ω=−∞Ω−Ω∑1.6令x(n)和()jXeω表示一个序列及其DTFT,并且x(n)为实因果序列,利用()jXeω求下面各序列的DTFT。(1)()kxn,k为任意常数解:n=-n=-DTFT[()]=()()()jnjnjkxnkxnekxnekXeωωω∞∞−−∞∞==∑∑(3)()(2)gnxn=解:()DTFT[g(n)]jGeω=n=-n=-=()(2)jnjngnexneωω∞∞−−∞∞=∑∑2mn=令/2/2/2m=-,m=-/2/2/2(/2)m=-m=-/2/21()()[()(1)()]211[()()...