双曲线的几何性质2VIP免费

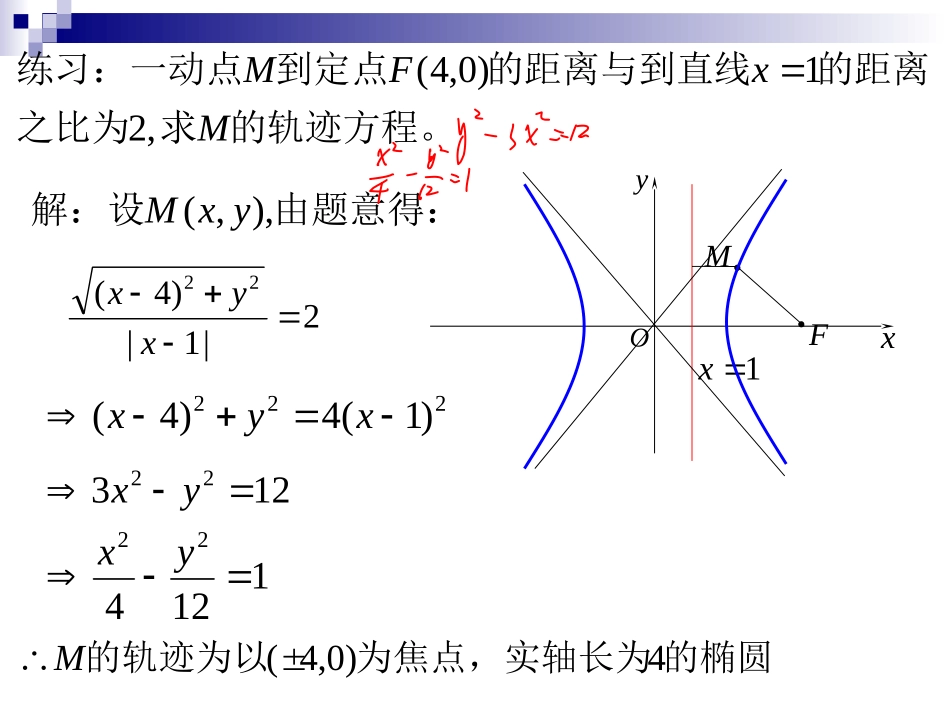
方程性质)0(12222babyax)0,0(12222babyax图形范围bybaxa,Ryaxax,或对称性轴及原点对称关于yx,轴及原点对称关于yx,顶点坐标),0(),,0()0,(),0,(2121bBbBaAaA)0,(),0,(21aAaA叫短轴叫长轴2121,BBAA叫虚轴叫实轴2121,BBAA离心率)10(,eace)1(,eace)0,0(,12222babyax双曲线叫做双曲线的渐进线直线xaby222222221byaxbyax的渐进线为双曲线等轴双曲线2exyOxabyxaby0的轨迹方程。求之比为的距离的距离与到直线到定点练习：一动点MxFM,21)0,4(MFOxy1x由题意得：解：设),,(yxM2|1|)4(22xyx222)1(4)4(xyx12322yx112422yx的椭圆为焦点，实轴长为的轨迹为以4)0,4(M双曲线的第二定义椭圆的第二定义：.)10(圆，则这个点的轨迹是椭是常数的距离的比线的距离和它到一条定直与一个定点动点eacelFM.是椭圆的离心率准线，常数直线叫做椭圆的定点是椭圆的焦点，定exyl'l..F2F1O.Md.)0(:)0()(2的轨迹，求点距离的比是常数的的距离和它到定直线，与定点，点MacaccaxlcFyxM解：xyl'l..FF’OM的距离，则到直线是点设lMd由题意知acdMF||d.||)(222accaxycx即化简.)()(22222222acayaxac，则设222bac12222byax方程化为)0,0(ba.22的双曲线、分别为的轨迹是实轴、虚轴长点baM.双曲线的第二定义：.)1(曲线，则这个点的轨迹是双是常数的距离的比线的距离和它到一条定直与一个定点动点eacelFM.是双曲线的离心率准线，常数定直线叫做双曲线的定点是双曲线的焦点，e.)0(1222222caxcFbyax，对应的右准线方程是，右焦点，对于双曲线.)0(21caxcF对应的左准线方程是，左焦点cayy2程是：轴上的双曲线的准线方焦点在yl'l..FF’OMd.x，求证：是双曲线右支上任意点）（的焦点－已知双曲线),(),0,(0,)0,0(100212222yxPcFcFbabyax例1证明：，01||exaPFP说明：|PF1|,|PF2|称为椭圆的焦半径，此公式称为焦半径公式cax2双曲线的左准线为：由双曲线的第二定义得accaxPF201||01|:|exaPF整理得：由双曲线的第一定义得0122||||exaaPFPFmin1||PFac为双曲线的离心率。其中eyl'l..F2F1O.02||exaPFxacmin2||PF|||,|),(),0,(0,)0,0(12100212222PFPFyxPcFcFbabyax，求是双曲线左支上任意点）（的焦点－已知双曲线练习证明：Pcax2双曲线的左准线为：由双曲线的第二定义得acxcaPF021||01|:|exaPF整理得：由双曲线的第一定义得0122||||exaaPFPFyl'l..F2F1O.x。到双曲线左准线的距离求点，到右焦点的距离等于右支上一点：已知双曲线例PPyx813664222解：，、为到左、右准线距离分别设ddP'edPF||2则ePFd||2两准线间的距离：由双曲线的第二定义得Pyl'l..F2F1O.6822＋bacba，，105324585642)(222cacaca596532564/dx解2：451edPF：由双曲线的第一定义得24||2||21PFaPF＋：由双曲线的第二定义得。到双曲线左准线的距离求点，到右焦点的距离等于右支上一点：已知双曲线例PPyx813664222Pyl'l..F2F1O.6822＋bacba，，10596||1ePFd。到双曲线左准线的距离求点，到右焦点的距离等于上一点思考：已知双曲线PPyx81366422的最小值求右支上一点，定点是双曲线的右焦点为：已知双曲线方程为例||53||),2,9(,116932222MFMAAMFyxMy..F2F1O.xA得：解：由双曲线第二定义)(,||2到右准线的距离为MdedMFdMF35||2即dMAMFMA||||53||2536599)|(|2mincaxdMAA的最小值。求曲线右支上一点，定点是双的右焦点为为练习：已知双曲线方程||||),2,9(,11692222MFMAAMFyxMy..F2F1O.xA得：解：由双曲线第一定义62||||21aMFMF6||||12MFMF即6||||||||12MFMAMFMA621062146||)6||(|221min1AFMFMA作业：何性质二《创新设计》双曲线几题、习题87:4.8