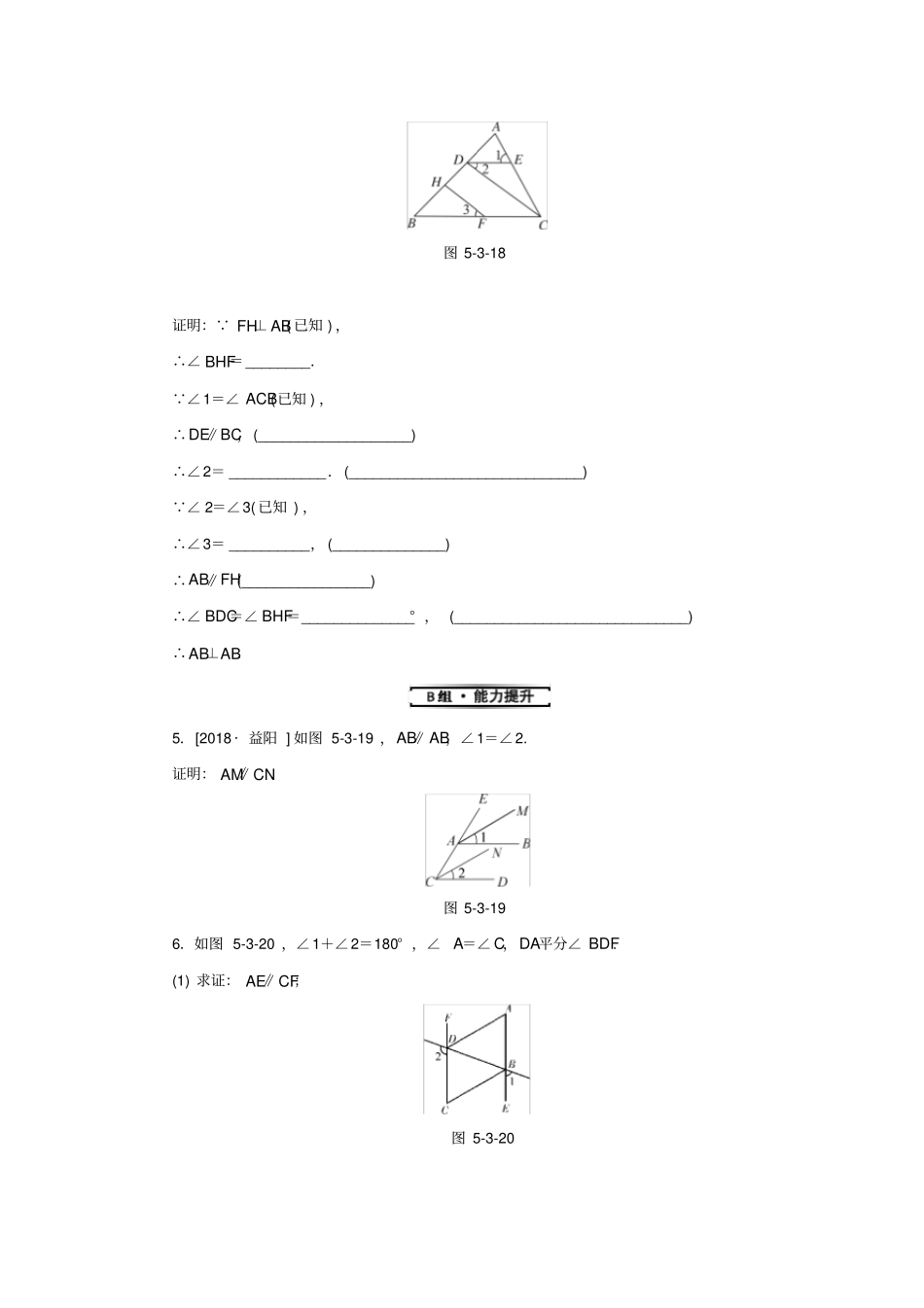
第五章相交线与平行线5.3.2命题、定理、证明1.下列命题是真命题的是()A.过直线外一点可以画无数条直线与已知直线平行B.如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°C.3条直线交于一点,对顶角最多有6对D.与同一条直线相交的两条直线相交2.如图5-3-17,直线a,b被直线c所截,下列说法正确的是()图5-3-17A.当∠1=∠2时,一定有a∥bB.当a∥b时,一定有∠1=∠2C.当a∥b时,一定有∠1+∠2=90°D.当∠1+∠2=180°时,一定有a∥b3.判断下列语句是不是命题,如果是命题,将其改写成“如果⋯⋯那么⋯⋯”的形式.(1)连接AB;(2)过直线外一点作已知直线的垂线;(3)对顶角相等;(4)等量可以代换;(5)圆的周长是2πr.4.[2018·徐州期末]填空并完成以下证明:如图5-3-18,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:AB⊥AB.图5-3-18证明:∵FH⊥AB(已知),∴∠BHF=________.∵∠1=∠ACB(已知),∴DE∥BC,(___________________)∴∠2=____________.(_____________________________)∵∠2=∠3(已知),∴∠3=__________,(______________)∴AB∥FH(________________)∴∠BDC=∠BHF=______________°,(_____________________________)∴AB⊥AB.5.[2018·益阳]如图5-3-19,AB∥AB,∠1=∠2.证明:AM∥CN.图5-3-196.如图5-3-20,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)求证:AE∥CF;图5-3-207.[2017春·宁城期末]有一天李明同学用“几何画板”画图,他先画了两条平行线AB,AB,然后在平行线间画了一点E,连接BE,DE后(如图5321①),他用鼠标左键点住点E,拖动后,分别得到如图5321②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?(2)请从所得的四个关系中,选一个说明它成立的理由.,①②③④图5-3-21参考答案【分层作业】1.C2.D3.解:(1)(2)不是命题.(3)是命题;如果两个角是对顶角,那么它们的大小相等.(4)是命题;如果两个量相等,那么这两个量可以互相代换.(5)是命题;如果一个图形是以r为半径的圆,那么它的周长是2πr.4.90°同位角相等,两直线平行∠BAB两直线平行,内错角相等∠BAB等量代换同位角相等,两直线平行90两直线平行,同位角相等5.证明:∵AB∥AB,∴∠EAB=∠AAB.∵∠1=∠2,∴∠EAB-∠1=∠AAB-∠2,即∠EAM=∠ACN,∴AM∥CN.6.(1)证明:∵∠1+∠2=180°,∠2+∠ABB=180°,∴∠ABB=∠1,∴AE∥CF.(2)解:BC平分∠DBE.理由:∵DA平分∠BDF,∴∠FDA=∠ADB.∵AE∥CF,∴∠A=∠FDA,∠FDB=∠EBD.∵∠A=∠C,∴∠FDA=∠C,∴AD∥CB,∴∠ADB=∠CBD,∴∠CBE=∠EBD-∠CBD=∠FDB-∠ADB=∠FDA=∠ADB=∠CBD,即BC平分∠DBE.7.解:(1)①∠B+∠D=∠BED;②∠B+∠D+∠BED=360°;③∠B=∠BED+∠D;④∠B=∠D+∠BED.(2)选择①.理由:如答图1,过E作AB∥AB.∵AB∥AB,∴AB∥AB,∴∠B=∠BAB,∠D=∠DAB,∴∠BED=∠BAB+∠DAB=∠B+∠D.选择②.理由:如答图2,过E作AB∥AB.∵AB∥AB,∴AB∥AB,∴∠B+∠BAB=180°,∠D+∠DAB=180°,∴∠B+∠BED+∠D=180°+180°=360°.选择③.理由:如答图3,延长AB交DE于点F.∵AB∥AB,∴∠D=∠BFE.∵∠ABE是△BAB的外角,∴∠ABE=∠BAB+∠BFE=∠BED+∠D.选择④.理由:如答图4,设AB与BE交于点F.∵AB∥AB,∴∠B=∠CFE,∵∠CFE是△DAB的外角,∴∠CFE=∠D+∠E,即∠B=∠D+∠BED.答图1答图2答图3答图4