相似三角形的判定(3)VIP免费

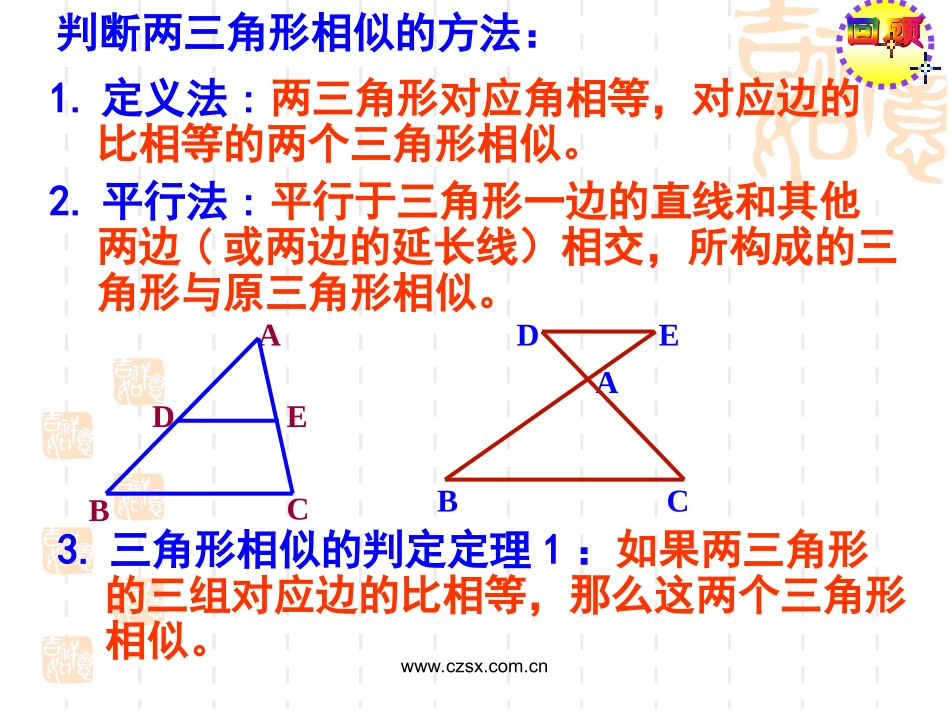
www.czsx.com.cn保康县熊绎中学九年级数学备课组www.czsx.com.cn1.定义法:两三角形对应角相等，对应边的比相等的两个三角形相似。判断两三角形相似的方法：DEABCABCDE2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线）相交，所构成的三角形与原三角形相似。3.三角形相似的判定定理1：如果两三角形的三组对应边的比相等，那么这两个三角形相似。如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。猜想？类似于判定三角形全等的SAS方法，我们能不能通过两边及其夹角来判定两个三角形相似呢？和利用刻度尺和量角器画ABC探究3相等呢？吗？另外两组角是否会于的长，它们的比值等和应边值，量出它们第三组对等于给定的都和使k'C'BBCk'C'AAC'B'AAB,'AA,'C'B'A改变k和∠A的值的大小,是否有同样的结论？中，和已知：在'C'B'AABC'AA,'C'AAC'B'AABABC'''CBA求证:△∽△ABC'A'B'CDE''''''CAEABADACBA∽DEΔA'，可得E交于点C'A'交CB∥DE再做D过点，ABDA'上截取B'A'证明：在线段'''''CAACCAEAABDACAACBAAB',''''又ABCDEA'ACEA''.AA又'''CBAABC∽如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。三角形相似的判定定理2：ABC中，和在'C'B'AABC'AA,'C'AAC'B'AAB∵'''CBAABC∽'A'B'Cwww.czsx.com.cn解:∵AB/A′B′=7/3AC/A′C′=14/6=7/3∴AB/A′B′=AC/A′C′又∠A＝∠A′＝60°∴△ABC∽△A′B′C′AB=7，AC=14，∠A＝60°A′B′＝3，A′C′＝6，∠A′＝60°AB=7，AC=14，∠A＝60°A’B’＝6，A’C’＝3，∠A’＝60°例1：根据下列条件，判断△ABC和△A’B’C’是否相似，并说明理由。变式变式练习：.5'C'A,4'C'B,3'B'A,10AC,8BC,6AB)1('C'B'AABC.1否相似，并说明理由。是和根据下列条件，判断oo40'A.6'C'A,4'B'A40A,10AC,20AB)2(2.图中两个三角形是否相似？63105CABDE2693414相似不相似相似不相似例2、如图，在△ABC中，P为AB上的一点，且AC2＝AP•AB，（1）判断△APC与△ACB的关系，并说明理由；（2）若AB=6,AC=3,BC=5,求PC的长。BCPA,23ECAEBDADBCDEADECB1、如图，已知试求的值；DAMBNC2、如图，在正方形ABCD中，点M、N分别在AB、BC上，AB＝4，AM＝1，BN＝0.75，（1）△ADM与△BMN相似吗？为什么？（2）求∠DMN的度数；3.如图，△ABC中，AB＝12，BC＝18，AC＝15，D为AC上一点，CD＝AC，在AB上找一点E，得到△ADE，若图中两个三角形相似，求AE的长；32ABCD相似三角形的判定方法：小结：1、定义判定法2、平行判定法比较复杂，烦琐只能在特定的图形里面使用3、三角形相似的判定定理1。4、三角形相似的判定定理2。