抛物线的几何性质VIP免费

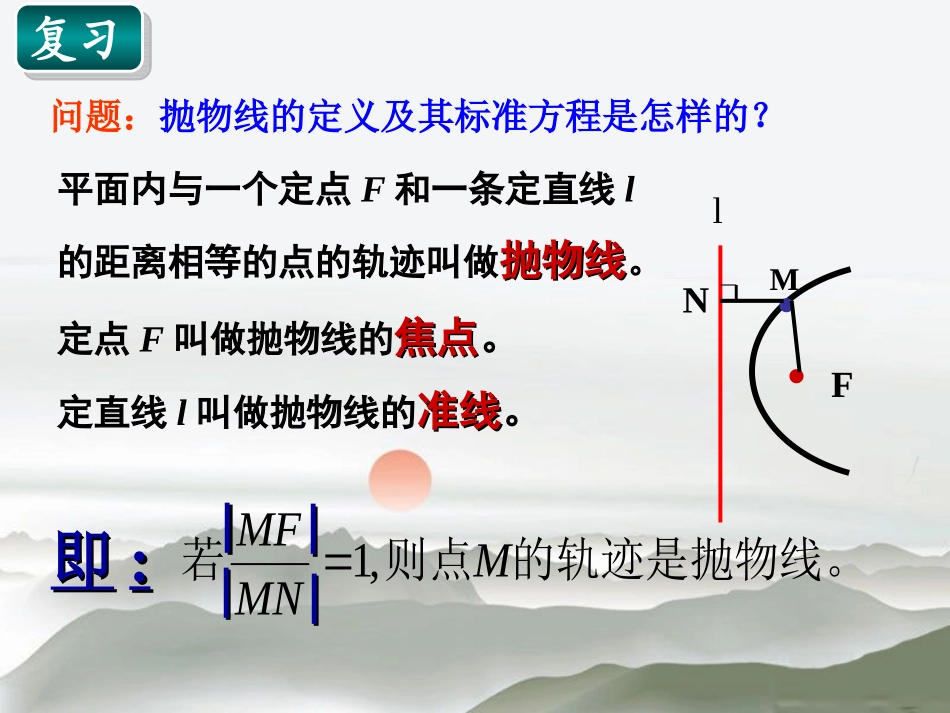
平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线抛物线。定点F叫做抛物线的焦点焦点。定直线l叫做抛物线的准线准线。的轨迹是抛物线。则点若MMNMF,1即即::︳︳︳︳︳︳︳︳··FMlN问题：抛物线的定义及其标准方程是怎样的？复习复习图形焦点准线标准方程yxo﹒﹒yxoyxo﹒yxo﹒练习：填空（顶点在原点，焦点在坐标轴上）方程焦点准线开口方向xy62yx420722yx)0,(23F)0,1(F)1,0(F),0(87F23x1x1y87yxy42开口向右开口向左开口向上开口向下以抛物线的标准方程：来研究它的几何性质．022ppxy（图形对称轴顶点离心率准线焦点）抛物线的几何性质抛物线的几何性质y2=2px•yy取全体实数取全体实数XY•XX00范围范围对称性对称性关于关于XX轴对称轴对称顶点顶点定义：抛物线定义：抛物线与对称轴的交点，与对称轴的交点，叫做抛物线的叫做抛物线的顶顶点点离心率离心率离心率离心率e=1e=1抛物线的几何性质抛物线的几何性质图形标准方程焦点坐标准线方程范围对称轴顶点离心率y2=2pxy2=-2pxx2=2pyx2=-2py)0,2(pF)0,2pF(-)2,0(pF)2,0(pF-2=px-2=px2=py2=py-x0，yRx0，yRy0，xRy0，xR原点即(0，0)e=1x轴y轴问题：与椭圆、双曲线的几何性质比较，抛物线的几何性质有什么特点？（1）抛物线只位于半个坐标平面内，虽然它也可以无限延伸，但没有渐近线；2）抛物线只有一条对称轴，没有对称中心；3）抛物线只有一个顶点、一个焦点、一条准线；4）抛物线只有一个顶点、一个焦点、一条准线；抛物线由P决定开口大小，P越大开口越大而椭圆、双曲线由e决定抛物线的顶点在原点，对称轴重合于椭圆短轴所在的直线，抛物线焦点到顶点的距离为3，求抛物线的方程及抛物线的准线方程。例1：求抛物线的标准方程及几何性质例1：求抛物线的标准方程及几何性质229436xy练习练习求符合下列条件的抛物线的标准方程（1）顶点在原点，关于x轴对称，并且经过点M（5，－4）；（2）顶点在原点，焦点是F（0，5）；（3）顶点在原点，准线是x=4；（4）焦点是F（0，－8），准线是y=8。22(0)(),_____,2ypxppaa1抛物线上一点M到焦点距离则点M到准线的距离是点M的横坐标是______.、是2.一条隧道的顶部是抛物拱形，拱高是1.1m，跨度是2.2m。求拱形的抛物线方程。练习练习例2斜率为1的直线Ｌ经过抛物线y2=4x的焦点,且与抛物线相交于A、B两点,求线段AB的长.xyoF(１,0)Ａx+１=0ＢＡ‘Ｂ‘法法3|3|ABAB|=|=xx11++xx22++PP法1利用两点间距离公式221212()()AByyxx法2212221211412()ABkxxkxxxx212(0)8ypxp经过焦点且斜率为的直线被抛物线所截得的弦长为，求抛物线方程。xyoFＡＢＡ‘Ｂ‘练习练习1.AB是抛物线x=y2的一条焦点弦，且｜AB｜=4，则AB的中点到直线x+1=0的距离为()(A)25(B)2(C)3(D)4112.点A的坐标为(3，1)，若P是抛物线24yx上的一动点，F是抛物线的焦点，则|PA|+|PF|的最小值为()(A)3(B)4(C)5(D)6DB练习练习例3:探照灯反射镜的轴截面是抛物线的一部分，光源位于抛物线的焦点处，已知灯口圆的直径为60cm,灯深40cm，求抛物线的标准方程及焦点的位置。FyxO解：如图所示，在探照灯的轴截面所在平面建立直角坐标系，使反光镜的顶点与原点重合，x轴垂直于灯口直径。AB设抛物线的标准方程是：由已知条件可得点A的坐标是（40，30），代入方程可得230240p22(0)ypxp454p所求的标准方程为焦点坐标为2252yx45(,0)8.022正三角形的边长）上，求这个（两个顶点在抛物线外顶点位于坐标原点，另探究：正三角形的一个ppxyyOxBA分析:观察图,正三角形及抛物线都是轴对称图形,如果能证明x轴是它们的公共的对称轴,则容易求出三角形的边长.线上，在抛物、的顶点解：如图，设正三角形BAOAByOxBA），则，）、（，且坐标分别为（2211yxyx.22222121pxypxy，，，所以：又22222121||||yxyxOBOA，即：022212221pxpxxx.022121））（（pxxxx，，，020021pxx.21xx.||||21轴对称关于，即线段由此可得xAByy，，且轴垂直于因为设oAOxABxyxA30),(11yOxBA.3330tan11oxy，pyx2211...