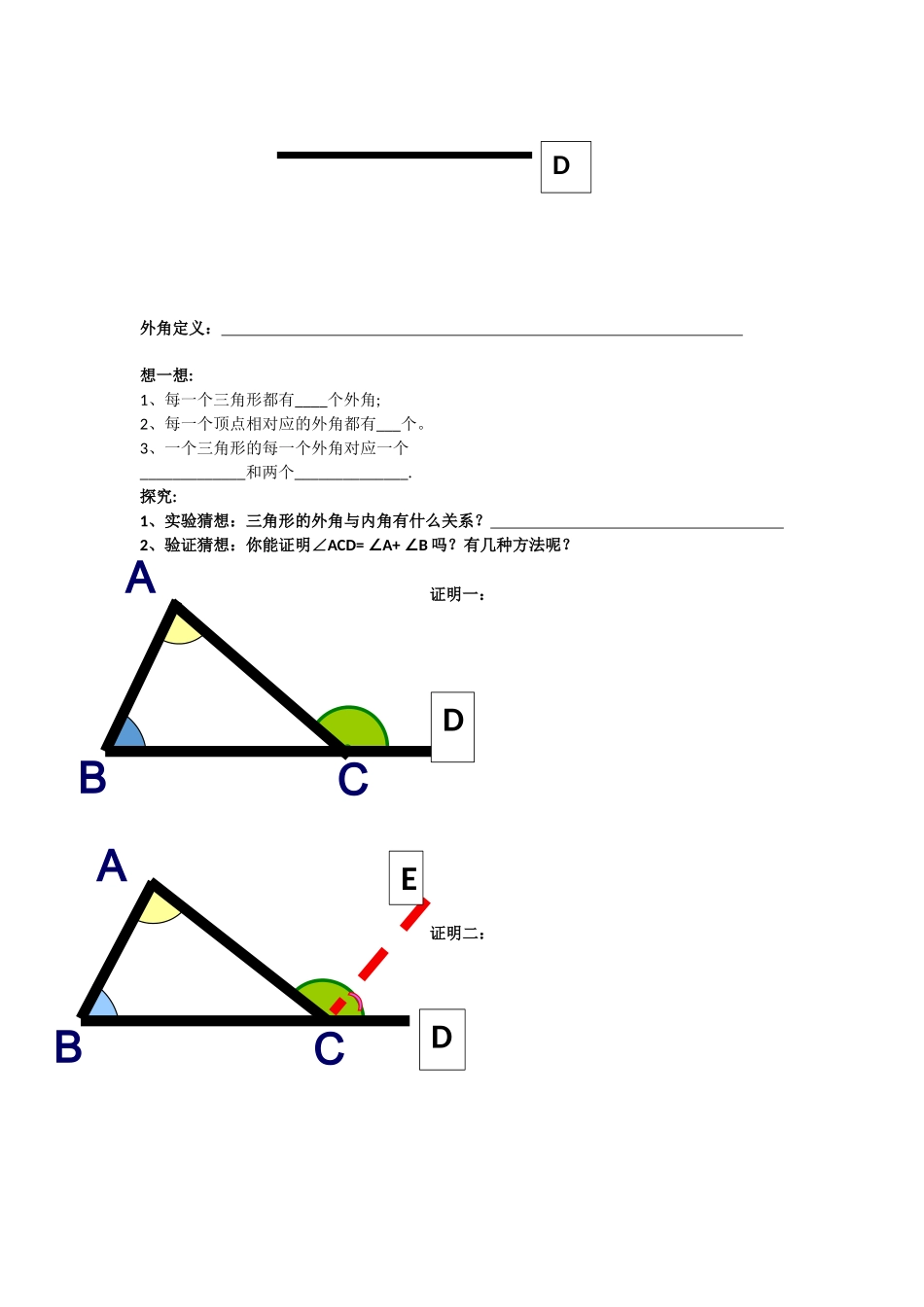
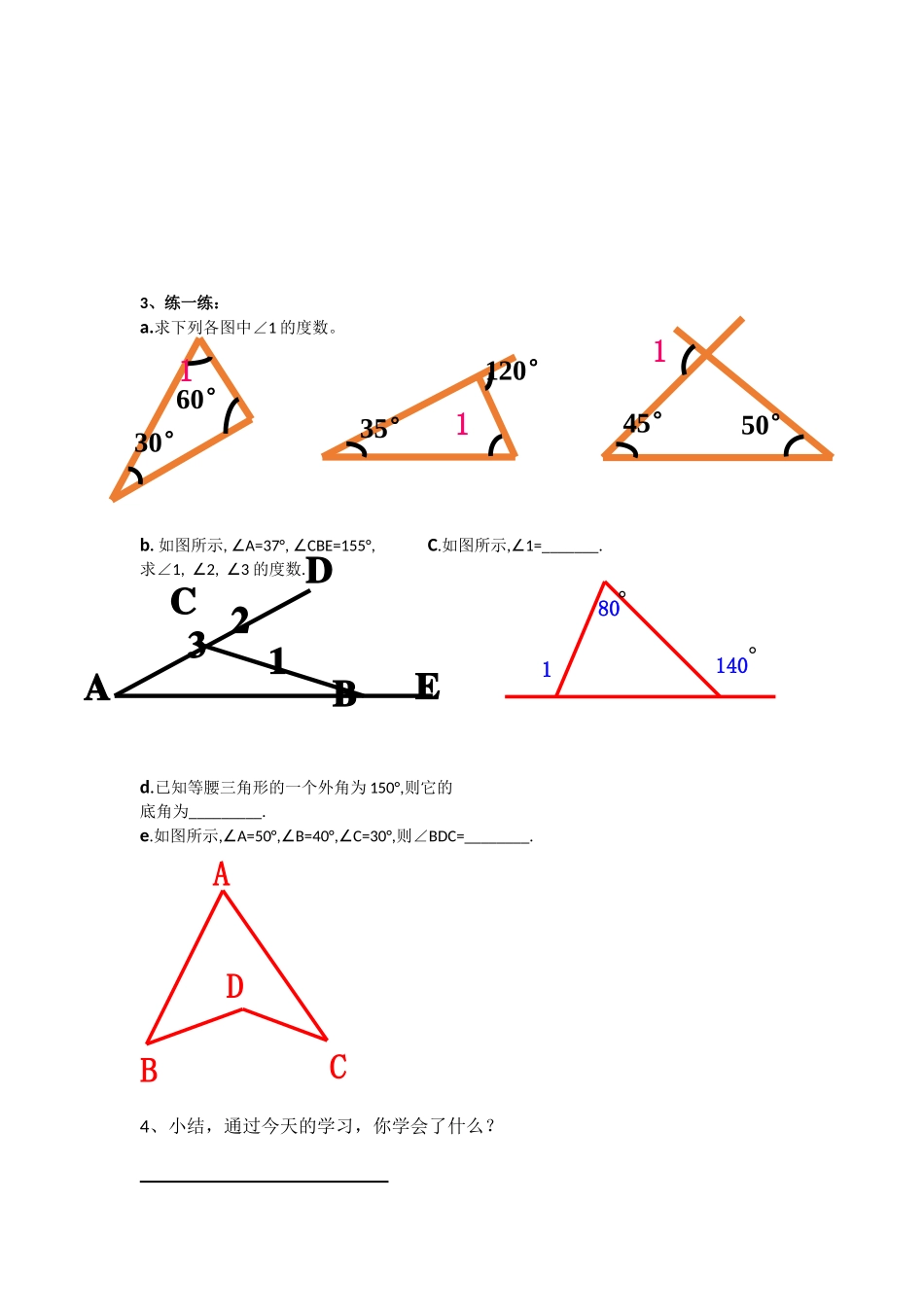
三角形的外角导学案一、学习目标:1、了解三角形的外角的定义;2、掌握三角形的外角与内角(相邻的内角和不相邻的内角)的关系;3、会运用与三角形有关的角解决问题。二、重点、难点:1、重点:三角形的外角的性质。2、难点:外角的定义及外角性质的论证过程。三、学习过程:1、复习旧知(1、)什么是三角形内角和定理?(2、)在ABC中,(1)∠C=90°,∠A=30°,则∠B=;(2)∠A=50°,∠B=C∠,则∠B=.2、探究新知CBA外角定义:想一想:1、每一个三角形都有____个外角;2、每一个顶点相对应的外角都有___个。3、一个三角形的每一个外角对应一个_____________和两个______________.探究:1、实验猜想:三角形的外角与内角有什么关系?2、验证猜想:你能证明∠ACD=A+B∠∠吗?有几种方法呢?证明一:证明二:DCBACBADDE3、练一练:a.求下列各图中∠1的度数。b.如图所示,A=37°,CBE=155°,∠∠C.如图所示,1=_______.∠求∠1,2,3∠∠的度数.d.已知等腰三角形的一个外角为150°,则它的底角为_________.e.如图所示,A=50°,B=40°,C=30°,∠∠∠则∠BDC=________.4、小结,通过今天的学习,你学会了什么?132EDCBA1°80°140ABCD160°30°1120°35°150°45°