1.2.4诱导公式VIP免费

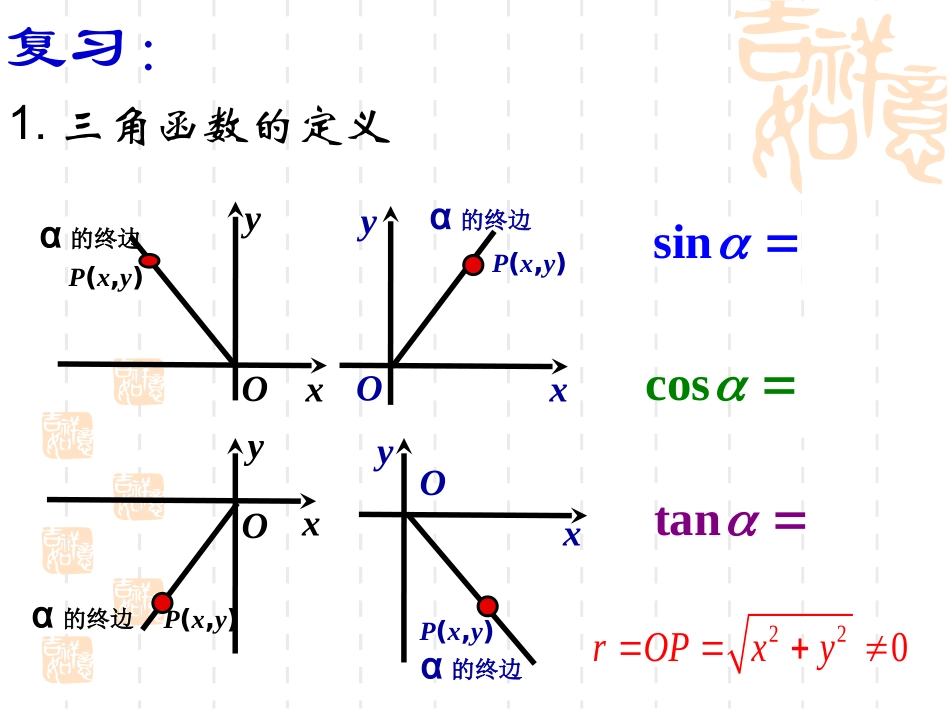
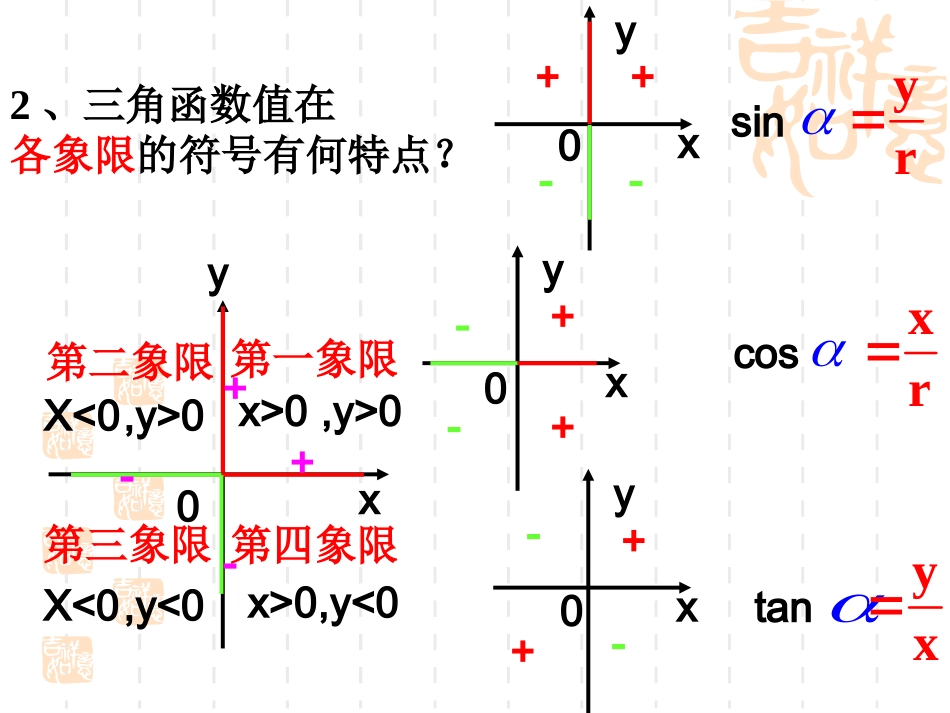
诱导公式（第1课时）yOxP(x,y)α的终边P(x,y)α的终边yOx1.三角函数的定义yOxP(x,y)α的终边P(x,y)α的终边yOxsinyrcosxrtanyx复习：220rOPxy2、三角函数值在各象限的符号有何特点？第三象限第一象限第四象限第二象限xy0++--x>0X<0X<0x>0,y>0,y>0,y<0,y<0++--xy0++--xy0++--xy0sinyrcosxrtanyx3公式（一）sin(360)sincos(360)costan(360)tankkkkZ其中sin(2)sincos(2)costan(2)tankkkkZ其中实质：终边相同，三角函数值相等用途：“大”角化“小”角新课讲解：思考1:π＋α（k∈Z）与α的终边关系是什么？xrα终边Л+α终边关于原点对称用定义计算yrxryxsin()cos()tan()sin()sincos()costan()tanα终边Л+α终边yryxsincostanxrxr公式二sin()3sin332cos(30180)cos3032tan()4tan41记忆方法：利用图形sin()sincos()costan()tan用途：“大”角化“小”角α终边Л+α终边思考2：α与-α的终边位置关系如何？α终边-α终边α与-α的终边关于x轴对称用定义计算yrxryxsincostansin()cos()tan()sin()sincos()costan()tanα终边-α终边xryryyxx公式三sin7505cos4sin()sincos()costan()tansin(750)29cos()419tan()3用途：负角化为正角记忆方法：利用图形19tan3思考3：和它们的终边关系是什么？α终边Л+α终边思考4：它们的终边关系是什么？和关于y轴对称用定义计算yrxryxsincostansin()cos()tan()sin()sincos()costan()tanα终边Л+α终边yrxryyxx公式四sin150sin()sincos()costan()tan公式四sin(18030)1cos120cos(18060)cos6023tantan()tan1444作用：钝角化为锐角记忆方法：利用图形1sin302sin()sincos()costan()tan公式四：sin()sincos()costan()tan公式二：sin()sincos()costan()tan公式三：公式一：sin(2)sincos(2)cos)tan(2)tan(kkkZk~2(),,kkZ公式一四可用下面的话来概括：的三角函数值，等于角的同名函数值，前面加上一个把看成锐角时原函数值的符号。sin()sincos()costan()tan公式二：sin()sincos()costan()tan公式三：sin()sincos()costan()tan公式四：公式一：sin(2)sincos(2)cos)tan(2)tan(kkkZk同名函数符号看象限利用诱导公式一～四，可以求任意角的三角函数，其基本思路是：化归与转化的数学思想.任意负角的三角函数任意正角的三角函数0～2π的角的三角函数锐角的三角函数化简口诀：负化正，正化小，化到锐角就行了.例2、将下列各三角函数化成锐角三角函数(1)sin(-699º)(2)cos(-1525º)(3)tan(-872º)(4)cos(92º)答案：(1)–sin21º(2)cos85º(3)tan28º(4)-sin2º例题225sin（1）；（2）；例3求下列三角函数值：1290cos(1)sin225解：sin(18045)sin4522(2)cos(1290)cos1290cos(2103360)cos210cos(18030)cos3032练习（1）；（2）．413sin1665cos求下列各三角函数：16sin(-)3;o（3）（4）cos-204043tan5611sin616sin(-)3;o（3）（4）cos-2040例题例3化简：．...