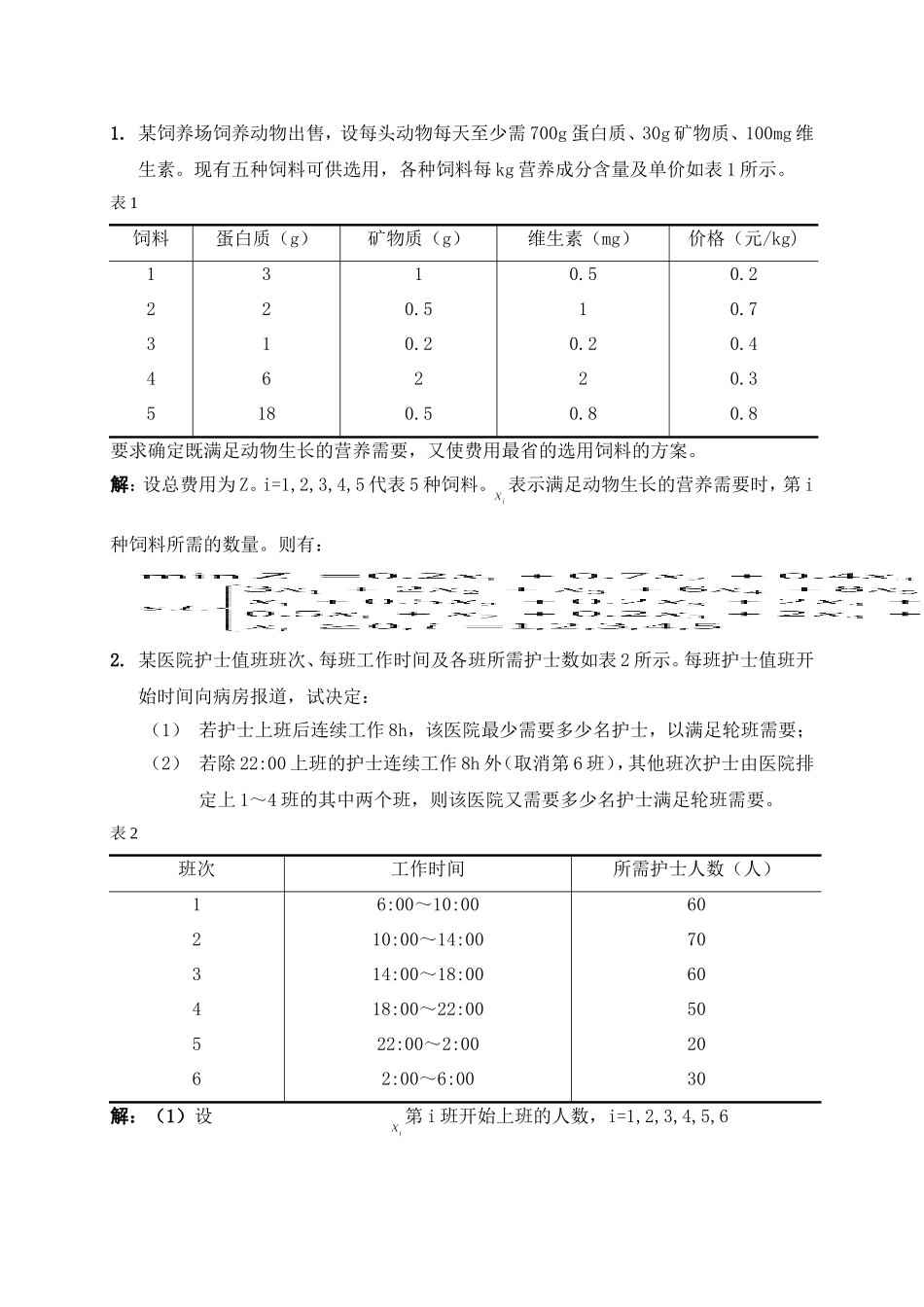
1.某饲养场饲养动物出售,设每头动物每天至少需700g蛋白质、30g矿物质、100mg维生素。现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如表1所示。表1饲料蛋白质(g)矿物质(g)维生素(mg)价格(元/kg)1310.50.2220.510.7310.20.20.446220.35180.50.80.8要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。解:设总费用为Z。i=1,2,3,4,5代表5种饲料。表示满足动物生长的营养需要时,第i种饲料所需的数量。则有:2.某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。每班护士值班开始时间向病房报道,试决定:(1)若护士上班后连续工作8h,该医院最少需要多少名护士,以满足轮班需要;(2)若除22:00上班的护士连续工作8h外(取消第6班),其他班次护士由医院排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要。表2班次工作时间所需护士人数(人)16:00~10:0060210:00~14:0070314:00~18:0060418:00~22:0050522:00~2:002062:00~6:0030解:(1)设第i班开始上班的人数,i=1,2,3,4,5,6解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。则设设第i班开始上班的人数,i=1,2,3,4。3.要在长度为l的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n种,分别为(j=1,2,…n)。问每种毛坯应当截取多少根,才能使圆钢残料最少,试建立本问题的数学模型。解:设表示各种毛坯的数量,i=1,2,…n。4.一艘货轮分前、中、后三个舱位,它们的与最大允许载重量如表3.1所示。现有三种货物待运,已知有相关数据列于表3.2。表3.1项目前舱中舱后舱最大允许载重量(t)200030001500容积(m2)400054001500表3.2商品数量(件)每件体积(m3/件)每件重量(t/件)运价(元/件)A6001081000B100056700C80075600又为了航海安全,前、中、后舱实际载重量大体保持各舱最大允许载重量的比例关系。具1体要求:前、后舱分别与中舱之间载重量比例的偏差不超过15%,前、后舱之间不超过10%。问该货轮应该载A,B,C各多少件运费收入才最大?试建立这个问题的线性规划模型。解:设表示第i件商品在舱j的装载量,i,j=1,2,31)商品的数量约束:2)商品的容积约束:3)最大载重量约束:4)重量比例偏差的约束:5.篮球队需要选择5名队员组成出场阵容参加比赛。8名队员的身高及擅长位置见表5.表5队员12345678身高(m)1.921.91.881.861.851.831.81.78擅长位置中锋中锋前锋前锋前锋后卫后卫后卫出场阵容应满足以下条件:(1)只能有一名中锋上场;(2)至少一名后卫;(3)如1号和4号均上场,则6号不出场;(4)2号和8号至少有一个不出场。问应当选择哪5名队员上场,才能使出场队员平均身高最高,试建立数学模型。2解:设表示第i个队员出场,i=1,2…8.6.时代服装公司生产一款新的时装,据预测今后6个月的需求量如表4所示,每件时装用工2h和10元原材料费,售价40元。该公司1月初有4名工人,每人每月可工作200h,月薪2000元。该公司可于任一个月初新雇工人,但每雇1人需一次性额外支出1500元,也可辞退工人,但每辞退1人需补偿1000元。如当月生产数超过需求,可留到后面月份销售,但需付库存费每件每月5元,当供不应求时,短缺数不需补上。试帮组该公司决策,如何使用6个月的总利润最大。表4单位:件月份123456需求500600300400500800解:设为第i月现有工人人数,为新雇工人人数,为辞退工人人数,为每月的需求。i=1,2,…,6。则有:7.童心玩具厂下一年度的现金流(万元)如表6所示,表中负号表示该月现金流出大于流入,为此该厂需借款。借款有两种方式:一是于上一年末借一年期贷款,一次得全部贷款额,从1月底起每月还息1%,于12月归还本金和最后一次利息;二是得到短期贷款,每月初获得,于月底归还,月息1.5%。当该厂有多余现金时,可短期存款,月初存入,月末取出,月息0.4%。问该厂应如何进行存贷款操作,既能弥补可能出现的负现金流,又可使年末现金总量为最大。表6月份123456789101112现金流-12-10-8-10-45-7-21512-745解:设长期存款为y,为第i个月的短期贷款额,为第i个月短期存款额,i=1,2,3…,n。则有:8.某地准备投资D元建民用住宅,可以建住宅的...