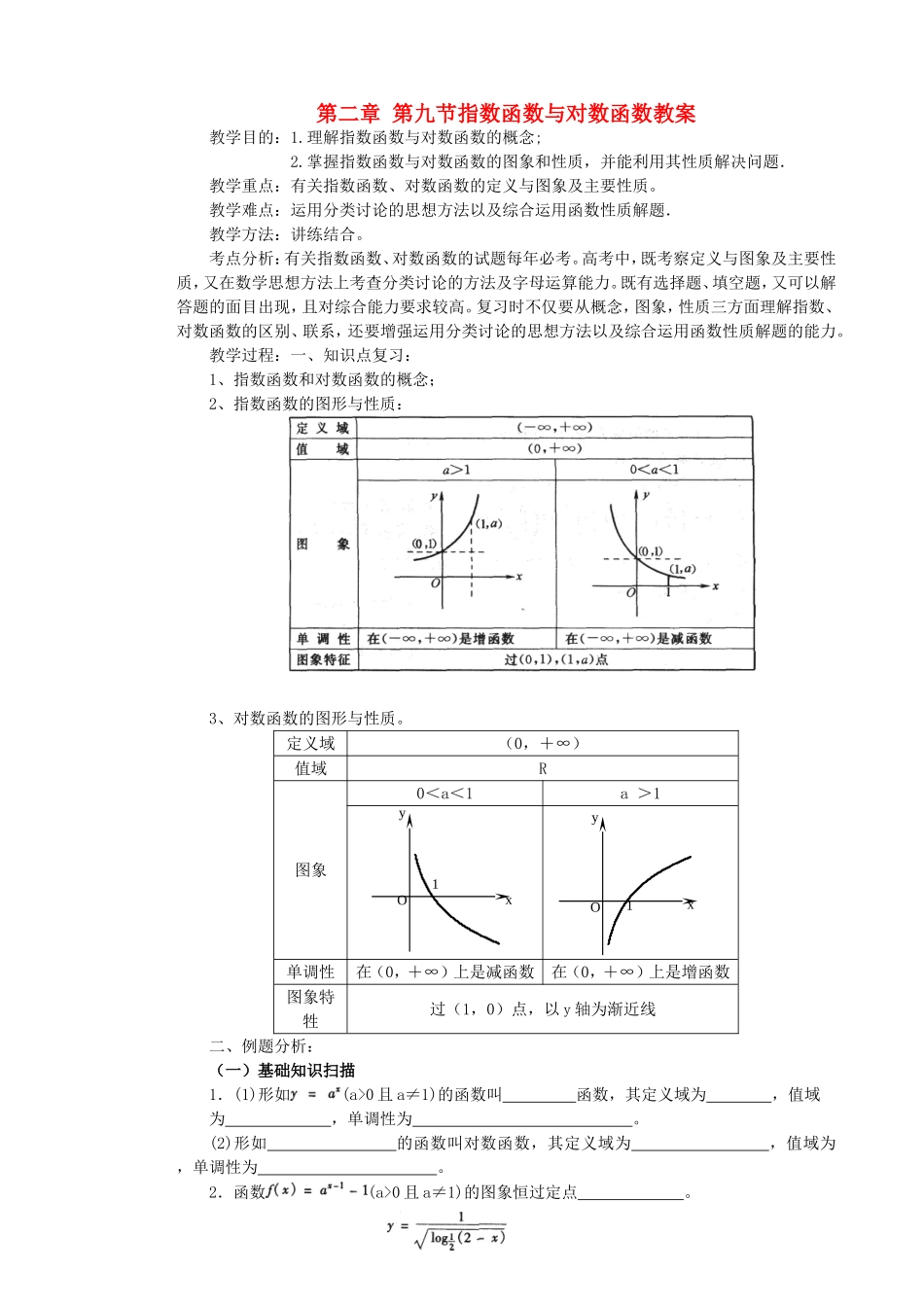
第二章第九节指数函数与对数函数教案教学目的:1.理解指数函数与对数函数的概念;2.掌握指数函数与对数函数的图象和性质,并能利用其性质解决问题.教学重点:有关指数函数、对数函数的定义与图象及主要性质。教学难点:运用分类讨论的思想方法以及综合运用函数性质解题.教学方法:讲练结合。考点分析:有关指数函数、对数函数的试题每年必考。高考中,既考察定义与图象及主要性质,又在数学思想方法上考查分类讨论的方法及字母运算能力。既有选择题、填空题,又可以解答题的面目出现,且对综合能力要求较高。复习时不仅要从概念,图象,性质三方面理解指数、对数函数的区别、联系,还要增强运用分类讨论的思想方法以及综合运用函数性质解题的能力。教学过程:一、知识点复习:1、指数函数和对数函数的概念;2、指数函数的图形与性质:3、对数函数的图形与性质。定义域(0,+∞)值域R图象0<a<1a>1单调性在(0,+∞)上是减函数在(0,+∞)上是增函数图象特牲过(1,0)点,以y轴为渐近线二、例题分析:(一)基础知识扫描1.(1)形如(a>0且a≠1)的函数叫函数,其定义域为,值域为,单调性为。(2)形如的函数叫对数函数,其定义域为,值域为,单调性为。2.函数(a>0且a≠1)的图象恒过定点。yOx1xyO13.(1996年上海市)函数的定义域是.4.的值域为.5.,,,这三数用“<”号连结后得.6.图中的曲线是对数函数y=的图象.已知a取,,,四个值,则相应于曲线c1、c2、c3、c4的a值依次为()A.B.C.D.(二)题型分析:题型1:指数、对数函数的图象和性质例1求下列函数的定义域、值域、单调区间.(1)(2)例2.已知函数(a>0,b>0,a≠1).(1)求的定义域;(2)讨论的奇偶性;(3)讨论的单调性;(4)求的反函数分析利用函数的性质,并结合对数函数的知识求解.注意:(1)用定义判断函数的奇偶性时,应注意隐含的条件:定义域所在区间应关于原点对称.(2)注意对底数a的分类讨论.此例在讨论单调性时,不能认为f(x)的单调区间是(-∞,-b)∪(b,+∞).题型2:指数、对数函数性质的应用.例3比较下列各组中两个数的大小,并说明理由.(1),(2)与(3)三个数,,的大小顺序是()A.B.C.D.分析利用指、对数函数的单调性比较大小.(1)由于这两个数的底数不同,指数也不同,所以可利用中间量来区分它们的大小,注意到这两个数的特点,中间量应为或(2)注意到两个对数的真数相同,可先比较与的大小.对于第(2)小题,也可以利用对数函数的图象,当底数大于1时,底数越大,在直线x=1左侧图象越靠近x轴,由下图所示可得例4(北京、安徽春季高考题)设函数,若0
0,b>0),求使y为负值的x的取值范围.分析欲求使y<0的x的取值范围.需将进行等价转化!如何转化?要重视分类讨论思想的掌握和运用,它是高考考查热点之一.三、本节所涉及的数学思想·规律·方法小结:1.指数函数的底数及对数函数的真数和底数应满足的条件,是求解有关指数,对数问题时必须予以特别重视的.2.研究指数、对数问题尽量化为同底,另外,对数问题中要重视定义域的限制.3.要充分利用指数函数和对数函数的概念、图象、性质讨论一些复合函数的性质.四、作业:《纸上练兵》P64—65五、课后记: