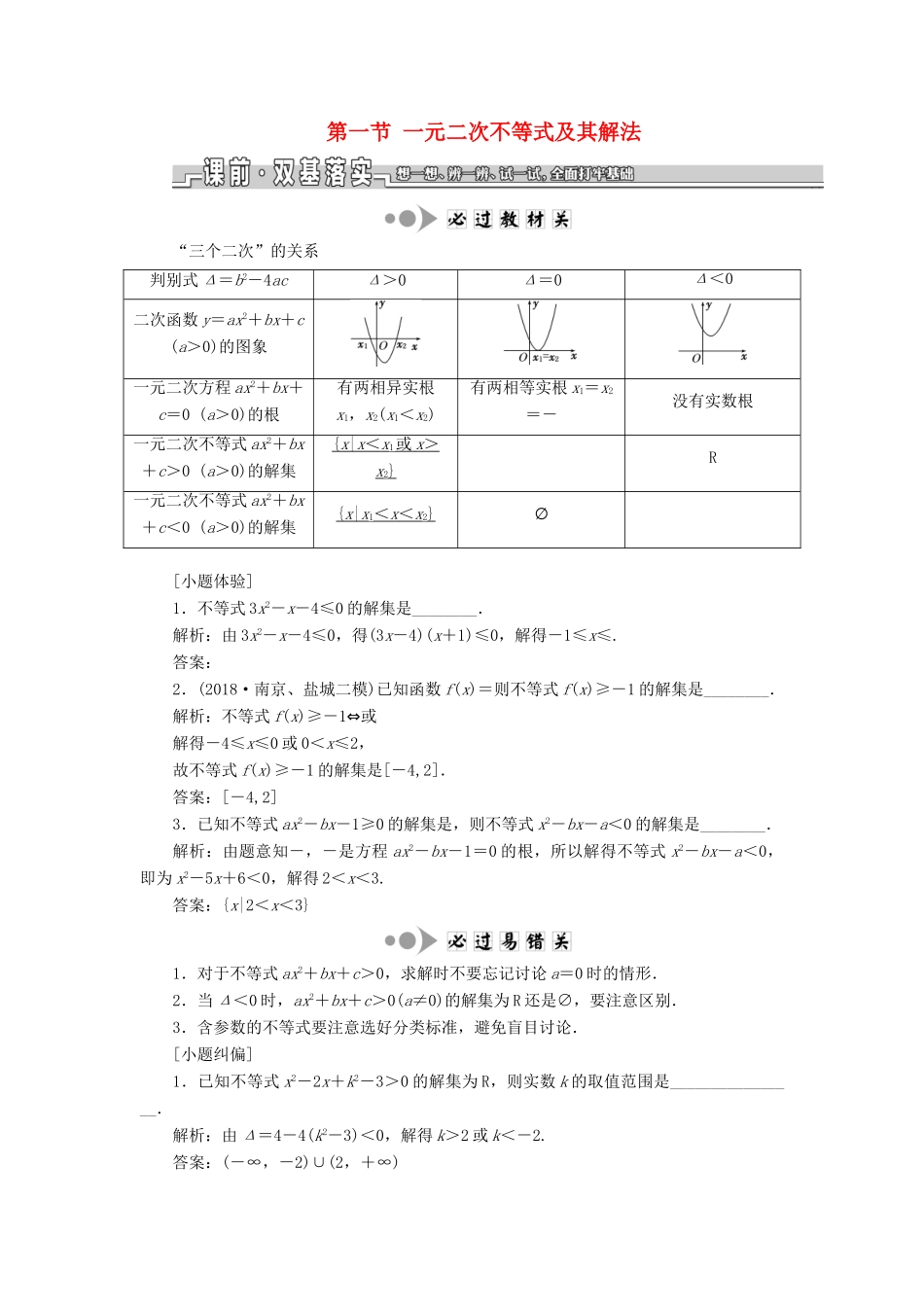
第一节一元二次不等式及其解法“三个二次”的关系判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图象一元二次方程ax2+bx+c=0(a>0)的根有两相异实根x1,x2(x1<x2)有两相等实根x1=x2=-没有实数根一元二次不等式ax2+bx+c>0(a>0)的解集{x|x<x1或x>x2}R一元二次不等式ax2+bx+c<0(a>0)的解集{x|x1<x<x2}∅[小题体验]1.不等式3x2-x-4≤0的解集是________.解析:由3x2-x-4≤0,得(3x-4)(x+1)≤0,解得-1≤x≤.答案:2.(2018·南京、盐城二模)已知函数f(x)=则不等式f(x)≥-1的解集是________.解析:不等式f(x)≥-1⇔或解得-4≤x≤0或0<x≤2,故不等式f(x)≥-1的解集是[-4,2].答案:[-4,2]3.已知不等式ax2-bx-1≥0的解集是,则不等式x2-bx-a<0的解集是________.解析:由题意知-,-是方程ax2-bx-1=0的根,所以解得不等式x2-bx-a<0,即为x2-5x+6<0,解得2<x<3.答案:{x|2<x<3}1.对于不等式ax2+bx+c>0,求解时不要忘记讨论a=0时的情形.2.当Δ<0时,ax2+bx+c>0(a≠0)的解集为R还是∅,要注意区别.3.含参数的不等式要注意选好分类标准,避免盲目讨论.[小题纠偏]1.已知不等式x2-2x+k2-3>0的解集为R,则实数k的取值范围是________________.解析:由Δ=4-4(k2-3)<0,解得k>2或k<-2.答案:(-∞,-2)∪(2,+∞)2.若不等式(a-2)x2+2(a-2)x-4<0对x∈R恒成立,则实数a的取值范围是________.解析:当a-2=0,即a=2时,原不等式为-4<0,所以a=2时成立,当a-2≠0,即a≠2时,由题意得即解得-2<a<2.综上所述,-2<a≤2.答案:(-2,2][题组练透]1.(2018·南通中学检测)不等式-3x2+6x>2的解集为________.解析:将不等式-3x2+6x>2转化为3x2-6x+2<0,所以不等式的解集是答案:2.(2019·东湖中学检测)已知函数f(x)=则不等式f(f(x))≤3的解集为________.解析:当x≥0时,f(f(x))=f(-x2)=(-x2)2-2x2≤3,即(x2-3)(x2+1)≤0,解得0≤x≤;当-2<x<0时,f(f(x))=f(x2+2x)=(x2+2x)2+2(x2+2x)≤3,即(x2+2x-1)(x2+2x+3)≤0,即-2<x<0;当x≤-2时,f(f(x))=f(x2+2x)=-(x2+2x)2≤3,解得x≤-2.综上,不等式的解集为{x|x≤}.答案:{x|x≤}3.解下列不等式:(1)(易错题)-3x2-2x+8≥0;(2)0<x2-x-2≤4.解:(1)原不等式可化为3x2+2x-8≤0,即(3x-4)(x+2)≤0.解得-2≤x≤,所以原不等式的解集为.(2)原不等式等价于⇔⇔⇔借助于数轴,如图所示,所以原不等式的解集为.[谨记通法]解一元二次不等式的4个步骤[典例引领](2019·天一中学检测)解关于x的不等式:ax2+(a-2)x-2≥0.解:①当a=0时,原不等式化为x+1≤0,解得x≤-1.②当a>0时,原不等式化为(x+1)≥0,解得x≥或x≤-1.③当a<0时,原不等式化为(x+1)≤0.当>-1,即a<-2时,解得-1≤x≤;当=-1,即a=-2时,解得x=-1;当<-1,即a>-2时,解得≤x≤-1.综上所述,当a=0时,不等式的解集为{x|x≤-1};当a>0时,不等式的解集为;当-2<a<0时,不等式的解集为;当a=-2时,不等式的解集为{x|x=-1};当a<-2时,不等式的解集为.[由题悟法]解含参数的一元二次不等式时分类讨论的依据(1)二次项中若含有参数应讨论是等于0,小于0,还是大于0,然后将不等式转化为一次不等式或二次项系数为正的形式.(2)当不等式对应方程的根的个数不确定时,讨论判别式Δ与0的关系.(3)确定无根时可直接写出解集,确定方程有两个根时,要讨论两根的大小关系,从而确定解集形式.[提醒]当不等式中二次项的系数含有参数时,不要忘记讨论其等于0的情况.[即时应用]1.(2019·苏州实验中学检测)已知x2+px+q<0的解集为,则不等式qx2+px+1>0的解集为________.解析: x2+px+q<0的解集为,∴-,是方程x2+px+q=0的两实数根,则解得∴不等式qx2+px+1>0可化为-x2+x+1>0,即x2-x-6<0,解得-2<x<3,∴不等式qx2+px+1>0的解集为{x|-2<x<3}.答案:{x|-2<x<3}2.求不等式12x2-ax>a2(a∈R)的解集.解:原不等式可化为12x2-ax-a2>0,即(4x+a)(3x-...