山东省郯城县高一数学《对数函数》教案（2）VIP免费

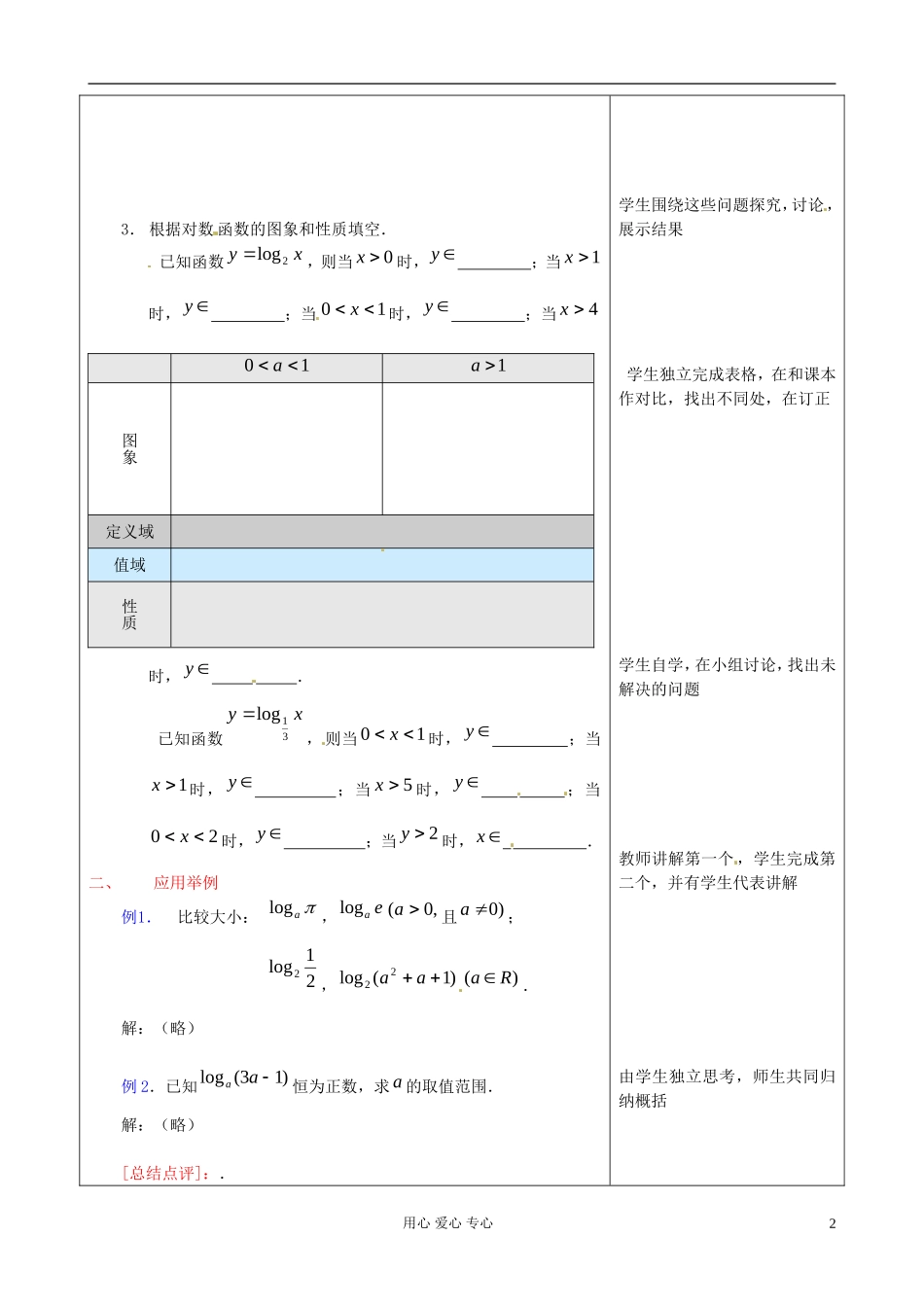
山东省郯城县高一数学《对数函数》教案（2）主备人徐丹课时1年月日分管领导验收结果教学目标（1）进一步理解对数函数的图象和性质；（2）熟练应用对数函数的图象和性质，解决一些综合问题；（3）通过例题和练习的讲解与演练，培养学生分析问题和解决问题的能力．重点对数函数的图象和性质难点对对数函数的性质的综合运用教学过程教师活动学生活动一、回顾与总结1．函数xyxyxylg,log,log52的图象如图所示，回答下列问题．（1）说明哪个函数对应于哪个图象，并解释为什么？（2）函数xyalog与xya1log,0(a且)0a有什么关系？图象之间又有什么特殊的关系？（3）以xyxyxylg,log,log52的图象为基础，在同一坐标系中画出xyxyxy1015121log,log,log的图象．（4）已知函数xyxyxyxyaaaa4321log,log,log,log的图象，则底数之间的关系：．2．完成下表（对数函数xyalog,0(a且)0a的图象和性质）复习回顾对数函数的概念学生动手画图，感受更深刻小组内交流讨论，展示成果用心爱心专心112343．根据对数函数的图象和性质填空．已知函数xy2log，则当0x时，y；当1x时，y；当10x时，y；当4x时，y．已知函数xy31log，则当10x时，y；当1x时，y；当5x时，y；当20x时，y；当2y时，x．二、应用举例例1．比较大小：alog，ealog,0(a且)0a；21log2，)1(log22aa)(Ra．解：（略）例2．已知)13(logaa恒为正数，求a的取值范围．解：（略）[总结点评]：．学生围绕这些问题探究，讨论，展示结果学生独立完成表格，在和课本作对比，找出不同处，在订正学生自学，在小组讨论，找出未解决的问题教师讲解第一个，学生完成第二个，并有学生代表讲解由学生独立思考，师生共同归纳概括用心爱心专心10a1a图象定义域值域性质2．例3．求函数)78lg()(2xxxf的定义域及值域．解：（略）注意：函数值域的求法．例4．（1）函数xyalog在[2，4]上的最大值比最小值大1，求a的值；（2）求函数)106(log23xxy的最小值．解：（略）注意：利用函数单调性求函数最值的方法，复合函数最值的求法．例5．（2003年上海高考题）已知函数xxxxf11log1)(2，求函数)(xf的定义域，并讨论它的奇偶性和单调性．解：（略）注意：判断函数奇偶性和单调性的方法，规范判断函数奇偶性和单调性的步骤．例6．求函数)54(log)(22.0xxyxf的单调区间．解：（略）注意：复合函数单调性的求法及规律：“同增异减”．练习：求函数)23(log221xxy的单调区间．学生找出此类题目的求解规律教师板演第一题，学生代表板演其他，同位之间互批通过这题，你发现了解决这类型题目的规律了吗?学生到黑板展示自己的成果下面学生同位之间互批小结：这节课你有何收获，同位之间相互总结并完善板书设计课题复习引入12概念探究例1例2练习用心爱心专心3用心爱心专心4