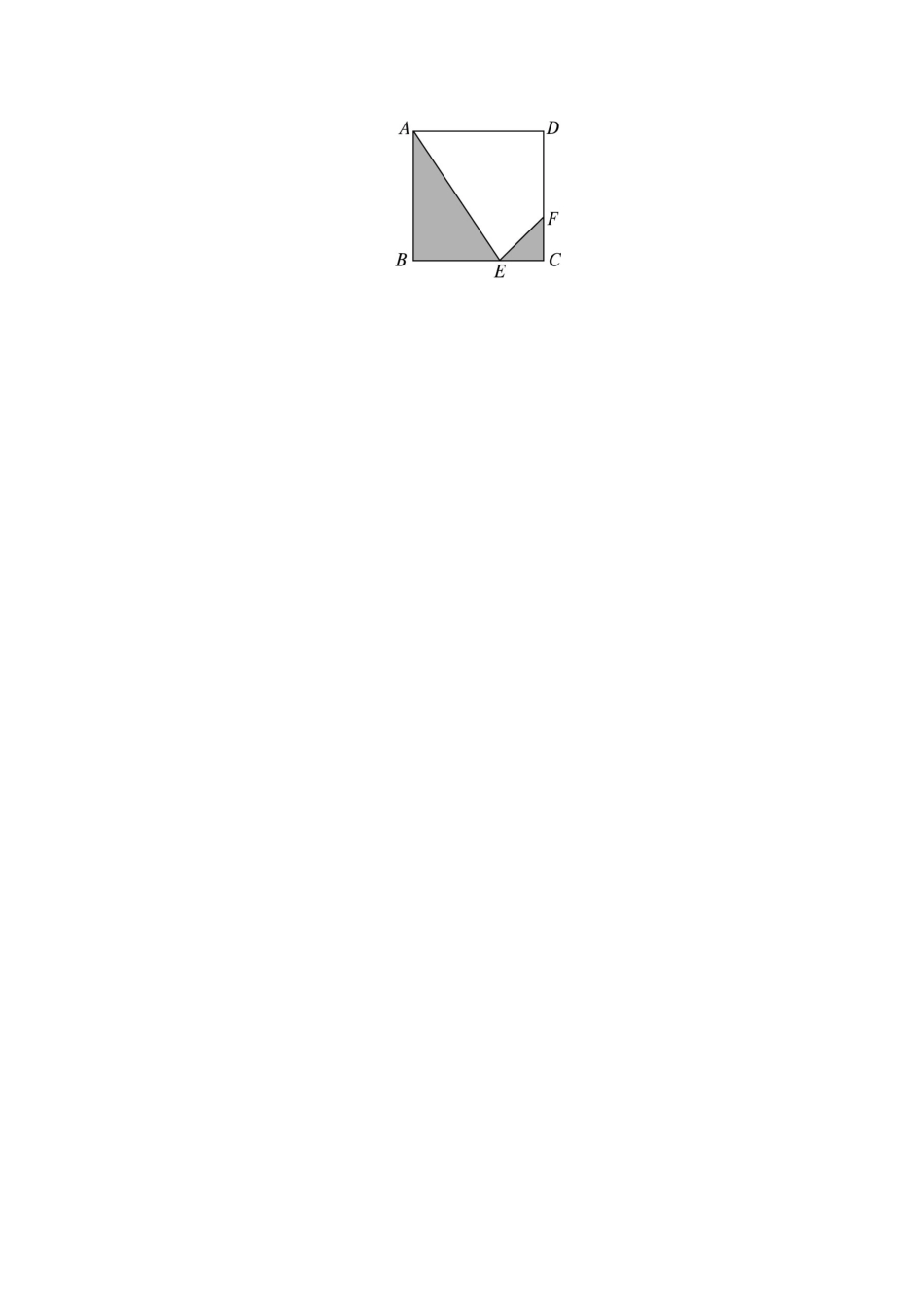
数学湘教必修1第1章集合与函数单元检测(时间:45分钟,满分:100分)一、选择题(本大题共8小题,每小题6分,共48分)1.设集合A={x|x=2k+1,k∈Z},a=5,则有().A.a∈AB.-aAC.{a}∈AD.{a}A2.设全集U={a,b,c,d},A={a,c},B={b},则A∩(UB)=().A.B.{a}C.{c}D.{a,c}3.设集合A={x|1<x<2},B={x|x<a}满足AB,则实数a的取值范围是().A.{a|a≥2}B.{a|a≤1}C.{a|a≥1}D.{a|a≤2}4.若对于任意实数x,都有f(-x)=f(x),且f(x)在(-∞,0]上是递增函数,则().A.f(-2)<f(2)B.f(-1)<C.<f(2)D.f(2)<5.已知函数在区间[1,2]上的最大值为A,最小值为B,则A-B=().A.B.C.1D.-16.设函数f(x)=ax5+bx3+cx+7(a,b,c为常数,x∈R),若f(-7)=-17,则f(7)=().A.31B.17C.-31D.247.已知则f(2)+f(-2)的值为().A.8B.5C.4D.28.函数f(x)=x2-4ax+1在区间[-2,4]上是单调函数的条件是().A.a∈(-∞,-1]B.a∈[2,+∞)C.a∈[-1,2]D.a∈(-∞,-1]∪[2,+∞)二、填空题(本大题共3小题,每小题6分,共18分)9.函数的定义域为__________.10.若集合A={x|ax-1=0},B={x|x2-3x+2=0},且A∪B=B,则a的值是__________.11.若f(x)是定义在R上的奇函数,当x<0时,f(x)=x(1-x),则当x≥0时,函数f(x)的解析式为__________.三、解答题(本大题共3小题,第12、13小题每小题10分,第14小题14分)12.已知函数的定义域为集合A,y=-x2+a2+2a的值域为集合B.(1)若a=2,求A∩B;(2)若A∪B=R,求实数a的取值范围.13.已知函数f(x)的定义域为(-1,1),且同时满足下列条件:(1)f(x)是奇函数;(2)f(x)在定义域上单调递减;(3)f(1-a)+f(1-a2)<0,求a的取值范围.14.某人定制了一批地砖,每块地砖(如图所示)是边长为1米的正方形ABCD,点E,F分别在边BC和CD上,且CE=CF,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元.问点E在什么位置时,每块地砖所需的材料费用最省?参考答案1.答案:A解析:a=5=2×2+1,2∈Z,所以a∈A,故选A.2.答案:D解析:因为全集U={a,b,c,d},B={b},所以UB={a,c,d},于是A∩(UB)={a,c},故选D.3.答案:A解析:根据已知条件画出数轴可知选A.4.答案:D解析:由题意知f(x)是R上的偶函数,且在[0,+∞)上是递减函数,所以有f(-2)=f(2),f(-1)=f(1)>,=>f(2),故选D.5.答案:A解析:因为f(x)=在区间[1,2]上单调递减,所以f(1)=A,f(2)=B.所以A-B=f(1)-f(2)=1-=,故选A.6.答案:A解析:因为f(-7)=a(-7)5+b(-7)3+c(-7)+7=-17,所以a(-7)5+b(-7)3+c(-7)=-24.所以a·75+b·73+c·7=24.所以有f(7)=a·75+b·73+c·7+7=31,故选A.7.答案:B解析:依题意f(2)=22=4,f(-2)=f(-2+1)=f(-1)=f(-1+1)=f(0)=f(0+1)=f(1)=1,所以f(2)+f(-2)=5,选B.8.答案:D解析:由于f(x)=x2-4ax+1=(x-2a)2+1-4a2,所以函数图象的对称轴是直线x=2a,要使函数在区间[-2,4]上是单调函数,必须满足2a≤-2或2a≥4,解得a≤-1或a≥2,故选D.9.答案:{x|x≥-4且x≠1}解析:要使函数有意义,应满足解得x≥-4且x≠1,故函数定义域为{x|x≥-4且x≠1}.10.答案:0,1,解析:由A∪B=B得AB,而B={x|x2-3x+2=0}={1,2}.当a=0时A=,符合要求;当a≠0时,应有或,所以a=1或,因此实数a的值等于0,1,.11.答案:f(x)=x(1+x)解析:设x>0,则-x<0,所以f(-x)=-f(x)=-x(1+x),所以f(x)=x(1+x).又因为f(0)=0,所以当x≥0时,f(x)=x(1+x).12.解:依题意,整理得A={x|x>3},B={y|y≤a2+2a},(1)当a=2时,B={y|y≤8},所以A∩B=(3,8];(2)分析易知,要使A∪B=R,需要a2+2a>3,解得a≤-3或a≥1.13.解:由题意,得f(1-a)<-f(1-a2)=f(a2-1),则解得0<a<1.所以a的取值范围是(0,1).14.解:设CE=x,则BE=1-x,每块地砖的费用为W,且制成△CFE,△ABE和四边形AEFD三种材料的每平方米价格依次为30元、20元、10元.则W=x2·30+×1×(1-x)×20+×10=10x2-5x+15=.当x==0.25(米)时,W有最小值,即费用最省.答:当点E在距点C为0.25米时,每块地砖所需费用最省.