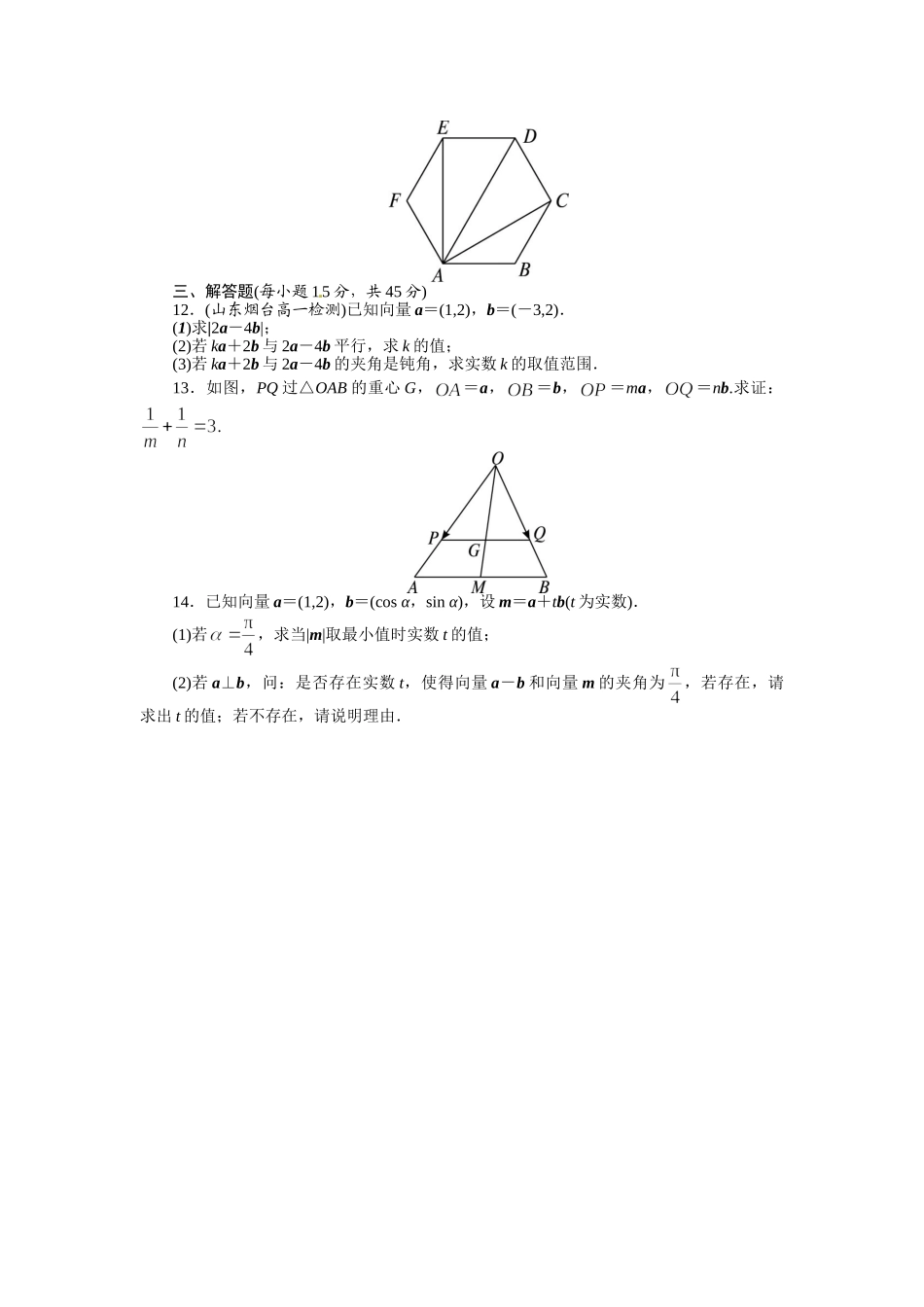
数学湘教版必修2第4章向量单元检测(时间:45分钟满分:100分)一、选择题(每小题5分,共40分)1.(浙江台州高一期末检测)下列向量是单位向量的是()A.a=B.a=(1,1)C.a=(1,sinα)D.a=(cosα,sinα)2.已知a=(-5,6),b=(-3,2),c=(x,y),若a-3b+2c=0,则c等于()A.(-2,6)B.(-4,0)C.(7,6)D.(-2,0)3.在△ABC中,AB=5,BC=2,∠B=60°,则·的值为()A.B.5C.D.-54.(山东兖州高一模拟)已知向量a=(sinθ,cosθ-2sinθ),b=(1,-3),若a∥b,则tanθ的值等于()A.B.C.-1D.15.已知D是△ABC所在平面内一点,=+,则()A.=B.=C.=D.=6.(山东潍坊高一期中检测)对于向量a,b,e及实数x,y,x1,x2,λ,给出下列四个条件:①a+b=3e且a-b=5e;②x1a+x2b=0;③a=λb(b≠0)且λ唯一;④xa+yb=0(x+y=0).其中能使a与b共线的是()A.①②B.②④C.①③D.③④7.(辽宁大连高一期末检测)设a=(-3,m),b=(4,3),若a与b的夹角是钝角,则实数m的取值范围是()A.m≠4且B.m<4且C.m>4D.m<48.过点M(3,0)的直线交圆x2+y2-4x=0于A,B两点,C为圆心,则·的最大值等于()A.B.C.2D.-2二、填空题(每小题5分,共15分)9.(江苏灌云高一检测)已知向量a=(1,n),b=(-1,n),若2a-b与b垂直,则|a|=__________.10.已知定义|a×b|=|a||b|·sinθ,其中θ为向量a与b的夹角.若|a|=2,|b|=3,a·b=-4,则|a×b|=__________.11.(福建师大附中高一检测)如图,在正六边形ABCDEF中,有下列三个命题:①+=2;②=2+2;③·=·.其中真命题的序号是__________.(写出所有真命题的序号)三、解答题(每小题15分,共45分)12.(山东烟台高一检测)已知向量a=(1,2),b=(-3,2).(1)求|2a-4b|;(2)若ka+2b与2a-4b平行,求k的值;(3)若ka+2b与2a-4b的夹角是钝角,求实数k的取值范围.13.如图,PQ过△OAB的重心G,=a,=b,=ma,=nb.求证:.14.已知向量a=(1,2),b=(cosα,sinα),设m=a+tb(t为实数).(1)若,求当|m|取最小值时实数t的值;(2)若a⊥b,问:是否存在实数t,使得向量a-b和向量m的夹角为,若存在,请求出t的值;若不存在,请说明理由.参考答案1.答案:D解析:只有在D项中,|a|==1,是单位向量.2.答案:D解析:依题意得c=a+b=(-5,6)+(-3,2)=(-2,0).3.答案:D解析:·=||·||cos〈·〉=5×2×cos120°=-5.4.答案:C解析:由a∥b得-3sinθ=cosθ-2sinθ,于是-sinθ=cosθ,故tanθ==-1.5.答案:A解析:由=+,得+=+,因此-=-,所以=,即=.6.答案:C解析:由a+b=3e和a-b=5e可得a=4e,b=-e,显然a与b共线,故①正确;③显然正确,故选C.7.答案:B解析:因为a与b的夹角是钝角,所以a·b<0,即3m-12<0,解得m<4,但当a与b共线时,有-9=4m,解得,且这时a与b反向共线,夹角是π,不合题意,故实数m的取值范围是m<4且.8.答案:D解析:由已知得圆的半径为2,圆心坐标为(2,0),所以·=·=2×2×cos∠ACB.因为直线过点M(3,0),所以当该直线与CM垂直时,∠ACB最小,等于120°,这时cos∠ACB取到最大值,所以·的最大值等于2×2×=-2.9.答案:2解析:依题意2a-b=(3,n),由于2a-b与b垂直,所以-3+n2=0,解得n2=3,于是|a|==2.10.答案:解析:由于a·b=|a|·|b|cosθ,所以.又θ∈[0,π],于是,故|a×b|=|a||b|sinθ=2×3×=.11.答案:①②解析:由于+==2,所以①正确;设正六边形中心为O,则=2=2(+),即=2+2,所以②正确;由于·-·=·(-)=·=2||2>0,所以不可能有·=·,故③错误.12.解:(1)∵2a-4b=(14,-4),∴|2a-4b|=.(2)∵ka+2b=(k-6,2k+4),且ka+2b与2a-4b平行,∴14(2k+4)+4(k-6)=0,即32k+32=0,∴k=-1.(3)∵ka+2b与2a-4b的夹角是钝角,∴(ka+2b)·(2a-4b)<0且k≠-1,即14(k-6)-4(2k+4)<0且k≠-1,∴且k≠-1.13.证明:∵M是AB边的中点,∴=(+)=(a+b).∴==·(a+b)=a+b.∴=-=nb-ma,=-=a+b.∵∥,∴.整理得mn=(m+n),即.14.解:(1)因为,b=,a·b=,则=,所以当时,|m|取到最小值,最小值为.(2)由条件得,又因为|a-b|=,|a+tb|=,(a-b)·(a+tb)=5-t,则有,且t<5,整理得t2+5t-5=0,所以存在满足条件.