苏教版必修5高中数学一元二次不等式2VIP免费

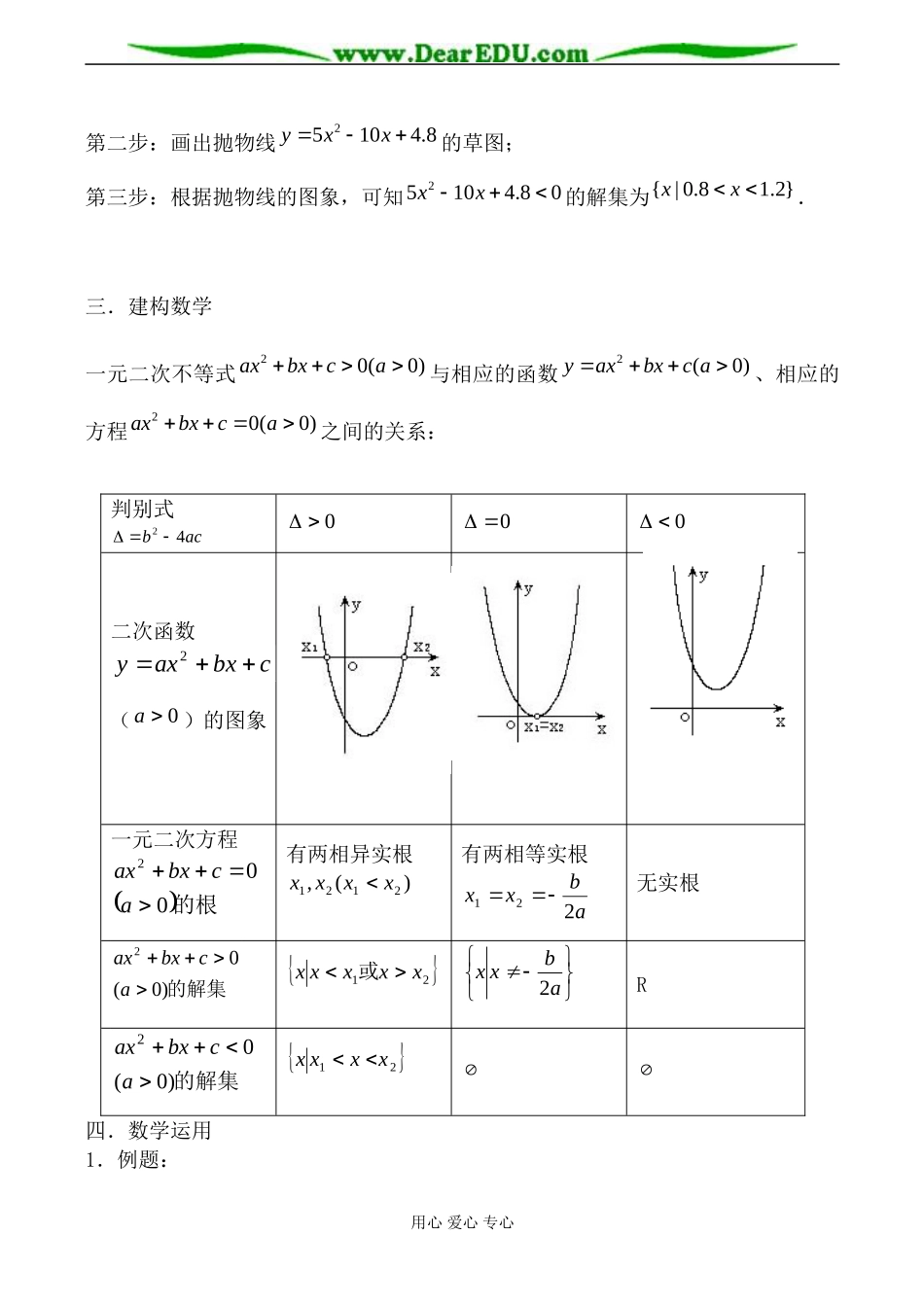
一元二次不等式教学目标（1）通过函数图象了解一元二次不等式与对应函数、方程的联系；（2）会解一元二次不等式，对给定的一元二次不等式，尝试设计求解的程序框图；（3）掌握利用因式分解和讨论来求解一元二次不等式的方法及这种方法的推广运用；（4）掌握将分式不等式转化为一元二次不等式求解．教学重点，难点弄清一元二次方程、一元二次不等式及二次函数三者之间的关系，掌握一元二次不等式的解法，学会将分式不等式转化为一元二次不等式求解．教学过程一．问题情境在上节问题（2）中，我们得到不等式25104.80xx，像这样只含有一个未知数，并且未知数最高次数是2的不等式叫做一元二次不等式．我们知道，一元二次方程和相应的二次函数有着密切的联系，一元二次方程的根就是相应二次函数的图象与x轴交点的横坐标．那么，一元二次不等式和对应的二次函数是否也有内在的联系？下面先让我们考虑这样一个问题：当x是什么实数时，函数25104.8yxx的值是：（1）0；（2）正数；（3）负数．二．学生活动观察函数25104.8yxx的图象，可以看出，一元二次不等式25104.80xx的解集就是二次函数25104.8yxx的图象（抛物线）位于x轴下方的点所对应的x值的集合．因此，求解一元二次不等式可以先解相应的一元二次方程，确定抛物线与x轴交点的横坐标，再根据图象写出不等式的解集．第一步：解方程25104.80xx，得120.8,1.2xx；用心爱心专心第二步：画出抛物线25104.8yxx的草图；第三步：根据抛物线的图象，可知25104.80xx的解集为{|0.81.2}xx．三．建构数学一元二次不等式20(0)axbxca与相应的函数2(0)yaxbxca、相应的方程20(0)axbxca之间的关系：判别式acb42000二次函数cbxaxy2（0a）的图象一元二次方程的根002acbxax有两相异实根)(,2121xxxx有两相等实根abxx221无实根的解集)0(02acbxax21xxxxx或abxx2R的解集)0(02acbxax21xxxx四．数学运用1．例题：用心爱心专心解下列不等式：(1)27120xx；(2)2230xx；(3)2210xx；(4)2220xx．解：(1)方程27120xx的解为123,4xx．根据2712yxx的图象，可得原不等式27120xx的解集是{|34}xxx或．(2)不等式两边同乘以1，原不等式可化为2230xx．方程2230xx的解为123,1xx．根据223yxx的图象，可得原不等式2230xx的解集是{|31}xx．(3)方程2210xx有两个相同的解121xx．根据221yxx的图象，可得原不等式2210xx的解集为．(4)因为0，所以方程2220xx无实数解，根据222yxx的图象，可得原不等式2220xx的解集为．归纳解一元二次不等式的步骤：（1）二次项系数化为正数；（2）解对应的一元二次方程；（3）根据一元二次方程的根，结合不等号的方向画图；（4）写出不等式的解集．用心爱心专心思考：（1）求解一元二次不等式20(0)axbxca的过程，怎样用流程图来描述（2）求解一元二次不等式20(0)axbxca的过程，怎样用流程图来描述？(3)不等式20(0)axbxca和20(0)axbxca的解法？说明：对于例1（１），还可将其转化为一次不等式（组）来求解，这种求法不仅体现了化归思想，而且更有一般性．例2.（1）解不等式073xx；（若改为307xx呢？）（2）解不等式2317xx；（3）解不等式2202xxx．(若改为：01122xxx如何？)解:(1)原不等式03,0703,07xxxx或{|73}xx({|73}xx)(2)1007xx即{|710}xx(3)分析：根据实数运算的符号法则，可以化为不等式组求解.原不等式的解集是下面两个不等式组解集的并集：(1);01,0122xxx(2).01,0122xxx用心爱心专心(1)12;(2)121.xx解得解得所以原不等式的解集是{|121xx或12}x．说明：本题是将一个比较复杂的不等式转化为不等式组进行求解，在解的过程...