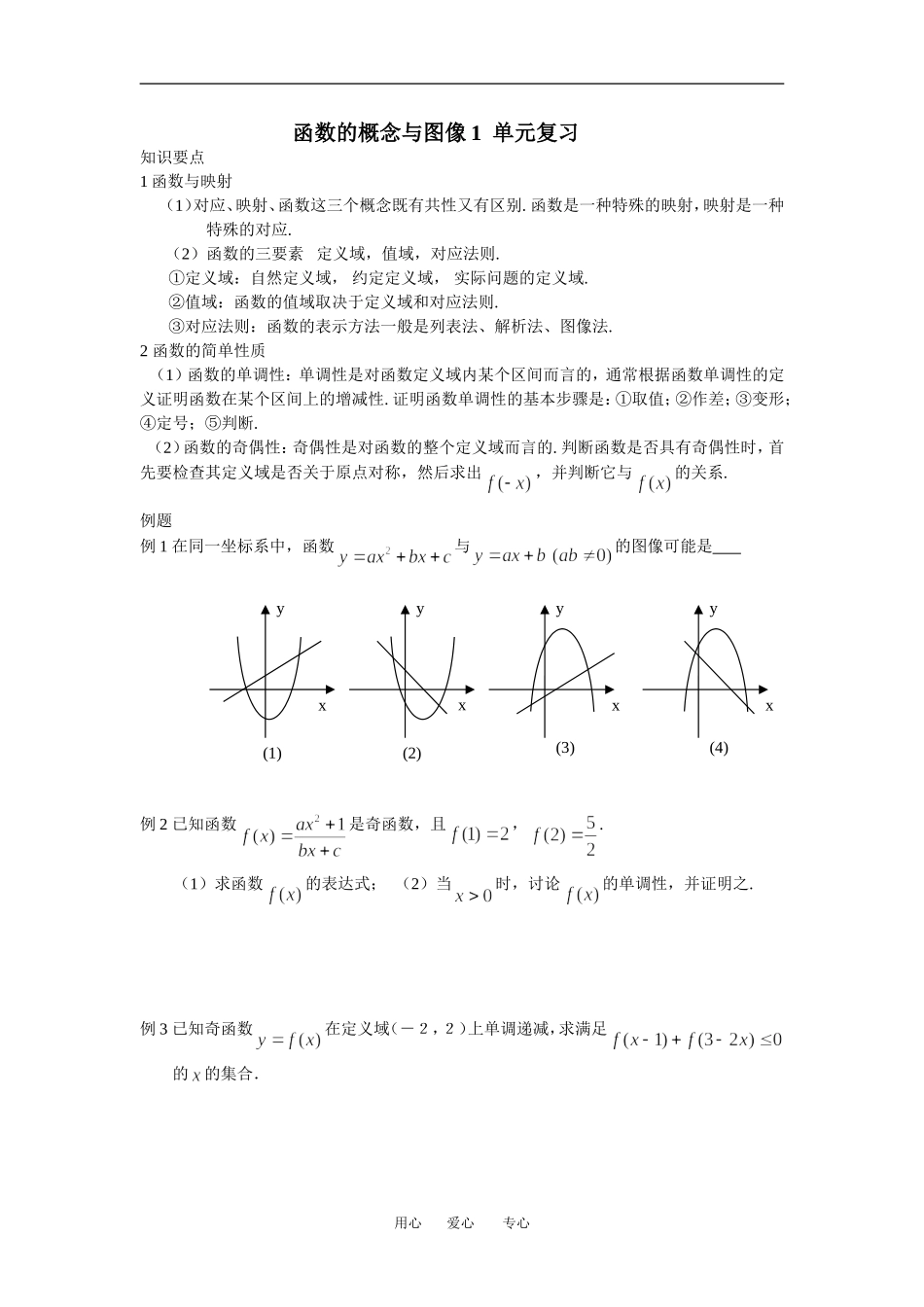
函数的概念与图像1单元复习知识要点1函数与映射(1)对应、映射、函数这三个概念既有共性又有区别.函数是一种特殊的映射,映射是一种特殊的对应.(2)函数的三要素定义域,值域,对应法则.①定义域:自然定义域,约定定义域,实际问题的定义域.②值域:函数的值域取决于定义域和对应法则.③对应法则:函数的表示方法一般是列表法、解析法、图像法.2函数的简单性质(1)函数的单调性:单调性是对函数定义域内某个区间而言的,通常根据函数单调性的定义证明函数在某个区间上的增减性.证明函数单调性的基本步骤是:①取值;②作差;③变形;④定号;⑤判断.(2)函数的奇偶性:奇偶性是对函数的整个定义域而言的.判断函数是否具有奇偶性时,首先要检查其定义域是否关于原点对称,然后求出,并判断它与的关系.例题例1在同一坐标系中,函数与的图像可能是例2已知函数是奇函数,且,.(1)求函数的表达式;(2)当时,讨论的单调性,并证明之.例3已知奇函数在定义域(-2,2)上单调递减,求满足的的集合.用心爱心专心xxxxyyyy(3)(4)(1)(2)作业1.已知函数,则=2.已知是二次函数,且,则3.已知函数满足,且,则实数4.已知的定义域为,则函数的定义域为5.已知函数在定义域R上是单调递减函数,且,则=6.已知函数是偶函数,则实数7.已知函数是R上的奇函数,且时,.则8.函数的定义域是9.已知函数,则10.判断函数在区间上的单调性.并证明你的结论.11.函数的定义域为R,且对于任意均满足,若时,,且(1)证明:是奇函数;(2)求在[-3,3]上的最大值和最小值.用心爱心专心