江西乐安一中高二数学 教案15 椭圆VIP免费

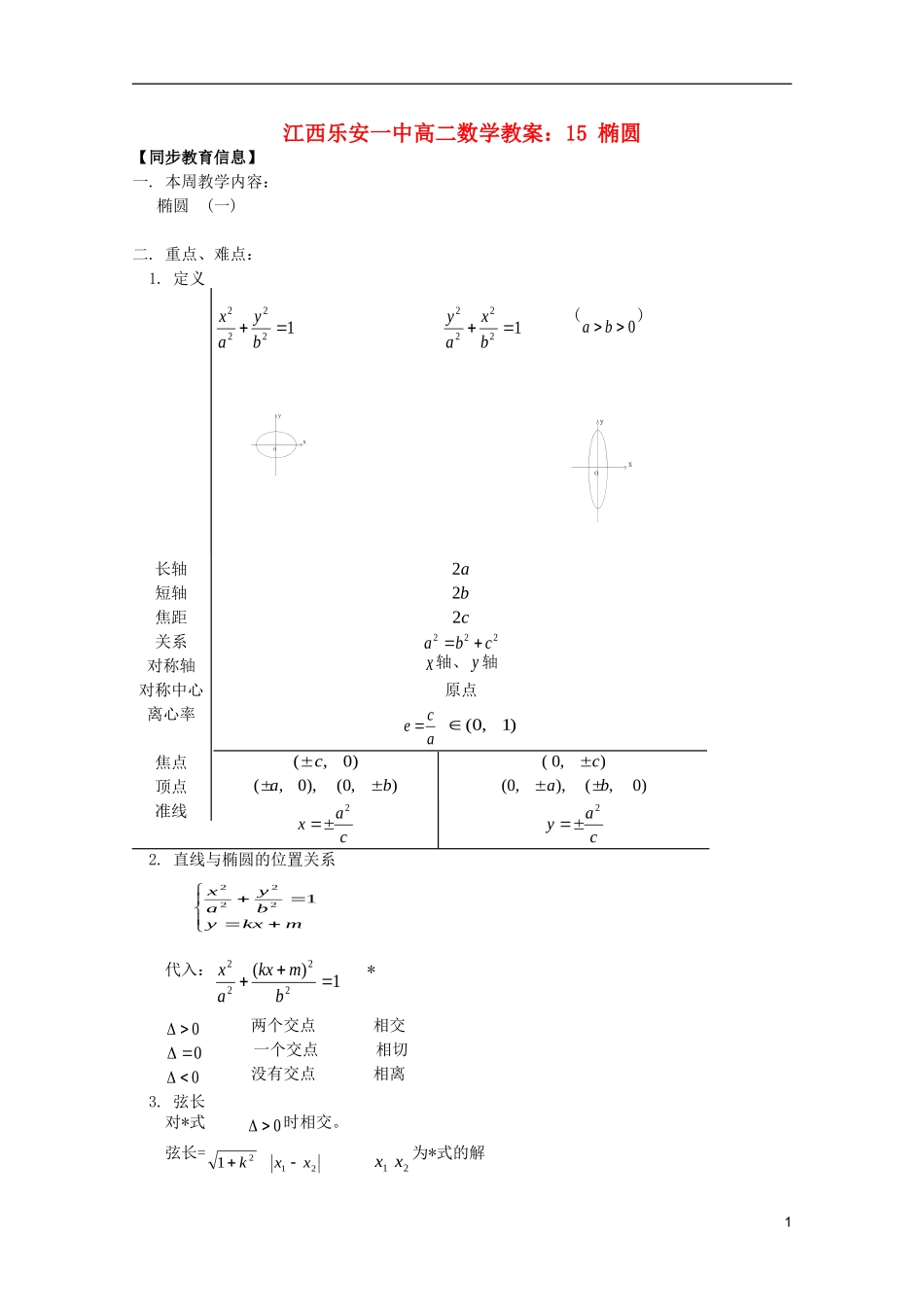
江西乐安一中高二数学教案：15椭圆【同步教育信息】一.本周教学内容：椭圆(一)二.重点、难点：1.定义12222byax12222bxay(0ba)yxoyxo长轴a2短轴b2焦距c2关系222cba对称轴x轴、y轴对称中心原点离心率ace)1,0(焦点)0,(c),0(c顶点),0(),0,(ba)0,(),,0(ba准线cax2cay22.直线与椭圆的位置关系mkxybyax12222代入：1)(2222bmkxax*0两个交点相交0一个交点相切0没有交点相离3.弦长对*式0时相交。弦长=2121xxk21xx为*式的解14.中点弦公式),(00yxP为椭圆12222byax内一点。过P的直线交椭圆于A、B。P恒为AB中点则有：0022yxabKAB证：设),(11yxA),(22yxBP为AB中点。0212xxx0212yyyA、B在椭圆上：1221221byax1222222byax相减0))(())((2212122121byyyyaxxxx2121222121yyxxabxxyy【典型例题】一.椭圆的方程[例1]求焦点为（3，0）（－3,0），离心率31e的椭圆3c9a26b1278122yx[例2]求中心在原点，两准线间距离为5。焦距为4的椭圆方程。522ca2c15ba1522yx或1522xy[例3]求中心在原点，焦点在x轴，椭圆上点M（8，12）到左焦点距离为20的椭圆方程。∵2222012)8(c816)8(22cc1212)88(22163212202aa2119225622yx[例4]求以椭圆364922yx的长轴端点为短轴端点,且过点(－4,1)的椭圆标准方程.19222yax（－4，1）代入182a191822yx[例5]求椭圆14922yx共焦点的且过M（3，－2）的椭圆方程。51492222baba101522ba1101522yx二.直线与椭圆[例1]直线mxy与椭圆191622yx的交点的个数，并求最大弦长。解：mxyyx1916220)9(16322522mmxx)25(9642m（1）5m时，只有一个焦点（2）),5()5,(m没有焦点（3）)5,5(m时有两个焦点A、B212212212214)(2)()(xxxxyyxxAB时02252432582)25(9)25(64225)9(64)2532(22222mmmm[例2]已知椭圆141622yx，M（1，1）在椭圆内求M为中点的椭圆的弦AB的直线方程。解：设),(),(2211yxByxA222121yyxx14162121yx314162222yx相减04))((16))((21212121yyyyxxxx)(42121yyxx412121xxyyABl：)1(411xy054yx三.面积与角度[例1]P椭圆12222byax一点（不在x轴上）21FF为焦点，21PFF求21PFFS。解：221222142aPFPFPFPF22122214cos2cPFPFPFPF相减2214)cos1(2bPFPFcos12221bPFPF2tansin2122121bPFPFSPFF[例2]椭圆12222byax（0ba）的长轴的两焦点为A、B若椭圆上存在一点P使120APB求椭圆离心率e的取值范围。解：在短轴顶点取得最大值。)(3360tan2222cababa)1,36[32322222eacca),(00yxP为椭圆上一点。PAPBPAPBkkkkAPB1tan4)1(22122200220200220200000bayayayxayaxyaxyaxy0222022012ycabycbay只研究第一象限],0(0by随0y变大APBtan为负且变大。APB变大。【模拟试题】一.选择题：1.椭圆192522yx上有一点P到左准线的距离为25则P到椭圆右焦点的距离为（）A.8B.265C.29D.8152.若方程aaxy31lg22表示焦点在x轴上的椭圆则a的取值范围是（）A.（31,0）B.),31(C.)101,0(D.)31,101(3.若方程12sinsin22yx表示椭圆，则的取值范围是（）A.（2,kk）ZkB.（22,2kk）ZkC.)42,2(kkZkD.以上皆不正确二.填空：4.若直线1kxy（RK）与椭圆1522myx恒有公共点则m的取值范围是5.xy1交椭圆122nymx于M、N，MN中点为P若22OPk（O为原点）则nm6.椭圆：9922yx交直线l：022yx于A、B，则AB=56【试题答案】一.选择题：1.A2.D3.D二.填空：4.),5()5,1[5.2/26.2.17