湖南省蓝山二中高中数学《2.3 变量间的相互关系复习课》教案 新人教A版必修3VIP免费

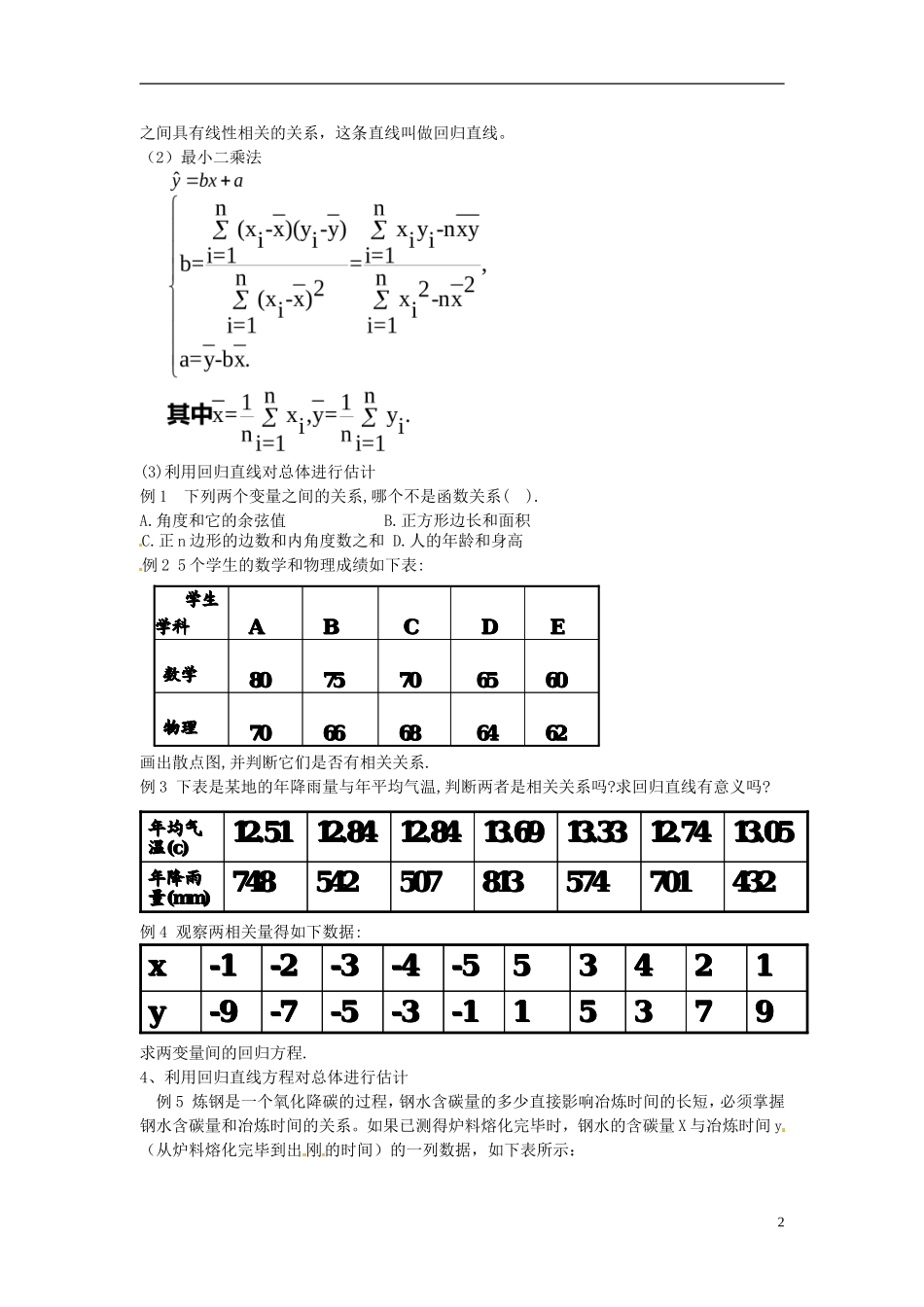
湖南省蓝山二中高一数学《2.3变量间的相互关系复习课》教案新人教A版必修3教学目标：1.通过实例体会变量间的相互关系的意义和作用;2.通过收集现实问题中两个有关联变量的数据作出散点图，并利用散点图直观认识变量间的相关关系；3.知道最小二乘法的思想，能根据给出的线性回归方程系数公式建立线性回归方程。重点与难点重点：作出散点图和根据给出的线性回归方程系数公式建立线性回归方程。难点：对最小二乘法的理解。重点知识回顾1、相关关系（1）概念：自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫相关关系。（2）相关关系与函数关系的异同点。相同点：两者均是指两个变量间的关系。不同点：函数关系是一种确定关系，是一种因果系；相关关系是一种非确定的关系，也不一定是因果关系（但可能是伴随关系）。（3）相关关系的分析方向。在收集大量数据的基础上，利用统计分析，发现规律，对它们的关系作出判断。2、两个变量的线性相关（1）回归分析对具有相关关系的两个变量进行统计分析的方法叫回归分析。通俗地讲，回归分析是寻找相关关系中非确定关系的某种确定性。（2）散点图A、定义；B、正相关、负相关。3、回归直线方程注:如果关于两个变量统计数据的散点图呈现发散状,则这两个变量之间不具有相关关系.（1）回归直线：观察散点图的特征，如果各点大致分布在一条直线的附近，就称两个变量1之间具有线性相关的关系，这条直线叫做回归直线。（2）最小二乘法(3)利用回归直线对总体进行估计例1下列两个变量之间的关系,哪个不是函数关系().A.角度和它的余弦值B.正方形边长和面积C.正n边形的边数和内角度数之和D.人的年龄和身高例25个学生的数学和物理成绩如下表:画出散点图,并判断它们是否有相关关系.例3下表是某地的年降雨量与年平均气温,判断两者是相关关系吗?求回归直线有意义吗?例4观察两相关量得如下数据:求两变量间的回归方程.4、利用回归直线方程对总体进行估计例5炼钢是一个氧化降碳的过程，钢水含碳量的多少直接影响冶炼时间的长短，必须掌握钢水含碳量和冶炼时间的关系。如果已测得炉料熔化完毕时，钢水的含碳量X与冶炼时间y（从炉料熔化完毕到出刚的时间）的一列数据，如下表所示：262626464686866667070物理物理60606565707075758080数学数学EEDDCCBBAA学生学生学科学科62626464686866667070物理物理60606565707075758080数学数学EEDDCCBBAA学生学生学科学科432432701701574574813813507507542542748748年降雨年降雨量量(mm)(mm)13.0513.0512.7412.7413.3313.3313.6913.6912.8412.8412.8412.8412.5112.51年均气年均气温温(c)(c)432432701701574574813813507507542542748748年降雨年降雨量量(mm)(mm)13.0513.0512.7412.7413.3313.3313.6913.6912.8412.8412.8412.8412.5112.51年均气年均气温温(c)(c)9977335511--11--33--55--77--99yy1122443355--55--44--33--22--11xx9977335511--11--33--55--77--99yy1122443355--55--44--33--22--11xx（1）作出散点图，找规律。（2）求回归直线方程。（3）预测当钢水含碳量为160时，应冶炼多少分钟？3125125235235205205170170135135155155185185210210200200100100YY（（minmin））121121204204191191150150134134147147177177190190180180104104xx（（0.01%0.01%））125125235235205205170170135135155155185185210210200200100100YY（（minmin））121121204204191191150150134134147147177177190190180180104104xx（（0.01%0.01%））