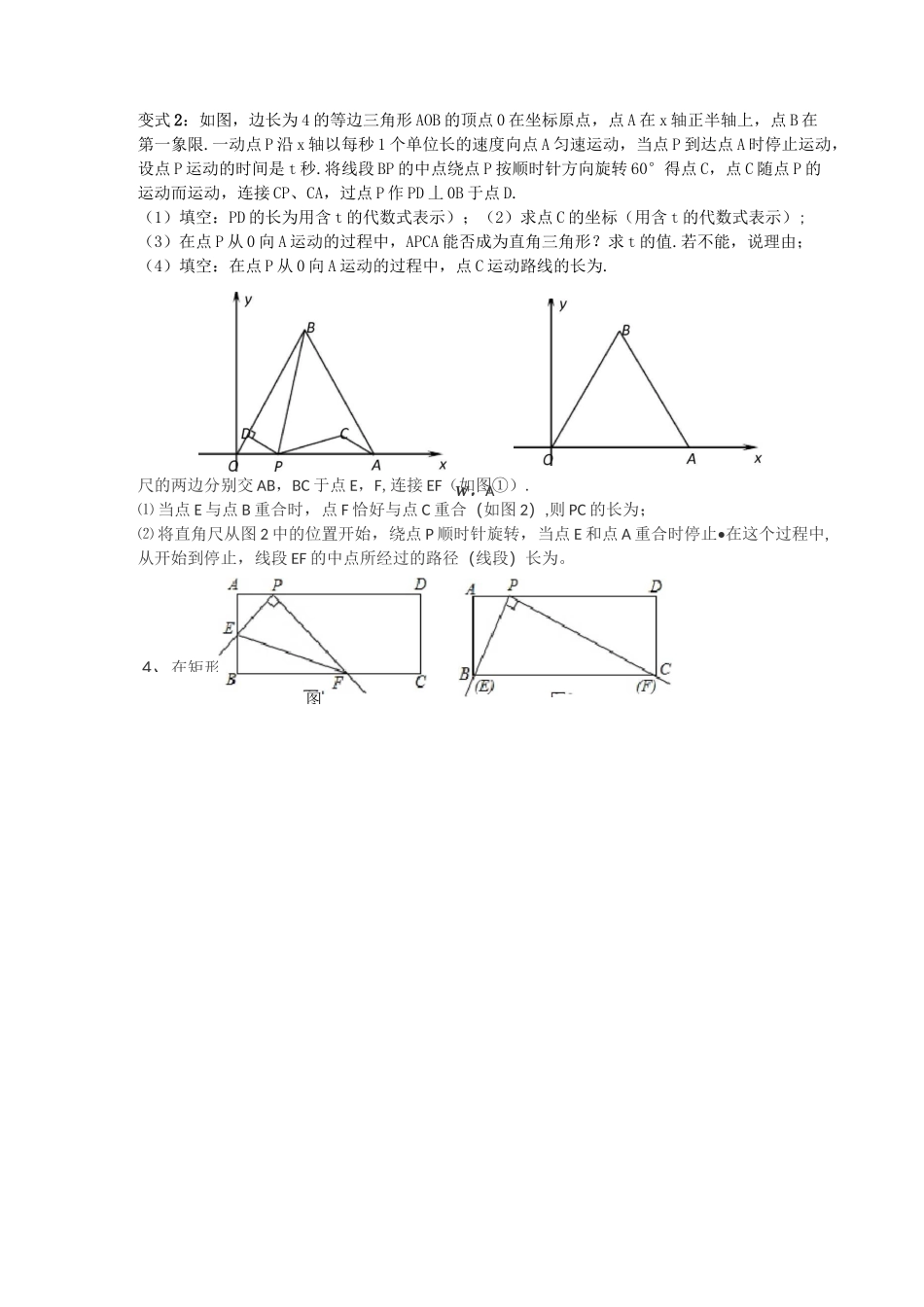
2、如图,已知线段AC=BD=2,点P是CD上一动点,分别以AP、PB为边向上、D时,线段0102中点G的运动路径的长是点的运动轨迹符合一定条件的动点所形成的图形,或者说,符合一定条件的点的全体所组成的集合,叫做满足该条件的点的轨迹."动点路径"是一个比较抽象的问题,但在高中解析几何中的学习是非常有用的,也是非常重要的。在研究动点问题时,可以在运动中寻找不变的量,即不变的数量关系或位置关系.如果动点的轨迹是一条线段,那么其中不变的量便是该动点到某条直线的距离始终保持不变;如果动点的轨迹是一段圆弧,那么其中不变的量便是该动点到某个定点的距离始终保持不变.因此,解决此类动点轨迹问题便可转化为寻找变量与不变的关系。常用的基本轨迹:1、如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边AACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是•变式1、(2010桂林)如图:已知AB=10,点C、D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边AAEP和等边APFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是.变式2、如图:已知AB=10,点C、D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形APEF和正方形PBGH,点0】和O2是这两个正方形的中心,连接0]02,设0]02的中点为Q;当点P从点C运动到点D时,则点Q移动路径的长是.下作正方形APEF和PHKB,设正方形对角线的交点分别为01、02,当点P从点C运动到点曰母题:若x+t=3,y—5二t,则y与x之间的关系是3、如图1,在Rt^ABC中,ZC=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD〃BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t三0).(1)直接用含t的代数式分别表示:QB=,PD=.(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.变式1:如图,在平面直角坐标系中,矩形0ABC的两边0A、0C分别在x轴、y轴的正半轴上,0A=4,0C=2.点P从点0出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.(1)请用含t的代数式表示出点D的坐标;(2)请直接写出随着点P的运动,点D运动路线的长.4、在矩形ABCD中,点P在ADW,A变式2:如图,边长为4的等边三角形AOB的顶点0在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA,过点P作PD丄0B于点D.(1)填空:PD的长为用含t的代数式表示);(2)求点C的坐标(用含t的代数式表示);(3)在点P从0向A运动的过程中,APCA能否成为直角三角形?求t的值.若不能,说理由;(4)填空:在点P从0向A运动的过程中,点C运动路线的长为.尺的两边分别交AB,BC于点E,F,连接EF(如图①).⑴当点E与点B重合时,点F恰好与点C重合(如图2),则PC的长为;⑵将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止•在这个过程中,从开始到停止,线段EF的中点所经过的路径(线段)长为。图变式、如图,直角坐标系中,已知点A(2,4),B(5,0),动点P从B点出发沿BO向终点0运动,动点Q从A点出发沿AB向终点B运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了x秒.(1)Q点的坐标为(,)(用含x的代数式表示);(2)当x为何值时,AAPQ是一个以AP为腰的等腰三角形?(3)记PQ的中点为G.请你直接写出点G随点P,Q运动所经过的路线的长度.5、如图,OA丄OB,垂足为0,P、Q分别是射线OA、OB上的两个动点,点C是线段PQ的中点,且PQ=4.贝y动点C运动形成的路...