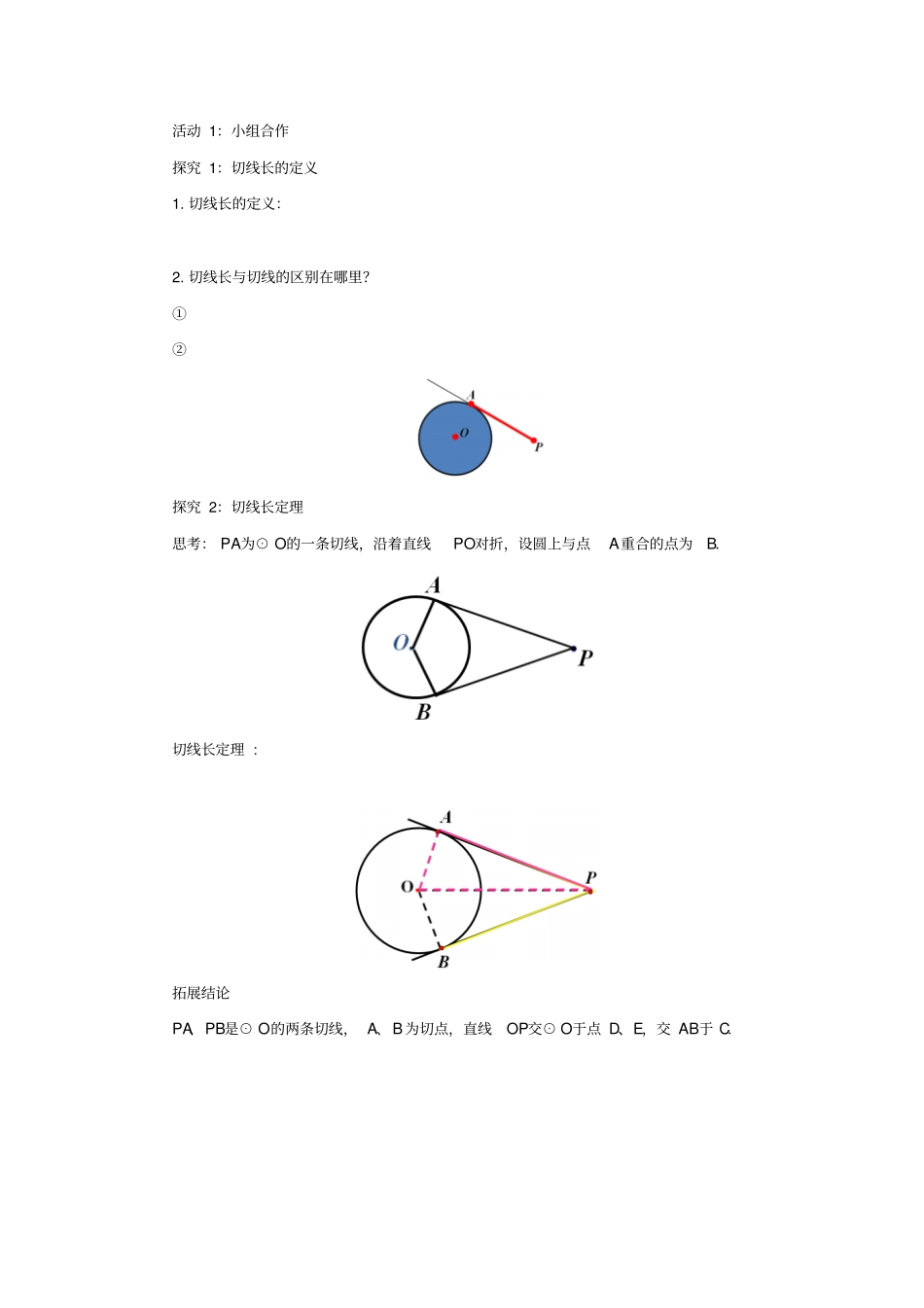
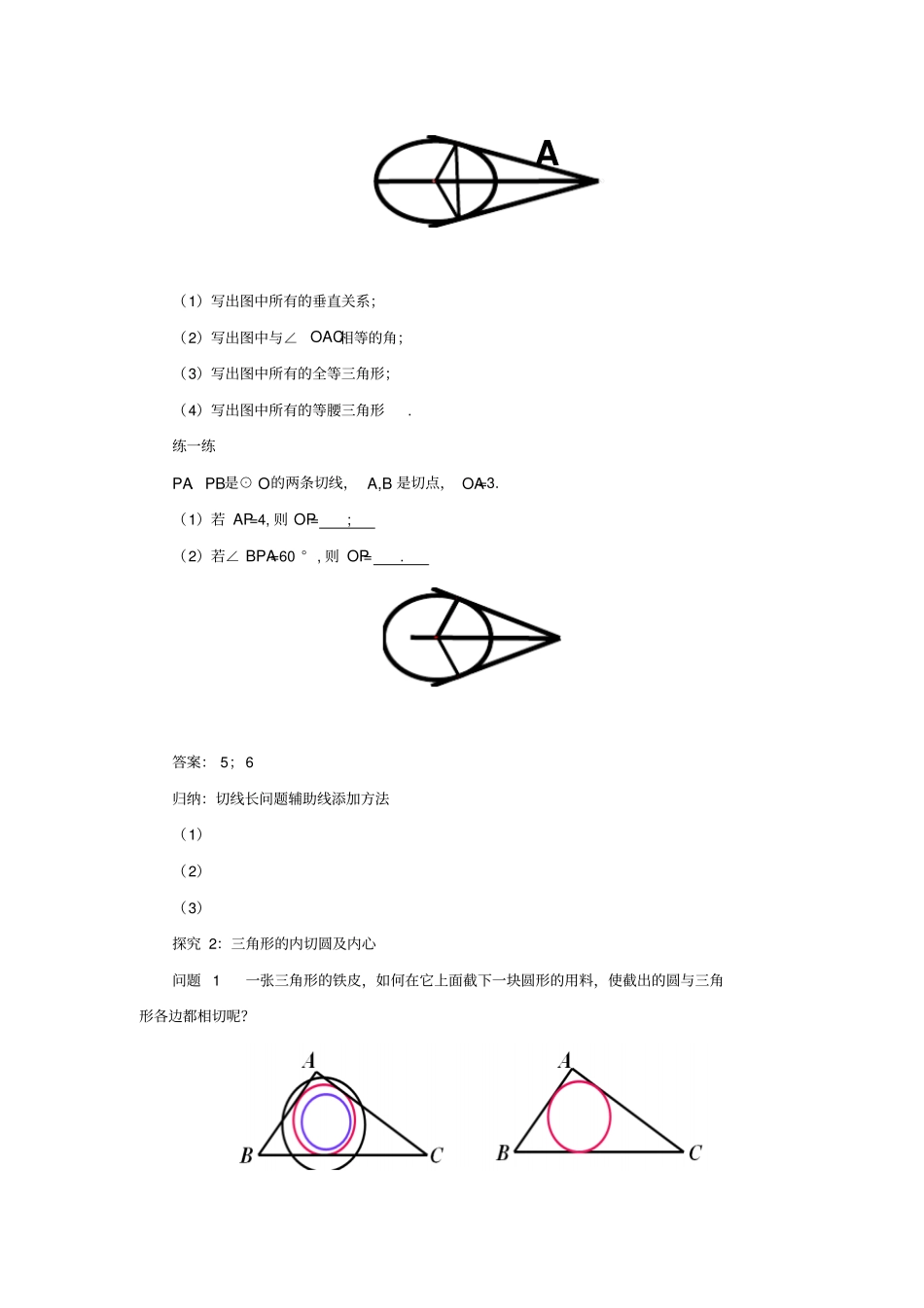
24.2.2直线和圆的位置关系(3)预习案一、预习目标及范围:1.掌握切线长定理,初步学会运用切线长定理进行计算与证明.2.了解有关三角形的内切圆和三角形的内心的概念.3.学会利用方程思想解决几何问题,体验数形结合思想.预习范围:P99-100二、预习要点1、切线长定理:_.2、与三角形各边,叫做三角形的内切圆.3、①当已知三角形的内心时,常常作过三角形的顶点和内心的射线,则这条射线平分三角形的内角.②内心到三角形三边的距离.三、预习检测1、如左下图,PA、PB分别切⊙O于A、B两点,如果∠P=60°,PA=2,那么AB的长为.2、如右下图,正三角形的内切圆半径为1,那么三角形的边长为.探究案一、合作探究活动内容1:活动1:小组合作探究1:切线长的定义1.切线长的定义:2.切线长与切线的区别在哪里?①②探究2:切线长定理思考:PA为⊙O的一条切线,沿着直线PO对折,设圆上与点A重合的点为B.切线长定理:拓展结论PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.(1)写出图中所有的垂直关系;(2)写出图中与∠OAC相等的角;(3)写出图中所有的全等三角形;(4)写出图中所有的等腰三角形.练一练PA、PB是⊙O的两条切线,A,B是切点,OA=3.(1)若AP=4,则OP=;(2)若∠BPA=60°,则OP=.答案:5;6归纳:切线长问题辅助线添加方法(1)(2)(3)探究2:三角形的内切圆及内心问题1一张三角形的铁皮,如何在它上面截下一块圆形的用料,使截出的圆与三角形各边都相切呢?A问题2如何作圆,使它和已知三角形的各边都相切?已知:△ABC.求作:和△ABC的各边都相切的圆.作法:1.2.3.⊙O就是所求的圆.归纳:1.叫做三角形的内切圆2.叫做三角形的内心.3.三角形的内心就是4.三角形的内心到三角形的三边的距离。活动2:探究归纳活动内容2:典例精析例1如图,PA、PB是⊙O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作⊙O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则(1)△PDE的周长是;⑵∠DOE=.例2△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.解:方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.二、随堂检测1.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果AP=4,∠APB=40°,则∠APO=,PB=.2.如图,已知点O是△ABC的内心,且∠ABC=60°,∠ACB=80°,则∠BOC=.3.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P=50°,点C是⊙O上异于A、B的点,则∠ACB=.4.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是.5.直角三角形的两直角边分别是3cm,4cm,试问:(1)它的外接圆半径是cm;内切圆半径是cm?(2)若移动点O的位置,使⊙O保持与△ABC的边AC、BC都相切,求⊙O的半径r的取值范围.参考答案预习检测:1.22.23随堂检测1.20°;42.110°3.65°或115°4.305.解:(1)5,1;(2)如图所示,设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连接OB、OD,则四边形BODC为正方形.∴OB=BC=3,∴半径r的取值范围为0<r≤3.