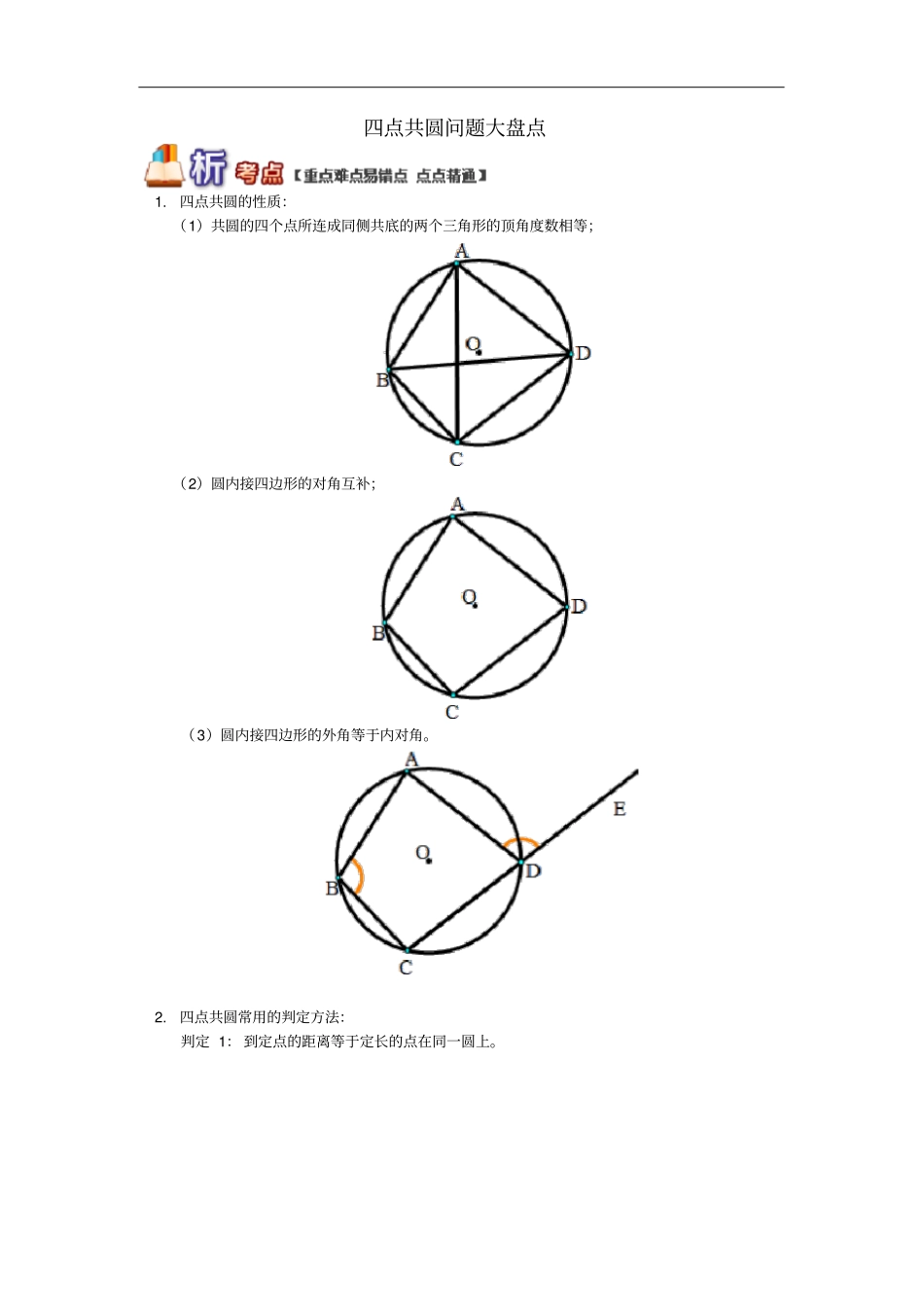
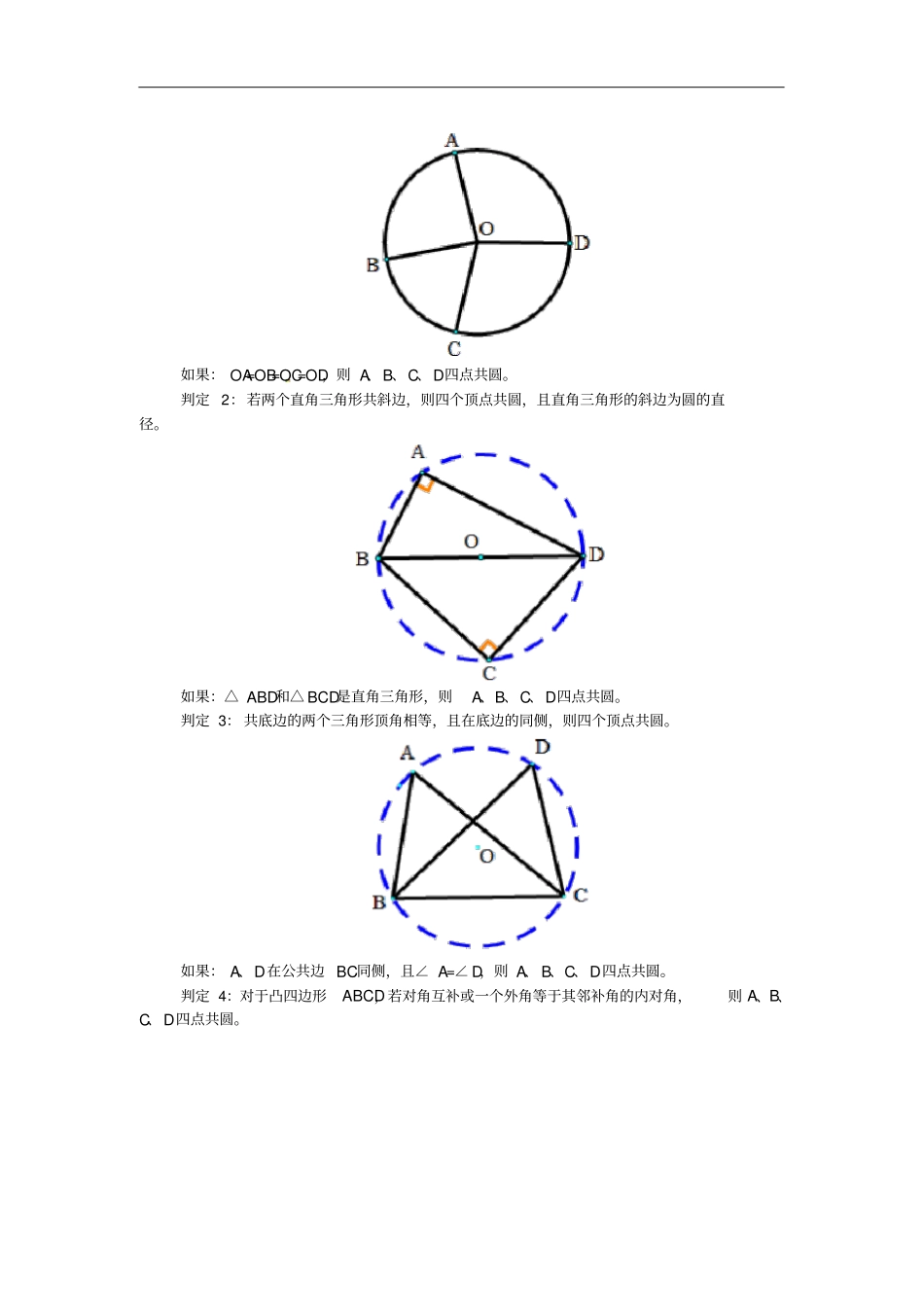
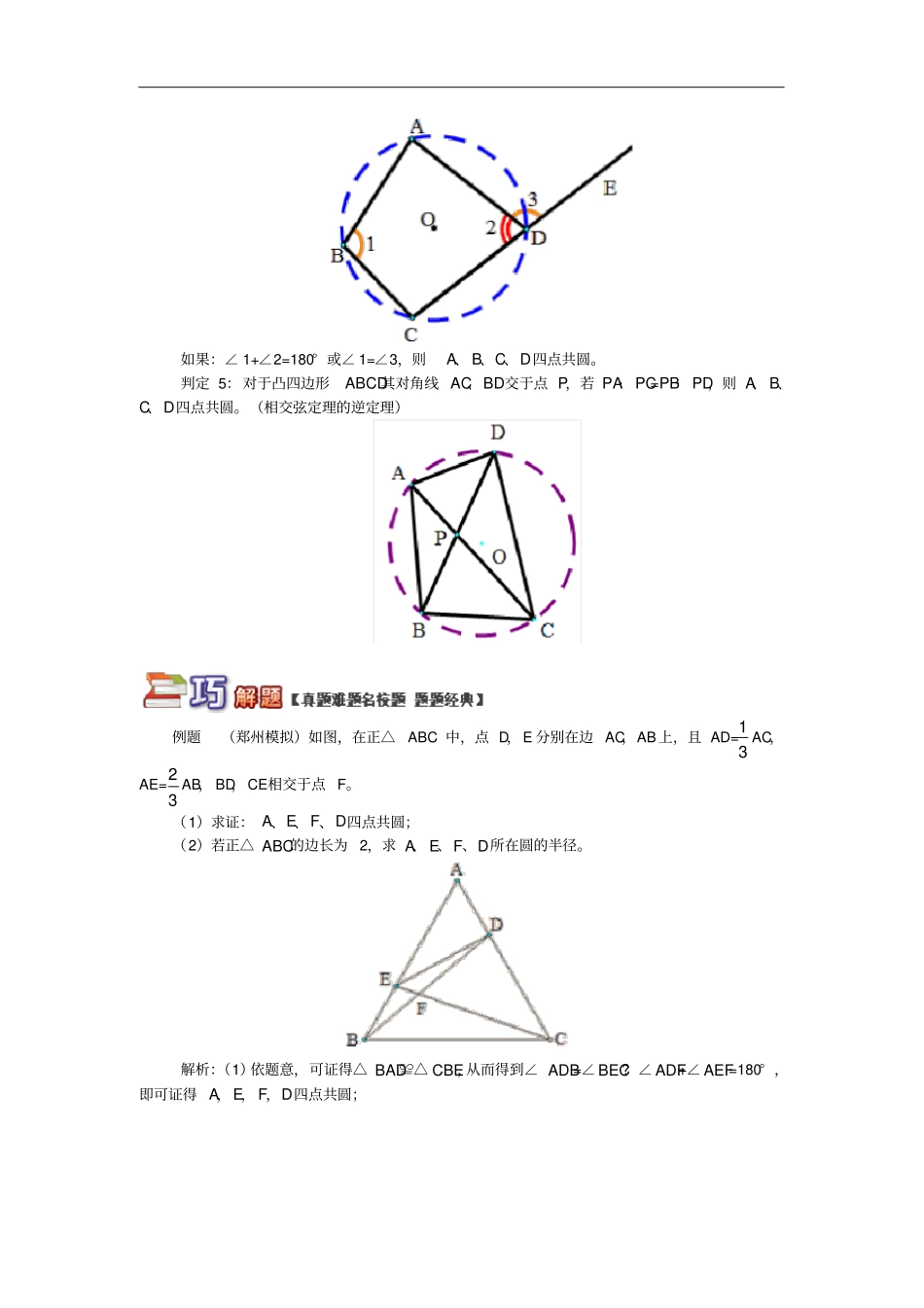
四点共圆问题大盘点1.四点共圆的性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角度数相等;(2)圆内接四边形的对角互补;(3)圆内接四边形的外角等于内对角。2.四点共圆常用的判定方法:判定1:到定点的距离等于定长的点在同一圆上。如果:OA=OB=OC=OD,则A、B、C、D四点共圆。判定2:若两个直角三角形共斜边,则四个顶点共圆,且直角三角形的斜边为圆的直径。如果:△ABD和△BCD是直角三角形,则A、B、C、D四点共圆。判定3:共底边的两个三角形顶角相等,且在底边的同侧,则四个顶点共圆。如果:A、D在公共边BC同侧,且∠A=∠D,则A、B、C、D四点共圆。判定4:对于凸四边形ABCD,若对角互补或一个外角等于其邻补角的内对角,则A、B、C、D四点共圆。如果:∠1+∠2=180°或∠1=∠3,则A、B、C、D四点共圆。判定5:对于凸四边形ABCD其对角线AC、BD交于点P,若PA·PC=PB·PD,则A、B、C、D四点共圆。(相交弦定理的逆定理)例题(郑州模拟)如图,在正△ABC中,点D,E分别在边AC,AB上,且AD=31AC,AE=32AB,BD,CE相交于点F。(1)求证:A、E、F、D四点共圆;(2)若正△ABC的边长为2,求A、E、F、D所在圆的半径。解析:(1)依题意,可证得△BAD≌△CBE,从而得到∠ADB=∠BEC?∠ADF+∠AEF=180°,即可证得A,E,F,D四点共圆;(2)取AE的中点G,连接GD,可证得△AGD为正三角形,GA=GE=GD=32,即点G是△AED外接圆的圆心,且圆G的半径为32。答案:(1)证明: AE=32AB,∴BE=31AB, 在正△ABC中,AD=31AC,∴AD=BE,又 AB=BC,∠BAD=∠CBE,∴△BAD≌△CBE,∴∠ADB=∠BEC,即∠ADF+∠AEF=180°,所以A,E,F,D四点共圆。(2)解:如图,取AE的中点G,连接GD,则AG=GE=12AE, AE=32AB,∴AG=GE=13AB=32, AD=13AC=32,∠DAE=60°,AB=AC∴△AGD为正三角形,∴GD=AG=AD=32,即GA=GE=GD=32,所以点G是△AED外接圆的圆心,且圆G的半径为32,由于A,E,F,D四点共圆,即A,E,F,D四点共圆G,其半径为32。点拨:本题着重考查全等三角形的证明与四点共圆的证明,突出推理能力与分析运算能力的考查,属于难题。【方法定位】将已知条件、欲求的结论以及所给图形的特点三个方面认真分析、思考,即可发现,适当利用四点共圆的有关性质以及定理,就能巧妙地找到解决问题的途径。也就是说,四点共圆有时在解(证)题中起着“搭桥铺路”的作用。例题(河南模拟)如图:AB是⊙O的直径,G是AB延长线上的一点,GCD是⊙O的割线,过点G作AG的垂线,交直线AC于点E,交直线AD于点F,过点G作⊙O的切线,切点为H。(1)求证:C,D,E,F四点共圆;(2)若GH=6,GE=4,求EF的长。解析:(1)连接DB,利用AB是⊙O的直径,可得∠ADB=90°,在Rt△ABD和Rt△AFG中,∠ABD=∠AFE,又同弧所对的圆周角相等可得∠ACD=∠ABD,进而得到∠ACD=∠AFE即可证明四点共圆;(2)由C,D,E,F四点共圆,利用共线定理可得GE·GF=GC·GD。由GH是⊙O的切线,利用切割线定理可得GH2=GC·GD,进而得到GH2=GE·GF。即可答案:证明:(1)连接DB, AB是⊙O的直径,∴∠ADB=90°,在Rt△ABD和Rt△AFG中,∠ABD=∠AFE,又 ∠ABD=∠ACD,∴∠ACD=∠AFE。∴C,D,E,F四点共圆;(2) C,D,E,F四点共圆,∴GE·GF=GC·GD。 GH是⊙O的切线,∴GH2=GC·GD,∴GH2=GE·GF。又因为GH=6,GE=4,所以GF=9。∴EF=GF-GE=9-4=5。点拨:熟练掌握圆的切线的性质、同弧所对的圆周角相等、四点共圆的判定方法、切割线定理等是解题的关键。此题综合性较强,涉及知识点较全面。(答题时间:30分钟)一、选择题1.锐角△ABC的三条高AD、BE、CF交于H,在A、B、C、D、E、F、H七个点中。能组成四点共圆的组数是()A.4组B.5组C.6组D.7组2.如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:①当AC=BD时,M、E、N、F四点共圆。②当AC⊥BD时,M、E、N、F四点共圆。③当AC=BD且AC⊥BD时,M、E、N、F四点共圆。其中正确的是()A.①②B.①③C.②③D.①②③3.如图,A,B,C,D是圆上四点,AD,BC的延长线交于点P,弧AB、弧CD分别为100°、40°,则∠P的度数为()A.40°B.35°C.60°D.30°4...