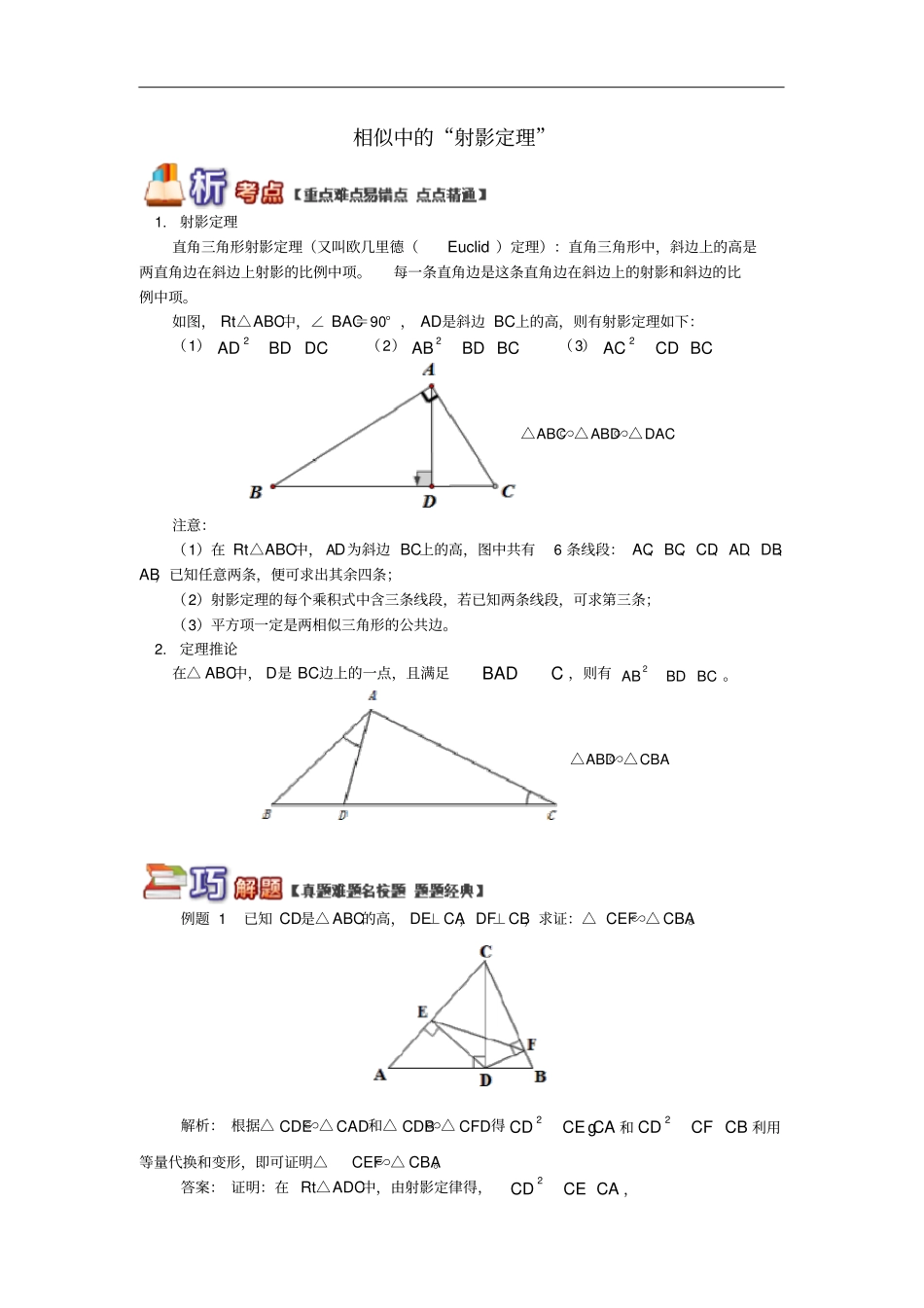
相似中的“射影定理”1.射影定理直角三角形射影定理(又叫欧几里德(Euclid)定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)2ADBDDC(2)2ABBDBC(3)2ACCDBC△ABC∽△ABD∽△DAC注意:(1)在Rt△ABC中,AD为斜边BC上的高,图中共有6条线段:AC、BC、CD、AD、DB、AB,已知任意两条,便可求出其余四条;(2)射影定理的每个乘积式中含三条线段,若已知两条线段,可求第三条;(3)平方项一定是两相似三角形的公共边。2.定理推论在△ABC中,D是BC边上的一点,且满足BADC,则有2ABBDBC。△ABD∽△CBA例题1已知CD是△ABC的高,DE⊥CA,DF⊥CB,求证:△CEF∽△CBA。解析:根据△CDE∽△CAD和△CDB∽△CFD得2CDCECAg和2CDCFCB利用等量代换和变形,即可证明△CEF∽△CBA。答案:证明:在Rt△ADC中,由射影定律得,2CDCECA,在Rt△BCD中,2CDCFCB∴CECACFCB∴CECFCBCA ECFBCA∴△CEF∽△CBA点拨:本题主要考察了相似三角形的基本模型射影定理的应用。做题时要善于发现相似,找出等量关系,进行适当的变形。例题2已知:如图,AB为⊙O的直径,AC为弦,CD⊥AB于D。若AE=AC,BE交⊙O于点F,连接CF、DE。求证:(1)2?AEADAB(2)ACFAED解析:(1)根据AE=AC,可以把结论转化为证明2?ACADAB,只需连接BC,证明△ACD∽△ABC即可。(2)根据(1)中的结论,即可证明三角形ADE相似于三角形AEB,得到∠AED=∠B,再根据同弧所对的圆周角相等即可证明。答案:(1)连接BC, AB为⊙O的直径,∴∠ACB=90° CD⊥AB,∴△ACD∽△ABC,∴ACABADAC AC=AE,∴2?AEADAB(2) 2?AEADAB,∠EAD=∠BAE,∴△ADE∽△AEB,∴∠AED=∠B ∠ACF=∠B,∴∠ACF=∠AED点拨:本题主要考查了对相似三角形的判定和性质的掌握和应用,注意转化思想的应用是解决本题的关键。【要点总结】射影定理是相似三角形中的特殊形式,经常结合圆、矩形、平面直角坐标系和函数考查,因此要善于在复杂的图形中发现满足射影定理的模型,并对其进行代数式的变形,以及等量代换,从而达到解题目的。例题如图,在Rt△ABC中,CD,CE分别是斜边AB上的高和中线,BC=a,AC=b(b>a),若13tanDCE,求ab的值。解析:在Rt△ABC中,利用射影定理得到2?BCBDBA,进而得到BD的表达式,由面积法可求出CD的长,根据CE为中线,建立关系式DE=BE﹣BD,再根据正切函数的定义,建立关于a、b的关系式。答案:在Rt△ABC中, ∠ACB=90°,CD⊥AB∴2?BCBDBA,即:2222BCaBDBAab。由等面积法知:1122abABCD,∴22abCDab。又因为CE是中线,则222222222122abaDEBEBDababab。在Rt△CDE中,13tanDCE,222222123baababab得:223230aabb,解得1103ab,于是有1013ab或1013ab(舍负值)。点拨:本题考查了射影定理、勾股定理、解直角三角形,综合性较强,要认真对待。(答题时间:30分钟)一、选择题1.在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D,若AD:BD=9:4,则AC:BC的值为()A.9:4B.3:2C.4:9D.2:3*2.在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若34ACAB,则BDCD=()A.43B.34C.169D.916*3.已知:在△ABC中,∠BAC=90°,AD⊥BC于D,M为BC中点。下列关系式中正确的是()A.222ACABDMBCB.222ACBCDMACC.222ACABDMACD.222BCABADAC**4.若正实数x,y,z满足①222xyz,②222zxrr。则下列关系式中正确的是()A.xyzrB.xyzrC.xyzrD.无法确定二、填空题*5.如图,△ABC中ABAC,点D在BC上,以8BD为直径作⊙O,恰过A点,若AC与⊙O相切,则AB的长为。*6.如图,矩形ABCD中,56ABBC,点E在BC上,点F在CD上,且16ECBC,35FCCD,FG⊥AE于G,则AG:GE=。*7.两个任意大小的正方形,都可以适当剪开,拼成一个较大的正方形,如用两个边长分别为a,b的正方形拼成一个大正方形。图中Rt△ABC的斜边AB的长等于(用a,b的代数式表示)。*8.Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则222,,ABACAD三者之间的等量关系式为。三、解答题*9.如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D,交AE于点G,弦CE...