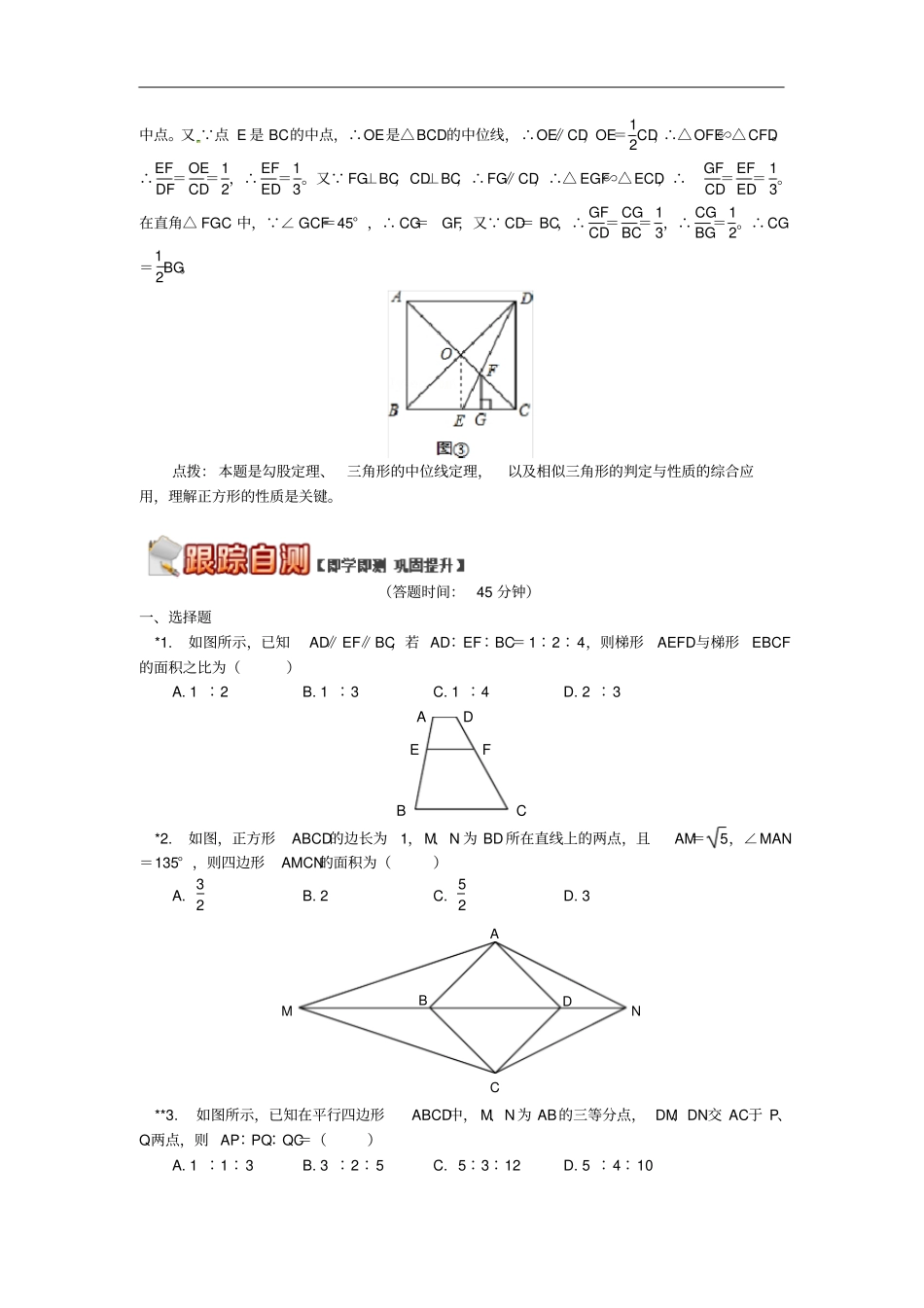
构造相似三角形解题构造相似三角形的基本方法1.由平行得相似,如图①和②;图①图②图③图④2.由同角或等角得相似,如图③;3.由垂直得相似,如图④。方法归纳:在较为复杂的图形中,我们一般通过特殊图形(如等腰三角形、平行四边形、圆等)的边或角构造相似三角形,如需添加辅助线,应考虑添加辅助线后能构成相等的角或比例线段,如:过中点(或等分点)作平行线,过某点作平行或垂直等。总结:1.学会构造相似三角形的方法和技巧,能熟练地将边和角划分到相关的相似三角形中。2.能够综合运用相似三角形的判定和性质解决较为复杂的问题。例题如图所示,四边形ABCD和BEFG均为正方形,则AG∶DF∶CE=()A.1∶1∶1B.1∶2∶1C.1∶2∶3D.1∶2∶1ABCDEFG解析:不难证明△ABG≌△CBE,所以AG=CE。那么,本题只要求AG∶DF即可。要求AG和DF的比需要构造一个含有这两条线段的相似三角形,并且这对相似三角形的相似比要能求出来。在正方形中,边长和对角线的比是可求的,所以本题可试着连接BF和BD,通过三角形相似来求解。答案:连接BF、BD。因为∠ABG=∠ABE-∠EBG=∠ABE-90°,∠CBE=∠ABE-∠ABC=∠ABE-90°。所以∠ABG=∠CBE,又AB=BC,BG=BE,所以△ABG≌△CBE,所以AG=CE。因为∠DBF=∠ABE-∠ABD-∠EBF=∠ABE-45°-45°=∠ABE-90°,所以∠DBF=∠ABG。又因为所有正方形都相似,所以这两个正方形的对角线的比BD∶BF、边长的比AB∶BG,都等于这两个正方形的相似比,即BD∶BF=AB∶BG,所以AB∶BD=BG∶BF,所以△ABG∽△DBF。所以AG∶DF=BG∶BF=1∶2。所以AG∶DF∶CE=1∶2∶1。故选D。ABCDEFG点拨:本题难度大,特别是确定AG和DF的关系是一大难点。解答这类难题,我们束手无策时,一定要展开联想,寻找问题的突破口。如:线段的比往往要通过相似形来求;四边形常常要连接对角线;两个正方形变换形成的三角形中可能有全等三角形;正方形边长和对角线的比是1∶2。利用相似三角形求线段的比例关系时,有些题目根本无法将所求线段构造成相似三角形的对应线段,此类问题通常用如下的方法过渡:再构造一个与之相似的三角形,利用相似三角形的传递性解题;把不能划分到相关相似三角形中的线段进行等量代换等。例题如图,在正方形ABCD中,对角线AC与BD相交于点O,点E是BC上的一个动点,连接DE,交AC于点F。(1)如图①,当CEEB=13时,求S△CEFS△CDF的值;(2)如图②,当DE平分∠CDB时,求证:AF=2OA;(3)如图③,当点E是BC的中点时,过点F作FG⊥BC于点G,求证:CG=12BG。解析:(1)利用相似三角形的性质求得EF与DF的比值,因为△CEF和△CDF同高,所以其面积的比就是EF与DF的比值;(2)利用三角形的外角和定理证得∠ADF=∠AFD,可以证得AD=AF,在直角△AOD中,利用勾股定理可求得AD=2OA,从而得出AF=2OA;(3)连接OE,易证OE是△BCD的中位线,然后根据△FGC是等腰直角三角形,易证△EGF∽△ECD,利用相似三角形的对应边的比相等即可得证。答案:(1)解: CEEB=13,∴CEBC=14。 四边形ABCD是正方形,∴AD∥BC,AD=BC,∴△CEF∽△ADF,∴EFDF=CEAD,∴EFDF=CEBC=14,∴S△CEFS△CDF=EFDF=14。(2)证明: DE平分∠CDB,∴∠ODF=∠CDF,又 AC、BD是正方形ABCD的对角线。∴∠ADO=∠FCD=45°,∠AOD=90°,OA=OD,而∠ADF=∠ADO+∠ODF,∠AFD=∠FCD+∠CDF,∴∠ADF=∠AFD,∴AD=AF,在直角△AOD中,根据勾股定理得:AD=OA2+OD2=2OA,∴AF=2OA。(3)证明:连接OE, 点O是正方形ABCD的对角线AC、BD的交点。∴点O是BD的中点。又 点E是BC的中点,∴OE是△BCD的中位线,∴OE∥CD,OE=12CD,∴△OFE∽△CFD。∴EFDF=OECD=12,∴EFED=13。又 FG⊥BC,CD⊥BC,∴FG∥CD,∴△EGF∽△ECD,∴GFCD=EFED=13。在直角△FGC中, ∠GCF=45°,∴CG=GF,又 CD=BC,∴GFCD=CGBC=13,∴CGBG=12。∴CG=12BG。点拨:本题是勾股定理、三角形的中位线定理,以及相似三角形的判定与性质的综合应用,理解正方形的性质是关键。(答题时间:45分钟)一、选择题*1.如图所示,已知AD∥EF∥BC,若AD∶EF∶BC=1∶2∶4,则梯形AEFD与梯形EBCF...