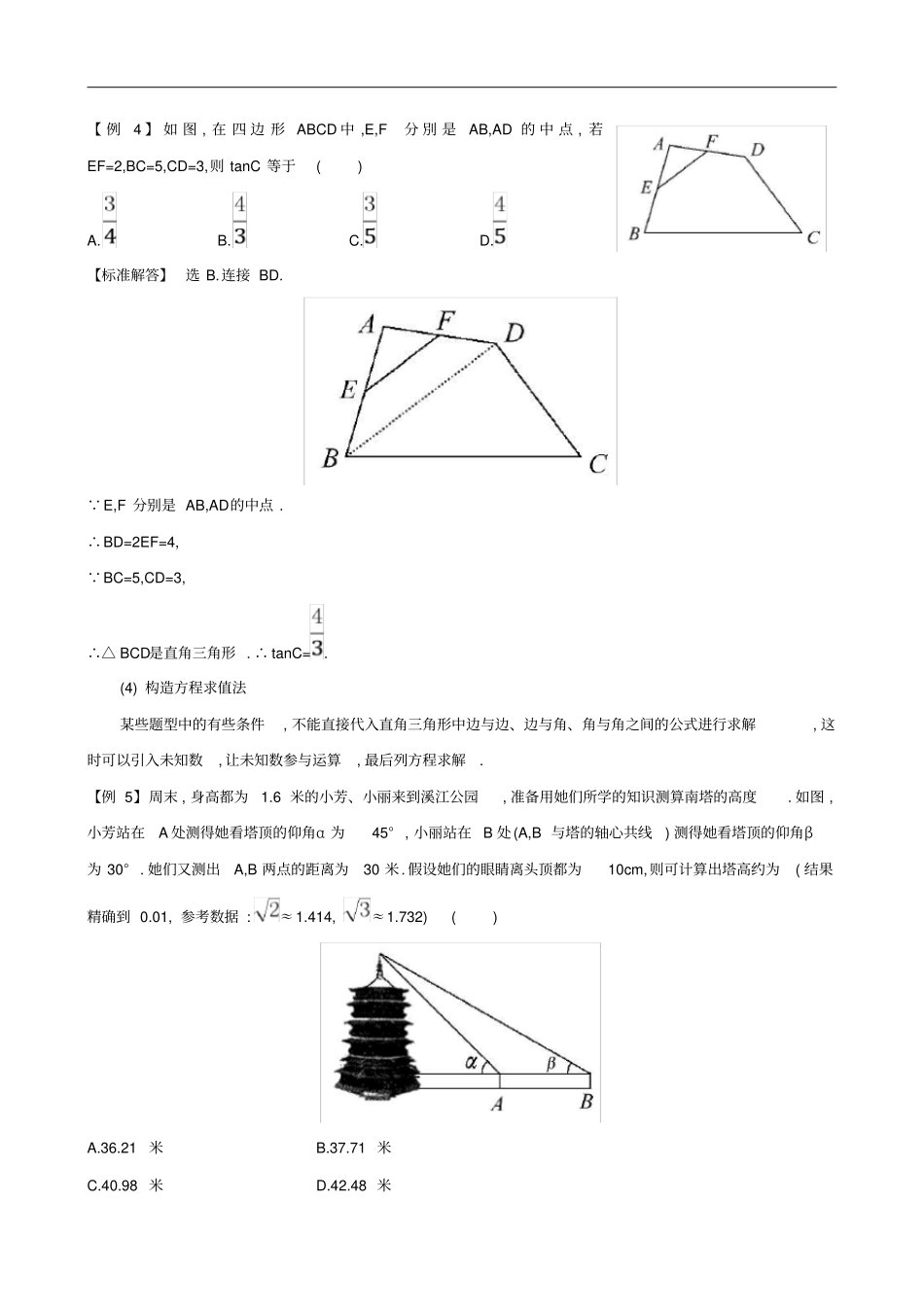
第一章直角三角形的边角关系1.解直角三角形的方法(1)直接利用定义求值法①∠A的正弦sinA==,②∠A的余弦cosA==,③∠A的正切tanA==.概念是解直角三角形的基础,要结合图形记忆理解,它同勾股定理相结合,使得在直角三角形中求边长和锐角度数更加灵活.【例1】在Rt△ABC中,∠C=90°,AC=3,BC=4,则AB=,sinA=.【标准解答】如图, ∠C=90°,AC=3,BC=4,∴AB===5,∴sinA==.答案:5(2)设参数求值法当条件为已知某两条线段比或某一锐角的三角函数值(非特殊角的三角函数值),求图形中其他角的三角函数值时,通常设参数求值,注意参数只是解题的桥梁,不参与最后结果.【例2】在△ABC中,∠C=90°,sinA=,求sinB的值.【标准解答】 sinA=,∴设BC=k,AB=6k.又∠C=90°,故AC==k,∴sinB===.(3)构造直角三角形求值法在某些问题的图形中你根本看不到直角三角形,这时需要你根据条件通过作辅助线构造直角三角形,然后利用直角三角形的相关知识解决问题.当两个直角三角形拥有公共边时,先求出这条公共边是解答此类题的一般思路.【例3】如图,在△ABC中,∠B=45°,cosC=,AC=5a,则△ABC的面积用含a的式子表示是.【标准解答】过点A作AD⊥BC于点D.在Rt△ACD中,AC=5a,cosC=,∴CD=AC·cosC=3a,AD=4a.在Rt△ABD中,AD=4a,∠B=45°,∴BD=AD=4a.∴BC=BD+CD=4a+3a=7a.故=BC·AD=×7a×4a=14a2.答案:14a2【例4】如图,在四边形ABCD中,E,F分別是AB,AD的中点,若EF=2,BC=5,CD=3,则tanC等于()A.B.C.D.【标准解答】选B.连接BD. E,F分别是AB,AD的中点.∴BD=2EF=4, BC=5,CD=3,∴△BCD是直角三角形.∴tanC=.(4)构造方程求值法某些题型中的有些条件,不能直接代入直角三角形中边与边、边与角、角与角之间的公式进行求解,这时可以引入未知数,让未知数参与运算,最后列方程求解.【例5】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A,B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A,B两点的距离为30米.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据:≈1.414,≈1.732)()A.36.21米B.37.71米C.40.98米D.42.48米【标准解答】选D.已知小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A,B与塔的轴心共线)测得她看塔顶的仰角β为30°,A,B两点的距离为30米.假设她们的眼睛离头顶都为10cm,所以设塔高为x米则得=tan30°=,解得:x≈42.48.1.在△ABC中,AB=12,AC=13,cosB=,则BC边长为()A.7B.8C.8或17D.7或172.如图,BD是菱形ABCD的对角线,CE⊥AB于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是()A.B.2C.D.2题图3题图3.如图,已知△ABC的三个顶点均在格点上,则cosA的值为()A.B.C.D.4.如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为.4题图5题图6题图5.如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是.6.如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点.若AC=10,DC=2,则BO=,∠EBD的大小约为度分.(参考数据:tan26°34'≈)7.已知α,β均为锐角,且满足|sinα-|+=0,则α+β=.8.如图,在?ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E.(1)求证:AC⊥BD.(2)若AB=14,cos∠CAB=,求线段OE的长.9.如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.(1)求BD·cos∠HBD的值.(2)若∠CBD=∠A,求AB的长.10.如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:(1)BC的长.(2)sin∠ADC的值.2.解直角三角形的实际应用(1)俯角、仰角问题利用解直角三角形知识解决实际问题的关键是把实际问题转化为数学问题,并构造直角三角形.解题时要认真审题,读懂题意,弄清仰角、俯角的含义,然后再作图解答.【例1】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1m)【标准解答】设CE=xm,则由题意可知BE=xm,AE=(x+100)m.在Rt△AEC中,tan∠CAE=,即tan30°=,∴=,3x=(x+100),解得...