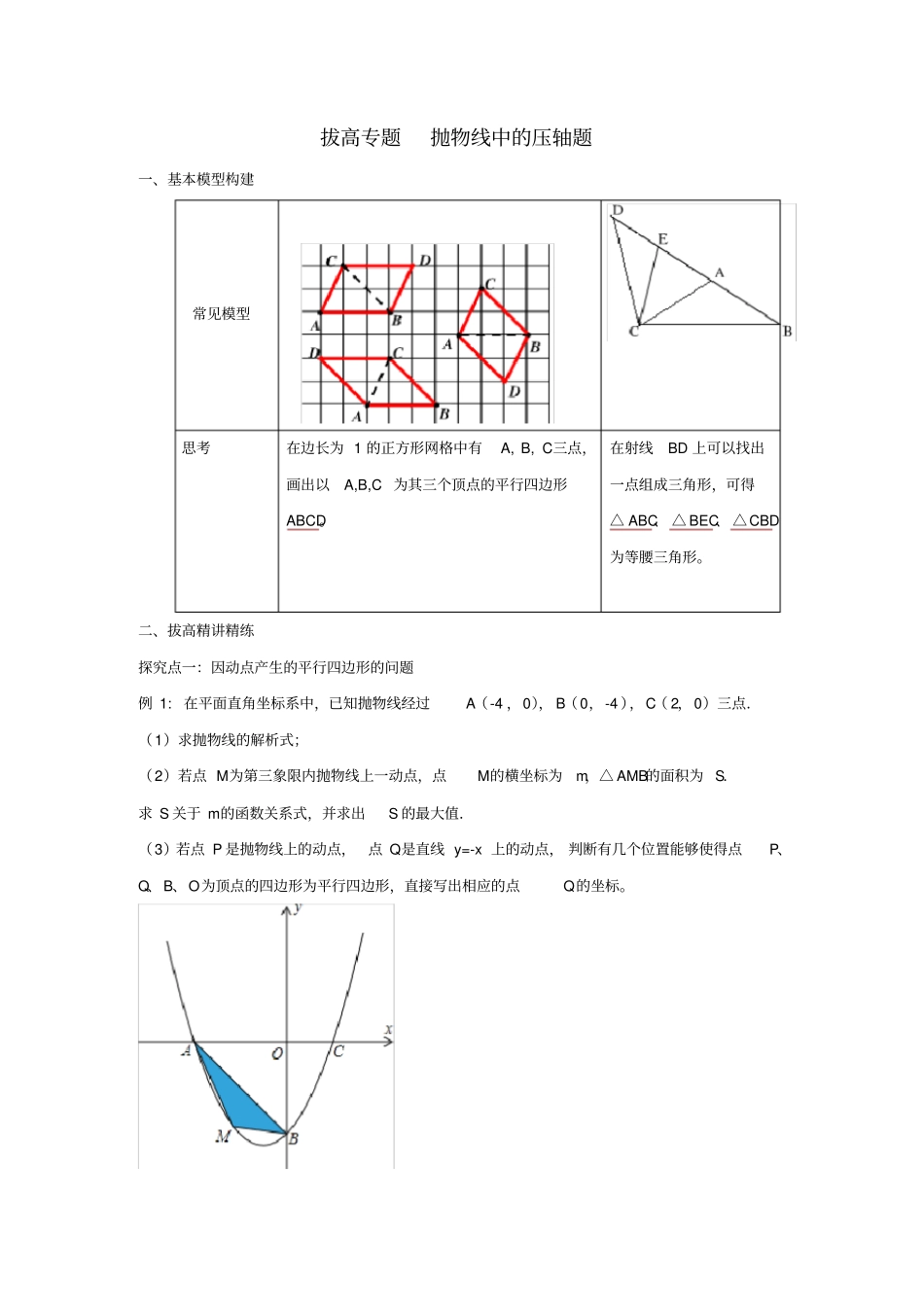
拔高专题抛物线中的压轴题一、基本模型构建常见模型思考在边长为1的正方形网格中有A,B,C三点,画出以A,B,C为其三个顶点的平行四边形ABCD。在射线BD上可以找出一点组成三角形,可得△ABC、△BEC、△CBD为等腰三角形。二、拔高精讲精练探究点一:因动点产生的平行四边形的问题例1:在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标。解:(1)设此抛物线的函数解析式为:y=ax2+bx+c(a≠0),将A(-4,0),B(0,-4),C(2,0)三点代入函数解析式得:16404420abccabc===解得1412abc===,所以此函数解析式为:y=12x2+x-4;(2) M点的横坐标为m,且点M在这条抛物线上,∴M点的坐标为:(m,12m2+m-4),∴S=S△AOM+S△OBM-S△AOB=12×4×(-12m2-m+4)+12×4×(-m)-12×4×4=-m2-2m+8-2m-8=-m2-4m=-(m+2)2+4, -4<m<0,当m=-2时,S有最大值为:S=-4+8=4.答:m=-2时S有最大值S=4.(3)设P(x,12x2+x-4).当OB为边时,根据平行四边形的性质知PQ∥OB,且PQ=OB,∴Q的横坐标等于P的横坐标,又 直线的解析式为y=-x,则Q(x,-x).由PQ=OB,得|-x-(12x2+x-4)|=4,解得x=0,-4,-2±25.x=0不合题意,舍去.如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=-x得出Q为(4,-4).由此可得Q(-4,4)或(-2+25,2-25)或(-2-25,2+25)或(4,-4).【变式训练】(2015?贵阳)如图,经过点C(0,-4)的抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-2,0),B两点.(1)a>0,b2-4ac>0(填“>”或“<”);(2)若该抛物线关于直线x=2对称,求抛物线的函数表达式;(3)在(2)的条件下,连接AC,E是抛物线上一动点,过点E作AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点E的坐标;若不存在,请说明理由.解:(1)a>0,b2-4ac>0;(2) 直线x=2是对称轴,A(-2,0),∴B(6,0), 点C(0,-4),将A,B,C的坐标分别代入y=ax2+bx+c,解得:a=13,b=-43,c=-4,∴抛物线的函数表达式为y=13x2-43x-4;(3)存在,理由为:(i)假设存在点E使得以A,C,E,F为顶点所组成的四边形是平行四边形,过点C作CE∥x轴,交抛物线于点E,过点E作EF∥AC,交x轴于点F,如图1所示,则四边形ACEF即为满足条件的平行四边形, 抛物线y=13x2-43x-4关于直线x=2对称,∴由抛物线的对称性可知,E点的横坐标为4,又 OC=4,∴E的纵坐标为-4,∴存在点E(4,-4);(ii)假设在抛物线上还存在点E′,使得以A,C,F′,E′为顶点所组成的四边形是平行四边形,过点E′作E′F′∥AC交x轴于点F′,则四边形ACF′E′即为满足条件的平行四边形,∴AC=E′F′,AC∥E′F′,如图2,过点E′作E′G⊥x轴于点G, AC∥E′F′,∴∠CAO=∠E′F′G,又 ∠COA=∠E′GF′=90°,AC=E′F′,∴△CAO≌△E′F′G,∴E′G=CO=4,∴点E′的纵坐标是4,∴4=13x2-43x-4,解得:x1=2+27,x2=2-27,∴点E′的坐标为(2+27,4),同理可得点E″的坐标为(2-27,4)。【教师总结】因动点产生的平行四边形问题,在中考题中比较常见,考生一般都能解答,但是解题时需要考虑各种可能性,以免因答案不全面.主要有以下几种类型:(1)已知三个定点,再找一个顶点构成平行四边形;(2)已知两个顶点,再找两个顶点构成平行四边形。①确定两定点的线段为一边,则两动点连接的线段和已知边平行且相等;②两定点连接的线段没确定为平行四边形的边时,则这条线段可能为平行四边形的边或对角线。探究点二:因动点产生的等腰三角形的问题例2:(2015?铜仁市)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(...