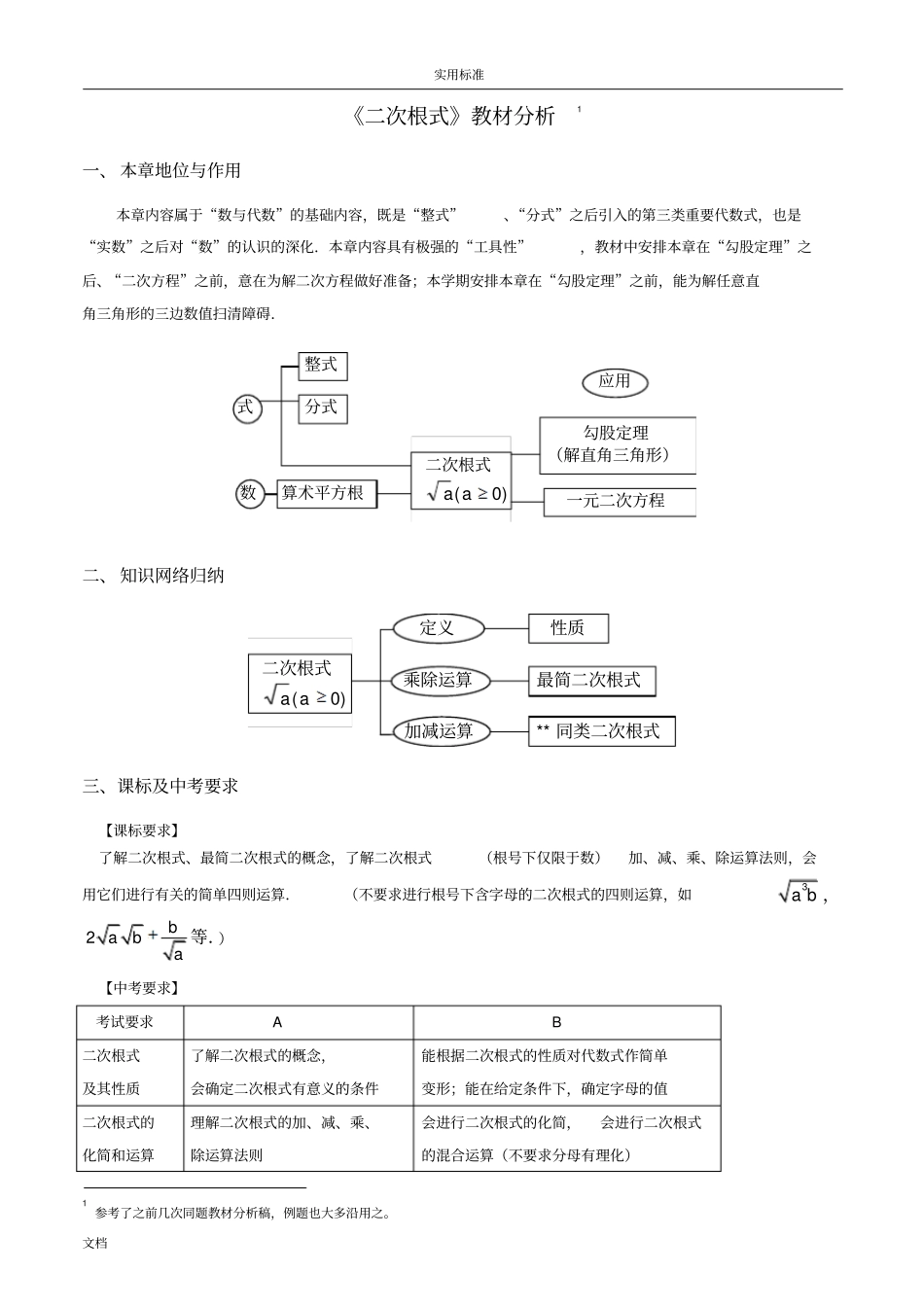
实用标准文档《二次根式》教材分析1一、本章地位与作用本章内容属于“数与代数”的基础内容,既是“整式”、“分式”之后引入的第三类重要代数式,也是“实数”之后对“数”的认识的深化.本章内容具有极强的“工具性”,教材中安排本章在“勾股定理”之后、“二次方程”之前,意在为解二次方程做好准备;本学期安排本章在“勾股定理”之前,能为解任意直角三角形的三边数值扫清障碍.整式数式算术平方根勾股定理(解直角三角形)一元二次方程分式二次根式)0(aa应用二、知识网络归纳性质最简二次根式二次根式)0(aa定义乘除运算加减运算**同类二次根式三、课标及中考要求【课标要求】了解二次根式、最简二次根式的概念,了解二次根式(根号下仅限于数)加、减、乘、除运算法则,会用它们进行有关的简单四则运算.(不要求进行根号下含字母的二次根式的四则运算,如3ab,2baba等.)【中考要求】考试要求AB二次根式及其性质了解二次根式的概念,会确定二次根式有意义的条件能根据二次根式的性质对代数式作简单变形;能在给定条件下,确定字母的值二次根式的化简和运算理解二次根式的加、减、乘、除运算法则会进行二次根式的化简,会进行二次根式的混合运算(不要求分母有理化)1参考了之前几次同题教材分析稿,例题也大多沿用之。实用标准文档四、课时安排建议21.1二次根式约2课时21.2二次根式的乘除约2课时21.3二次根式的加减约3~4课时数学活动与小结约2课时五、全章教学建议1.注意本章内容的“工具性”.二次根式相关知识的学习是为后续勾股定理、二次方程的学习打基础,因此应重点落实二次根式的性质、化简和计算(特别是实数的化简和计算)的准确性,提高学生的计算能力.尽管课本中的例题相对简单,但不要忽视它们在学生建立知识结构的过程所起的过渡作用.非实验班不建议在此补充涉及代数式化简、运算技巧的内容(如分母有理化等),相应地,学探诊测试6第6题及之后的题目可不作为基本教学要求.2.从提出二次根式的概念开始,就注意强化“二次根式在一定条件下才有意义”这一观念.避免教材第7页小贴士“在本章中,如果没有特别说明,所有的字母都表示正数”给学生带来的误解和误导.总有为数不少的学生将二次根式有意义的“非负性”条件误记为“正性”条件,可能与此有关.3.注意对“实数”一章知识的复习,体现“数式通性”的原则;注意与“整式”、“分式”相关知识的联系,相关结论可以类比记忆.4.注意教材和学探诊中,有些题目需要用到勾股定理,可先回避.六、各小节教学建议21.1二次根式(1)实例引入,注意复习开平方、算术平方根的概念和符号表示.(2)二次根式的形式定义:建议不要把精力放在辨别一个式子是否为二次根式上,而应该侧重于理解被开方数是非负数(不要误记为正数)的要求.例如,2是二次根式吗?按本人的理解,2作为单独一个数应属于单项式,非二次根式.学探诊92页第6题:下列各式中,一定是二次根式的是:(A)23(B)2(0.3)(C)2(D)x,答案B.本人认为题干应该改为“下列各二次根式一定有意义的是”.总之,真正该提醒学生的是“数式通性”:如果被开方数是一个常数,那么它不可以是负数;如果被开方数含字母,那么它有取值范围的限制(与分式类似).(3)二次根式(根号)的双重非负性:)0(,0aa;(4)教材要求掌握的公式:2()(0)aaa,2(0)aaa,实用标准文档建议授课时提高要求,理解并掌握)0()0(2aaaaaa.2a与2)(a的对比:①运算顺序不同:2)(a是先求算术平方根再平方,2a是先平方再求算术平方根;②a的取值不同:2)(a中a的取值是0a,而2a中a的取值是任意实数;③运算结果不同:2)(a=a(0a);2a=)0()0(||aaaaa.(5)代数式的概念:建议适当补充一些代数式的书写规范(如果之前没有讲过).例1:当x是怎样的实数时,下列各式在实数范围内有意义?(1)1x;(2)1x;(3)11x;(4)11x.答案:(1)1x;(2)1x;(3)1x;(4)0x且1x.实用标准文档提高题:求下列函数解析式中自变量x的取值范围:(1)2yx-x23;(2)yx-11x;(3)21||2xyx;(4)222yxx.答案:(1)322x;(2)0x且1x;(3)12x且2x;(4)全体实数.例2:若...