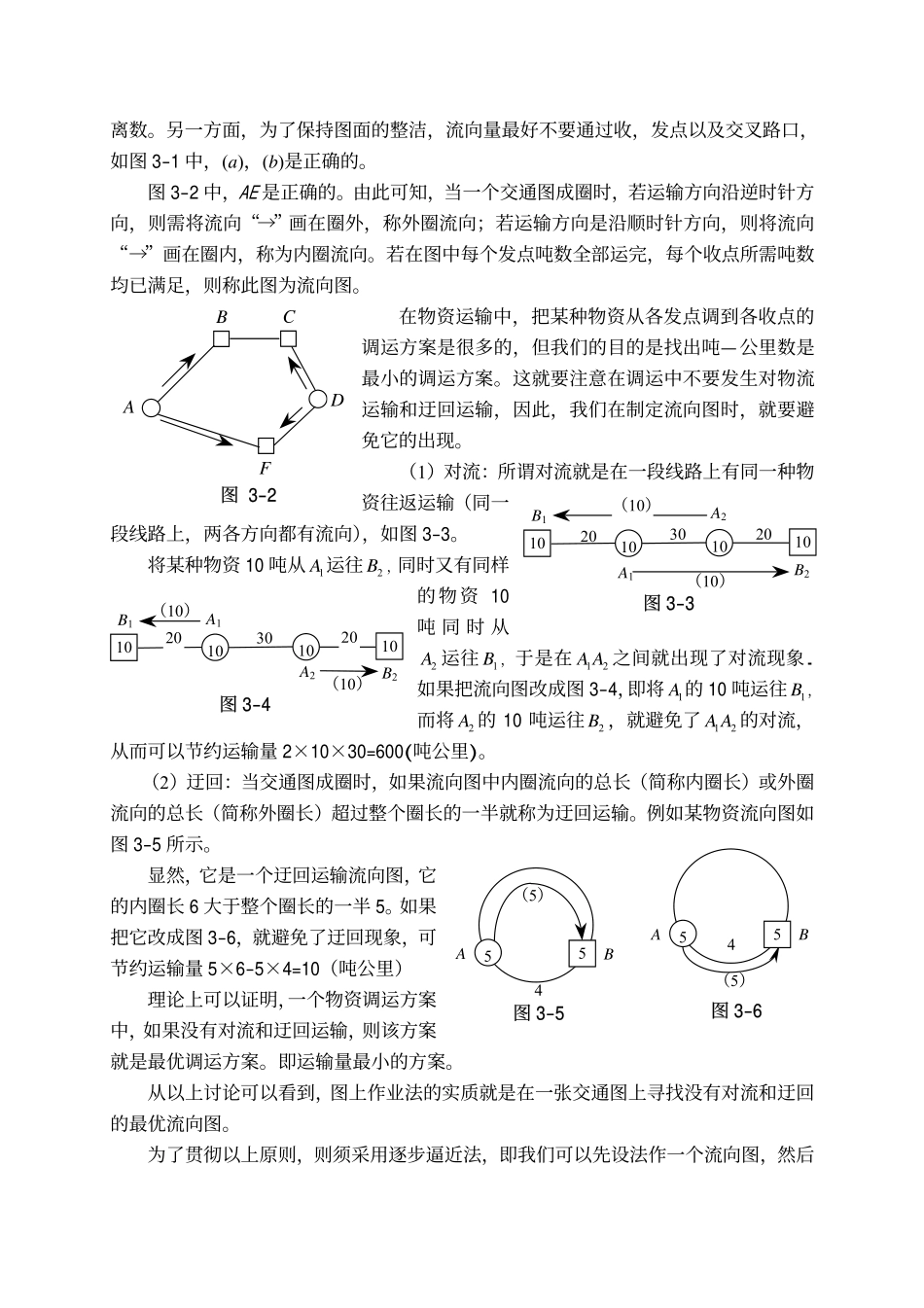
第3章运输问题的求解方法物资最佳调运问题是属于线性规划的一种特殊类型——运输问题。它的解法很多,在这一章里将介绍两种求解方法-----------表上作业法和图上作业法。3.1平衡运输问题及数模3.1.1问题的提出社会生产活动川流不息、工农之间、地区之间、各生产企业之间、各企业车间之间,必然产生不间断的,错综复杂的经济联系。这种联系是由交通运输业的货物运输来实现的。无论地区范围内的运输或者工地范围内的运输,在组织运输时,必须选择合理的物资调运方案。选择合理的物资调运方案是运输工作组织中十分重要的问题,特别是当物资的需要特点(收点)及供应地点(发点)较多,而需要的供应数量又各不相同时,如何根据具体条件,各个收发点的分布,交通运输线路的位置及其他条件等,科学地确定最为合理,经济的调运方案,对于充分发挥运输工具的潜力,降低运输成本,保证建设任务的完成有着极为重要的作用。3.1.2平衡运输问题的数模设为出发点,(1,2,,iAim=⋯))(1,2,,jBjn=⋯为收点,a和b分别表示和ijiAjB的发量和收量,和ijCijx分别表示到iAjB的单位运费和运量。则有线性规划模型。1111min()(1,2,,)(1,2,,)0(1,2,,;1,2,,)mnijijijnijijmijjiijfxcxstxaimxbjnximj=====⋅====≥==∑∑∑∑����njb在这里假定11ij,且,c。满足以上条件的运输问题被称为平衡运输模型,为了叙述方便起见,采用(T,P)表示。mnia===∑∑,0ijab≥0ij≥3.1.3(T,P)的特性1.(T,P)的系数矩阵A的秩为1mn++。因为,A的前行相加的结果等于后行相加的结果,所以,它的行的行向量是线性相关的,秩不可能超过mnmn+1mn++。另一方面,我们还可以在A中找到一个m+n-1阶的非奇异方阵,从而可知A的秩只能为1mn++。并由此可推知,(T,P)的每个基本可行解的基变量的个数为个。1+mn+2.任一个(T,P)问题至少有一个最优解存在。(1)(T,P)至少有如下的一个可行解:(1,2,,;1,2,,)ijijabximjQ===��nb其中,。11mnijijQa====∑∑(2)它的目标函数显然有下界零(非负)。故由(1),(2)知(T,P)必有最优解存在。3.2图上作业法图上作业法是解决(T,P)问题的一个方法,它是在一张运输交通上通过一定步骤的规划和计算来完成物资调运计划的编制工作,以便使物资运行的总吨-----------公里数最小可使物资运费降低,并缩短了运输时间,所以,在一定条件下称这样的方案为最优方案。制定一个物资调运方案时,首先要编制物资平衡表(如表3-1)。在编制物资平衡表时需要做3件事。1.出需要调出物资的地点(即发点)及发量。2.出需要调进物资的地点(即收点)及收量。3.求:总发量=总收量。第二步,根据物资平衡表和收点,发点间的相互位置绘制交通图。所谓交通图就是表明收点和发点间的相互位置以及联结这些点之间的交通线路的简要地图。在交通图上,用圆圈“〇”表示发点,将该发点的发量填入圆圈“〇”内。用方框“□”表示收点,将该收点的收量填入方框“□”内。两点间的距离,记在交通线路的旁边。交通图绘制好后,即可在其上面进行物资调运,找出初始调运方案(初始基可行解)。即第三步,作物资调运流向图。我们用箭头“→”表示物资调运的方向即称流向,并规定:流向“→”必须画在沿着线路前进的右侧。把运送物资的数量记在流向“→”的旁边并加括号(),以区别于两点之间的距B(c)AAB(b)B(a)A图3-1离数。另一方面,为了保持图面的整洁,流向量最好不要通过收,发点以及交叉路口,如图3-1中,(a),(b)是正确的。图3-2中,AE是正确的。由此可知,当一个交通图成圈时,若运输方向沿逆时针方向,则需将流向“→”画在圈外,称外圈流向;若运输方向是沿顺时针方向,则将流向“→”画在圈内,称为内圈流向。若在图中每个发点吨数全部运完,每个收点所需吨数均已满足,则称此图为流向图。在物资运输中,把某种物资从各发点调到各收点的调运方案是很多的,但我们的目的是找出吨—公里数是最小的调运方案。这就要注意在调运中不要发生对物流运输和迂回运输,因此,我们在制定流向图时,就要避免它的出现。(1)对流:所谓对流就是在一段线路上有同一种物资往返运输(同一段线路上,两各方向都...