振动与波动习题VIP免费

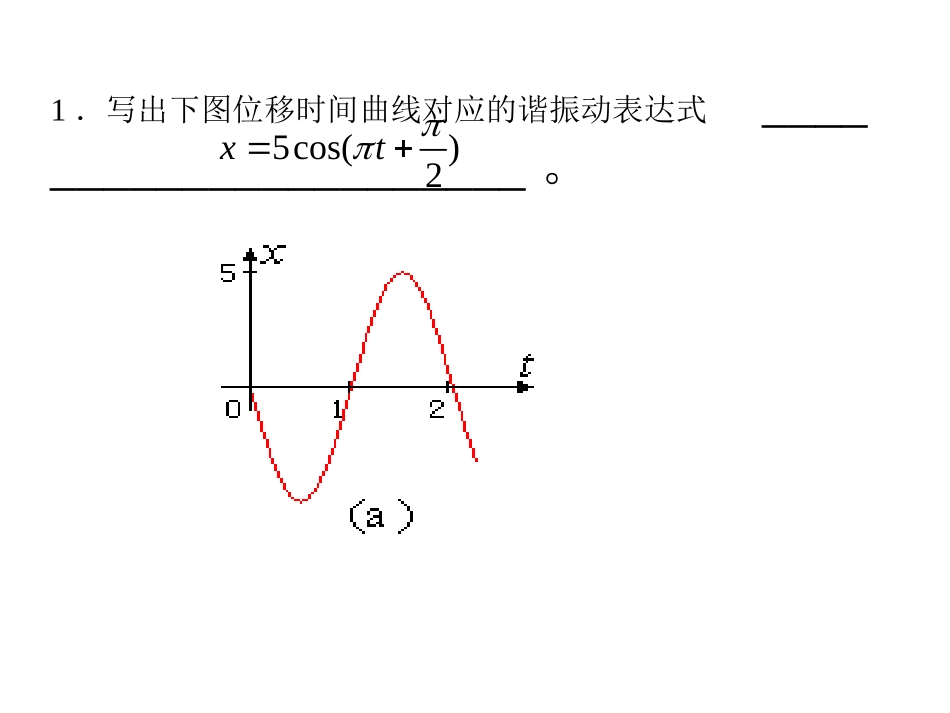
振动与波动习题1．写出下图位移时间曲线对应的谐振动表达式______________________。5cos()2xt2.做简谐振动的小球。速度的最大值为vm=3cm/s,振幅为A=2cm,若速度为正最大值时为计时零点，则小球振动的周期为；加速度的最大值为；振动表达式为。4/324.5/cms30.02cos()22xtcos()sin()xAtAt32423T2cos()aAtmaxmax4.5/acms)4/3cos(tAyA(D)AAoytoytA(A)oytoyt(B)(C)AA3.已知一质点沿ｙ轴作简谐振动．其振动方程为与之对应的振动曲线是4.一质点作简谐振动，周期为T．当它由平衡位置向x轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A)T/12.(B)T/8．(C)T/6．(D)T/4一质点沿x轴做简谐振动，振动方程为，从t=0时刻起，到质点位置在x=-2cm处，且向x轴正方向运动的最短时间间隔为多少？（要求画出旋转矢量图，表示出两个时刻的旋转矢量）。0.52ts2410cos(2/3)xt33x0已知一质点沿y轴做简谐振动，平衡位置在y轴的原点处。振幅A=3cm,角频率=。在下列三种计时零点的选择下，写出该简谐振动的方程。(1)选择质点经平衡位置且向y轴负方向运动时为计时零点；（2）选择质点经y=-3cm时为计时零点；(3)选择质点经y=1.5cm且向y轴正方向运动时为计时零点。（要求用旋转矢量法求初相）0.03cos()2yt0.03cos()yt0.03cos()3yt0y25.质量为2kg的质点，按方程沿着x轴振动．求：(1)t=0时，作用于质点的力的大小；(2)作用于质点的力的最大值和此时质点的位置．)]6/(5sin[2.0tx2/5.2)]6/(5sin[5smtaNmaF56.有一单摆，摆长为l=100cm，开始观察时(t=0)，摆球正好过x0=-6cm处，并以v0=20cm/s的速度沿x轴正向运动，若单摆运动近似看成简谐振动．试求(1)振动频率；(2)振幅和初相.glg2020)(xA1.一弹簧振子，弹簧的倔强系数为k=25N/m.初始动能为0.2J，初始势能为0.6J.则其振幅为；位移x=时，动能与势能相等；位移是振幅的一半时，势能是。0.08100.25m0.0851.78m0.2J210.20.60.82kAJ1.625A22111222kxkA2Ax221112242AkkA2.质量为m的物体在x轴上以平衡位置为坐标原点做谐振动，振幅为A，频率为v，若取x=A/2处为弹性势能的零点，则在x=A处的弹性势能Ep＝；若t=0时刻物体在x=A处由静止释放，则它到达x=-A/2处所需的最短时间是。22232mvA13vkm2v224kmv2221132228pAEkAkkA0x62263t3.一质点做简谐振动，已知振动频率为f，则振动动能的变化频率是。2f2221sin()2kEmAt221[1cos2()]2mAt4.有两个谐振动：，，且有A2