工程力学例题VIP免费

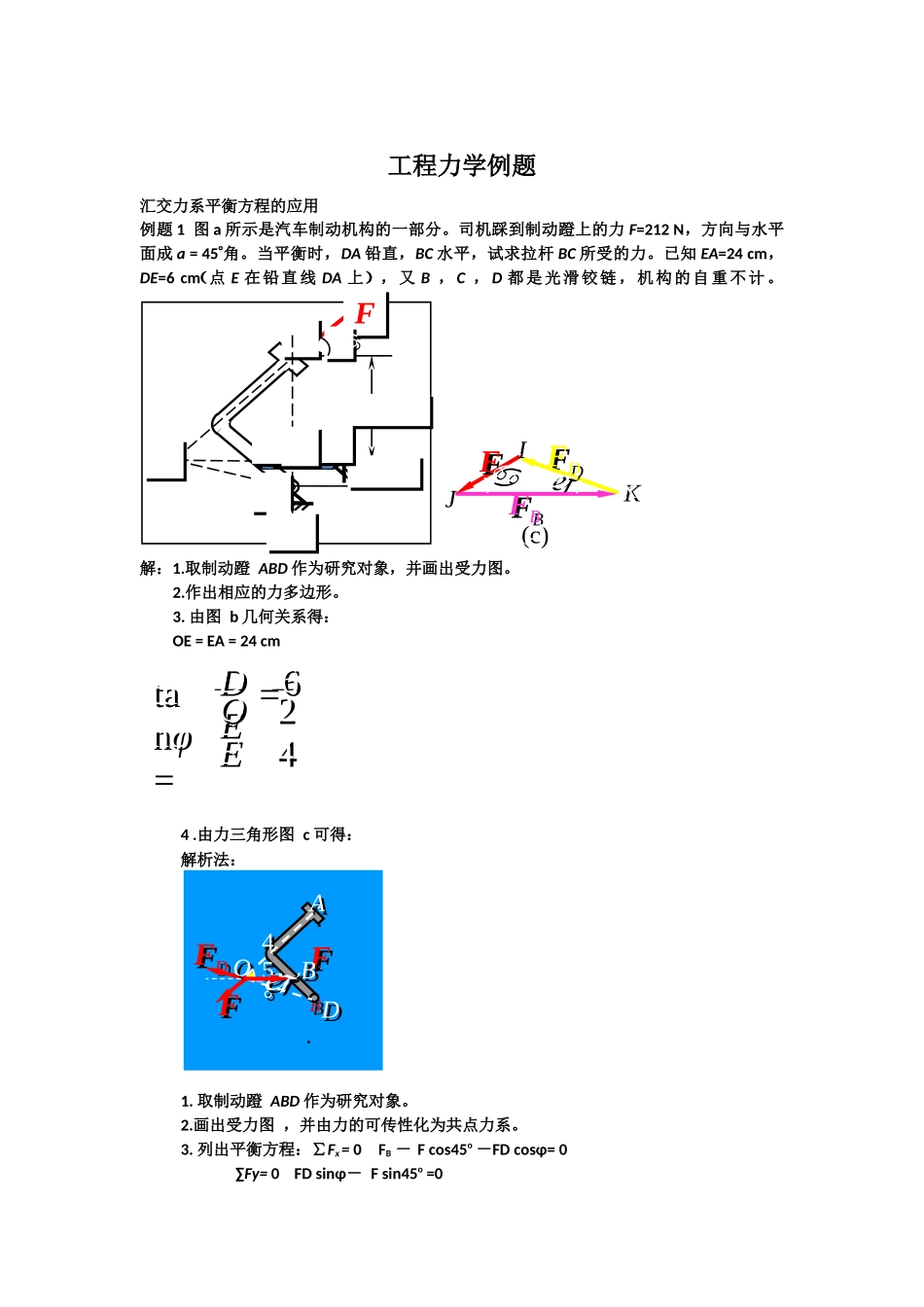
工程力学例题汇交力系平衡方程的应用例题1图a所示是汽车制动机构的一部分。司机踩到制动蹬上的力F=212N，方向与水平面成a=45°角。当平衡时，DA铅直，BC水平，试求拉杆BC所受的力。已知EA=24cm，DE=6cm(点E在铅直线DA上)，又B，C，D都是光滑铰链，机构的自重不计。解：1.取制动蹬ABD作为研究对象，并画出受力图。2.作出相应的力多边形。3.由图b几何关系得：OE=EA=24cm4.由力三角形图c可得：解析法：1.取制动蹬ABD作为研究对象。2.画出受力图，并由力的可传性化为共点力系。3.列出平衡方程：∑Fx=0FB－Fcos45o－FDcosφ=0∑Fy=0FDsinφ－Fsin45o=0FF24cm24cm6cm6cmAACCBBDDOO(a)(a)EEJJFDFDKKFBFBFFII(c)(c)tanφ=tanφ=DEDEOEOE662424==FFFDFDFBFBAABBDDOO45°45°已知：φ=14.01o,sinφ=0.243,cosφ=0.969联立求解得FB=750N例题2水平梁AB中点C作用着力F，其大小等于2kN，方向与梁的轴线成60º角，支承情况如图a所示，试求固定铰链支座A和活动铰链支座B的约束力。梁的自重不计。解：1.取梁AB作为研究对象。2.画出受力图。3.作出相应的力多边形。4.由力多边形解出：FA=Fcos30°=17.3kNFB=Fsin30°=10kN例题3支架的横梁AB与斜杆DC彼此以铰链C连接，并各以铰链A，D连接于铅直墙上，如图所示。已知杆AC=CB；杆DC与水平线成45o角；载荷F=10kN，作用于B处。设梁和杆的重量忽略不计，求铰链A的约束力和杆DC所受的力。A60ºFFB30ºaaCAºB30ºaaC(a)FBFBFAFAD60º30º(b)EFFFBFBFAFA60º30ºH(c)FFADCB45ABCEFF45FCFCFAFA解：取AB为研究对象，其受力如图为，按比例画力F，作出封闭力三角形。量取FA、FC得：FA=22.4kNFC=28.3kN例题4利用铰车绕过定滑轮B的绳子吊起一货物重G=20kN，滑轮由两端铰接的水平刚杆AB和斜刚杆BC支持于点B。不计铰车的自重，试求杆AB和BC所受的力。解：1.取滑轮B轴销作为研究对象。2.画出受力图。3.列出平衡方程：∑Fx=0FBCcos30o+FAB－Fsin30o=0∑Fy=0FBCcos60o－G－Fcos30o=0联立求解得FAB=－54.5kNFBC=74.5kN例题5如图所示，重物G=20kN，用钢丝绳挂在支架的滑轮B上，钢丝绳的另一端绕在铰车D上。杆AB与BC铰接，并以铰链A，C与墙连接。如两杆与滑轮的自重不计并忽略摩擦和滑轮的大小，试求平衡时杆AB和BC所受的力。ABD3060CG解：取滑轮B为研究对象，忽略滑轮的大小，画受力图。FT=G列平衡方程：∑Fx=0－FAB－FTcos30o+FTcos60o=0∑Fy=0FBC－FTcos30o－FTcos60o=045FFabd30°30°BBGGAACC30°30°aayyFBCFBCFFFABFABGGxx30°30°30°30°bbBBFABFABFTFTFTFTFBCFBC解方程得:FAB=-0.366G=-7.312KNFBC=1.366G=27.32KN例题6梯长AB=l，重G=100N，重心假设在中点C，梯子的上端A靠在光滑的端上，下端B放置在与水平面成40°角的光滑斜坡上，求梯子在自身重力作用下平衡时，两端的约束力以及梯子和水平面的夹角θ。解：梯子受三力平衡，由三力汇交定理可知,它们交于D点。1.求约束力。列平衡方程：∑Fx=0FA－FBcos(φ+θ)=0∑Fy=0－G+FBsin(φ+θ)=0考虑到j+q=90°-40°=50°，联立求解，得：FA=83.9NFB=130.5N2.求角θ。角θ可由三力汇交的几何关系求出。由直角三角形BEC和BED，有:EC=EBtanθED=EBtan(φ+θ)EC=0.5EDtanθ=0.5tan(φ+θ)=0.5tan50o=0.596θ=30.8o例题7车间用的悬臂式简易起重机可简化为如图所示的结构。AB是吊车梁，BC是钢索，A端支承可简化为铰链支座。设已知电葫芦和提升重物G=5kN,θ=25o，AD=a=2m,AB=l=2.5m。如吊车梁的自重可略去不计，求钢索BC和铰A的约束力。把三个力移到点O，作直角坐标系，如图b所示。列平衡方程：∑Fx=0FAcosφ－FBcosθ=040°40°θθAACCBBGGyyxxFAFAFBFBGGAACCEEBBDD40°40°AABBCCDDθθGGAABBDDGGOOaallφφθθFAFAFBFByyOOxxGGFAFAFBFBφφθθ（b）（b）∑Fy=0－G+FAsinφ+FBsinθ=0式中角φ可由图b中的几何关系求得tanφ=0.117FA=8.63kNFB=9.46kN例题8如图所示，用起重机吊起重物。起重杆的A端用球铰链固定在地面上，而B端则用绳CB和DB拉住，两绳分别系在墙上的C点和D点，连线CD平行于x轴。已知CE=EB=DE,角α=30o，CDB平面与水平面间的夹角∠EBF=30o,重物G=10k...