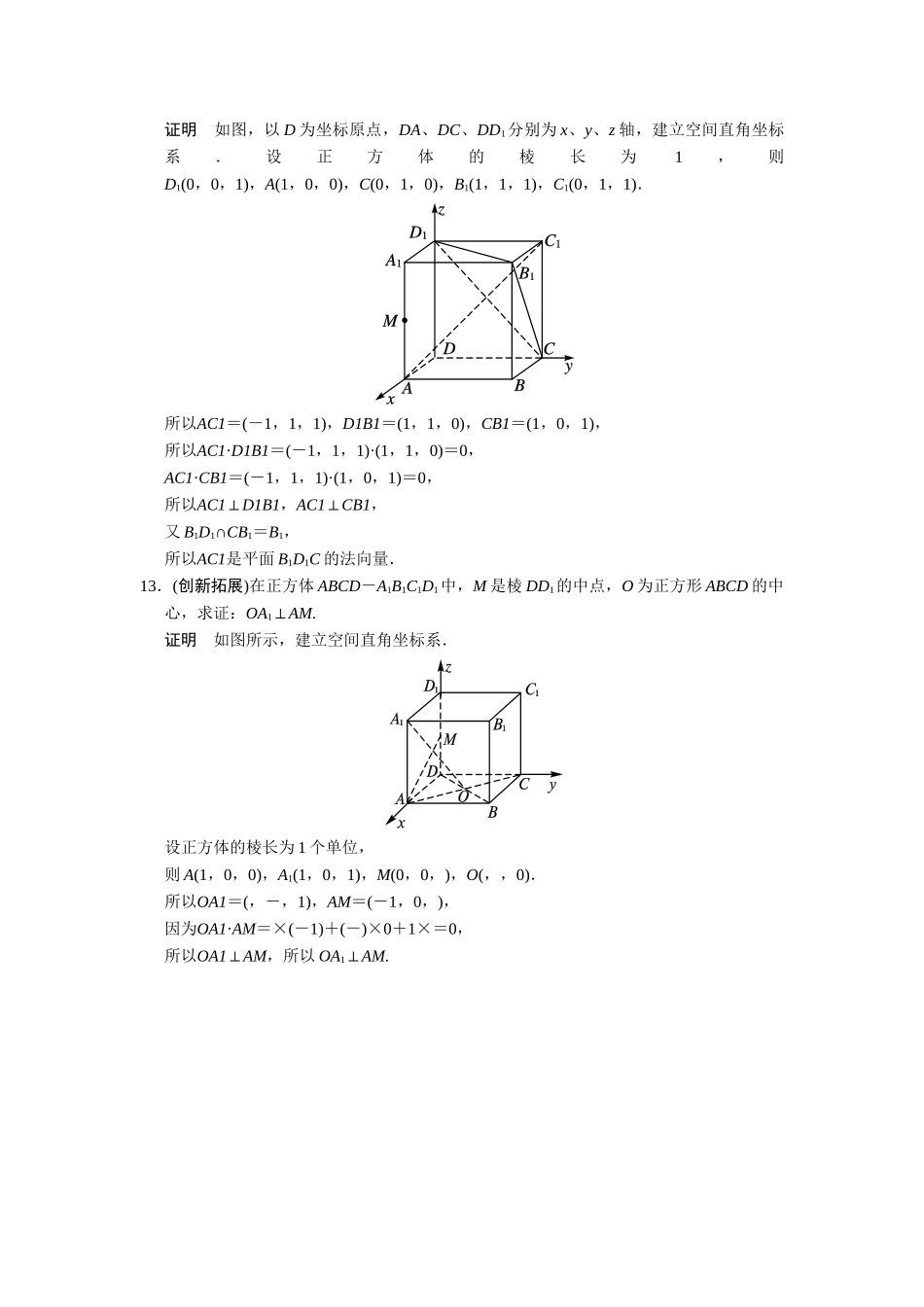
3.2空间向量的应用3.2.1直线的方向向量与平面的法向量双基达标限时20分钟1.在空间直角坐标系O-xyz中,下列向量中不是y轴方向向量的序号是________.①(0,1,0);②(0,-1,0);③(0,2,0);④(0,1,1).解析y轴方向向量可以表示为(0,k,0)(k≠0),所以只有④(0,1,1)不是y轴方向向量.答案④2.设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k),若α∥β,则k=________.解析α∥β⇒(-2,-4,k)=λ(1,2,-2),∴λ=-2,k=4.答案43.在空间直角坐标系O-xyz中,平面xOy的一个法向量是________.解析答案不唯一,只要与向量(0,0,1)平行的非零向量都可以.答案(0,0,1)4.在空间直角坐标系O-xyz中,法向量(1,0,0)对应的坐标平面是________.解析因为向量(1,0,0)平行于x轴,所以对应的坐标平面是垂直于x轴的平面.答案yOz平面5.在空间直角坐标系O-xyz中,设平面α经过点P(1,0,0),平面α的法向量为e=(1,0,0),M(x,y,z)为平面α内任意一点,则x,y,z满足的关系是________.解析由题意可知e·PM=0,代入坐标计算即可得x=1.答案x=16.已知平面α经过三点A(1,2,3),B(2,0,-1),C(3,-2,0),试求平面α的一个法向量.解∵A(1,2,3),B(2,0,-1),C(3,-2,0),∴AB=(1,-2,-4),AC=(2,-4,-3),设平面α的法向量为n=(x,y,z).依题意,应有n·AB=0,n·AC=0.即,解得.令y=1,则x=2.∴平面α的一个法向量为n=(2,1,0).综合提高(限时25分钟)7.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的单位法向量坐标为________.解析设单位法向量n0=(x,y,z),AB=(-1,1,0),AC=(-1,0,1).由n0·AB=0,且n0·AC=0得解得或答案(,,)或(-,-,-)8.已知点A、B、C的坐标分别是(0,1,0)、(-1,0,1)、(2,1,1),点P的坐标为(x,0,z),若PA⊥AB,PA⊥AC,则点P的坐标为________.解析∵A(0,1,0),B(-1,0,1),C(2,1,1),P(x,0,z),∴AB=(-1,-1,1),AC=(2,0,1),PA=(-x,1,-z).∴PA⊥AB,PA⊥AC,∴PA·AB=(-x,1,-z)·(-1,-1,1)=0,PA·AC=(-x,1,-z)·(2,0,1)=0,∴∴∴点P的坐标为(,0,-).答案(,0,-)9.若不重合的两个平面的法向量分别是a=(3,-3,-3),b=(-1,1,1),则这两个平面的位置关系是________.解析因为a=-3b,所以a∥b,所以这两个平面平行.答案平行10.不重合的直线l1,l2的方向向量分别为a,b,且a=(2,3,-1),b=(-6,-9,3),则l1,l2的位置关系是________.解析因为a=-3b,所以a∥b,所以l1∥l2.答案平行11.△ABC中,A(1,-1,2),B(3,3,1),C(3,1,3),设M(x,y,z)是平面ABC上任一点.(1)求平面ABC的一个法向量;(2)求x,y,z满足的关系式.解(1)设平面ABC的法向量n=(a,b,c),∵AB=(2,4,-1),AC=(2,2,1),∴,∴.故可取n=(-3,2,2).∴平面ABC的一个法向量为n=(-3,2,2).(2)∵点M(x,y,z)是平面ABC上任一点,∴-3(x-1)+2(y+1)+2(z-2)=0.3∴x-2y-2z-1=0.这就是所求的x、y、z满足的关系式.12.在正方体ABCD-A1B1C1D1中,求证:AC1是平面B1D1C的法向量.证明如图,以D为坐标原点,DA、DC、DD1分别为x、y、z轴,建立空间直角坐标系.设正方体的棱长为1,则D1(0,0,1),A(1,0,0),C(0,1,0),B1(1,1,1),C1(0,1,1).所以AC1=(-1,1,1),D1B1=(1,1,0),CB1=(1,0,1),所以AC1·D1B1=(-1,1,1)·(1,1,0)=0,AC1·CB1=(-1,1,1)·(1,0,1)=0,所以AC1⊥D1B1,AC1⊥CB1,又B1D1∩CB1=B1,所以AC1是平面B1D1C的法向量.13.(创新拓展)在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O为正方形ABCD的中心,求证:OA1⊥AM.证明如图所示,建立空间直角坐标系.设正方体的棱长为1个单位,则A(1,0,0),A1(1,0,1),M(0,0,),O(,,0).所以OA1=(,-,1),AM=(-1,0,),因为OA1·AM=×(-1)+(-)×0+1×=0,所以OA1⊥AM,所以OA1⊥AM.