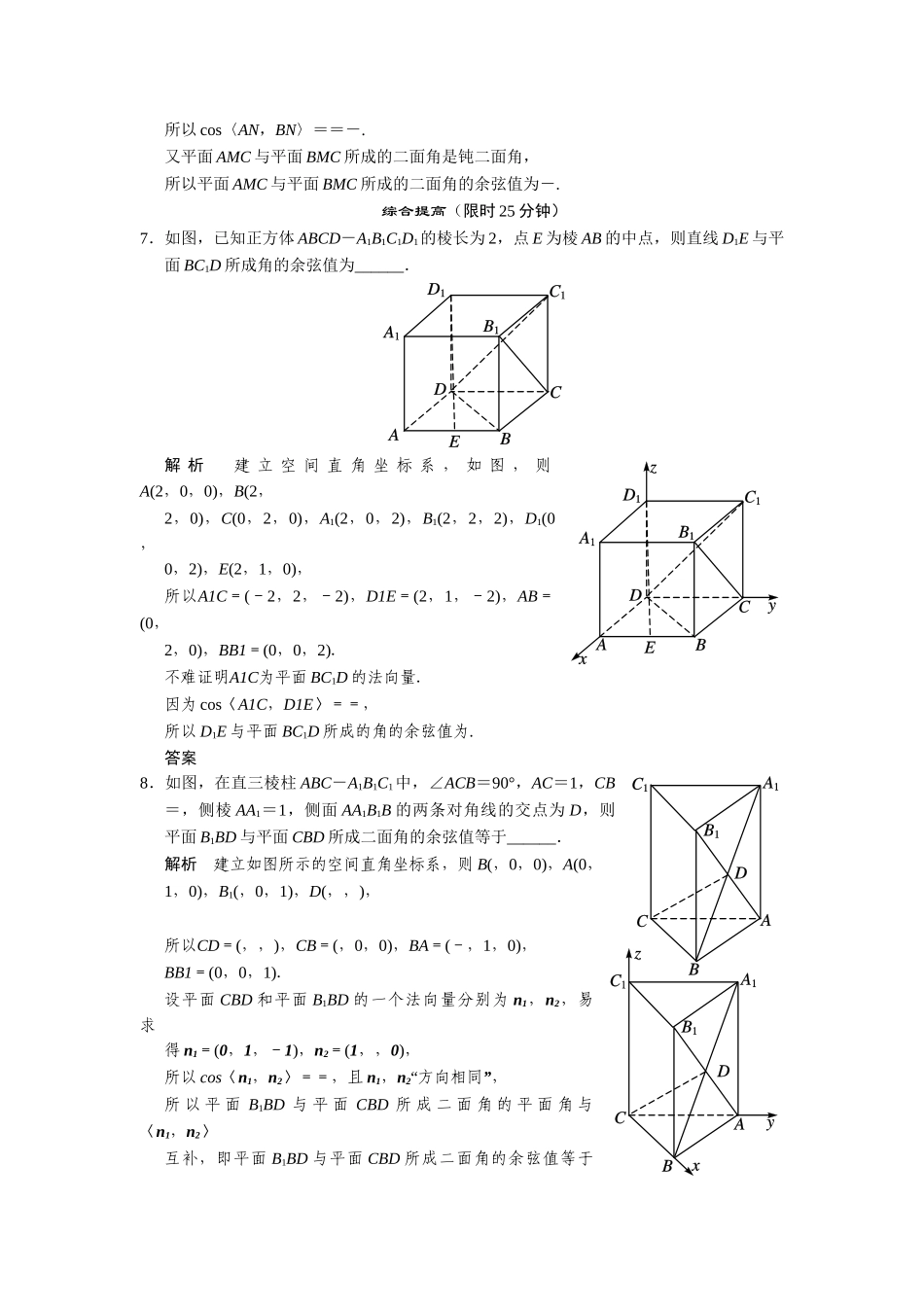
3.2.3空间角的计算双基达标限时20分钟1.若a=(1,λ,2),b=(2,-1,2),且a与b的夹角的余弦值为,则λ等于______.解析由cos〈a,b〉===,化简得55λ2+108λ-4=0,解得λ=-2或.答案-2或2.在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别为A1B1和BB1的中点,那么异面直线AM与CN所成角的余弦值为________.解析如图所示,建立空间直角坐标系,则A(1,0,0),M(1,,1),C(0,1,0),N(1,1,).∴AM=(0,,1),CN=(1,0,).∴AM·CN=,|AM|==|CN|.∴cos〈AM,CN〉==.答案3.在正方体ABCD-A1B1C1D1中,P是棱AD的中点,则二面角A1-BD1-P的正弦值为______.解析建立如图所示的空间直角坐标系,设正方体的棱长为1.容易求得平面A1B1D的一个法向量为n1=(-1,0,1),平面PB1D的一个法向量为n2=(0,-1,1)所以cos〈n1,n2〉==,且二面角A1-BD1-P是锐二面角,所以其正弦值为.答案4.在正方体ABCD-A1B1C1D1中,二面角D1-AC-D的正切值为______.解析建立如图所示的空间直角坐标系,设正方体的棱长为1.容易求得平面ACD1的一个法向量为n1=(1,-1,1),平面ACD的一个法向量为n2=(0,0,1),所以cos〈n1,n2〉==,且二面角D1-AC-D是锐二面角,所以其正弦值为,余弦值为,正切值为.答案5.如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是________.解析建立如图所示的坐标系,设正三棱柱的棱长为1,则B(,-,0),M(,,),B1(,-,1),因此AB1=(,-,1),BM=(0,1,),设异面直线AB1与BM所成的角为θ,则cosθ=|cos〈AB1,BM〉|==0,∴θ=90°.答案90°6.已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=AB=1,M是PB的中点.(1)证明:平面PAD⊥平面PCD;(2)求AC与PB所成的角的余弦值;(3)求平面AMC与平面BMC所成二面角的余弦值.解因为PA⊥AD,PA⊥AB,AD⊥AB,故以A为坐标原点AD长为单位长度,建立如图空间直角坐标系,则各点的坐标为A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,).(1)证明:因为AP=(0,0,1),DC=(0,1,0),故AP·DC=0,所以AP⊥DC.又由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,故由此得DC⊥平面PAD.又DC⊂平面PCD,故平面PAD⊥平面PCD.(2)因AC=(1,1,0),PB=(0,2,-1),故|AC|=,|PB|=,AC·PB=2,所以cos〈AC,PB〉==.由此得AC与PB所成的角的余弦值为.(3)在MC上取一点N(x,y,z),则存在λ,使NC=λMC.因为NC=(1-x,1-y,1-z),MC=(1,0,-),所以x=1-λ,y=1,z=λ.要使AN⊥MC,只需AN·MC=0即x-z=0,解得λ=.可知,当λ=时,N点的坐标为(,1,),能使AN·MC=0.此时,AN=(,1,),BN=(,-1,),有BN·MC=0.由AN·MC=0,BN·MC=0,得AN⊥MC,BN⊥MC,所以∠ANB为所求二面角的平面角.因为|AN|=,|BN|=,AN·BN=-,所以cos〈AN,BN〉==-.又平面AMC与平面BMC所成的二面角是钝二面角,所以平面AMC与平面BMC所成的二面角的余弦值为-.综合提高(限时25分钟)7.如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点,则直线D1E与平面BC1D所成角的余弦值为______.解析建立空间直角坐标系,如图,则A(2,0,0),B(2,2,0),C(0,2,0),A1(2,0,2),B1(2,2,2),D1(0,0,2),E(2,1,0),所以A1C=(-2,2,-2),D1E=(2,1,-2),AB=(0,2,0),BB1=(0,0,2).不难证明A1C为平面BC1D的法向量.因为cos〈A1C,D1E〉==,所以D1E与平面BC1D所成的角的余弦值为.答案8.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=,侧棱AA1=1,侧面AA1B1B的两条对角线的交点为D,则平面B1BD与平面CBD所成二面角的余弦值等于______.解析建立如图所示的空间直角坐标系,则B(,0,0),A(0,1,0),B1(,0,1),D(,,),所以CD=(,,),CB=(,0,0),BA=(-,1,0),BB1=(0,0,1).设平面CBD和平面B1BD的一个法向量分别为n1,n2,易求得n1=(0,1,-1),n2=(1,,0),所以cos〈n1,n2〉==,且n1,n2“方向相同”,所以平...