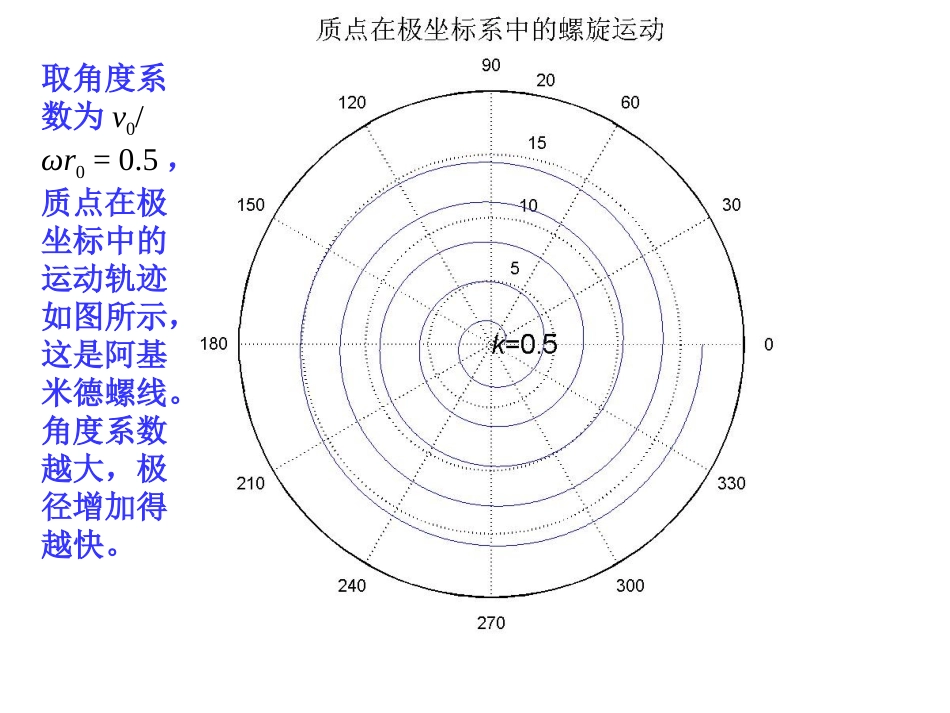
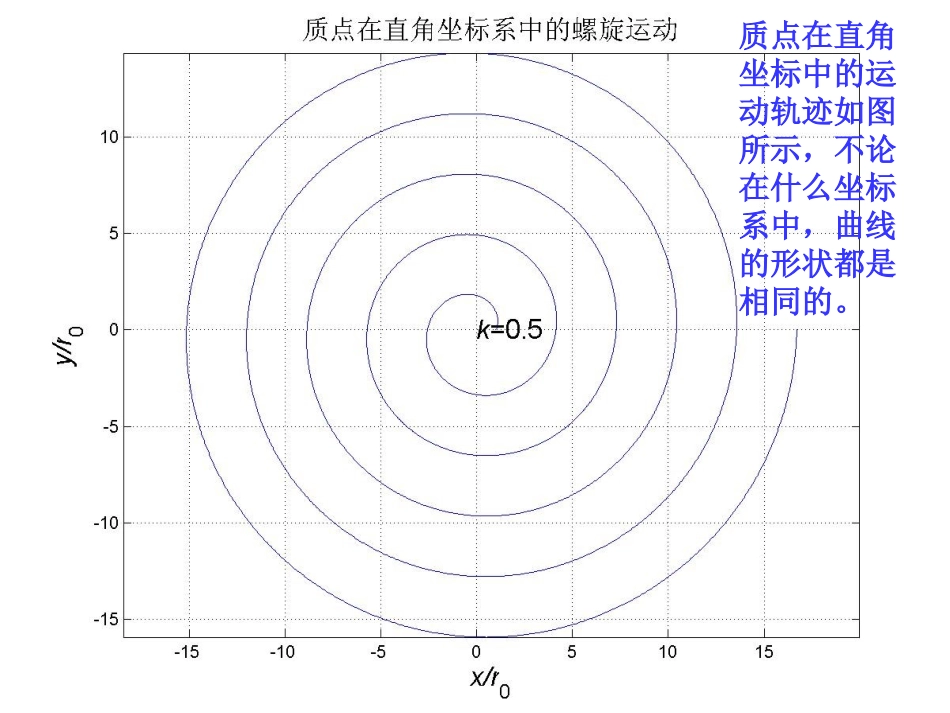
一质点的运动方程为r=r0+v0t,θ=ωt,式中r0,v0和ω是正常数。质点的运动轨迹是什么?质点的速度随时间如何变化?[解析]将第二式变形t=θ/ω,代入第一式得这是极坐标方程,质点轨迹是螺旋线。极坐标与直角坐标的转化公式是x=rcosθ,y=rsinθ,{范例1.4}质点的螺旋运动质点的径向速度为可知:质点速度的径向分量为常数,v0是极径增加的速率。质点的角向速度为00vrr0ddrrvvt00d()dvrrrvtt可见:速度的角向分量随时间线性增加。质点的合速度的大小为2222000[()]rvvvvrvt可知:质点的合速度大小将随时间增加。取角度系数为v0/ωr0=0.5,质点在极坐标中的运动轨迹如图所示,这是阿基米德螺线。角度系数越大,极径增加得越快。质点在直角坐标中的运动轨迹如图所示,不论在什么坐标系中,曲线的形状都是相同的。径向速度是一个常量,角向速度随时间直线增加,合速度也随时间增加。时间越长,质点的角向速度就越大,合速度与角向速度就越接近。质点运动时间越长,合速度就越大,这是由于角向速度不断增加的结果。