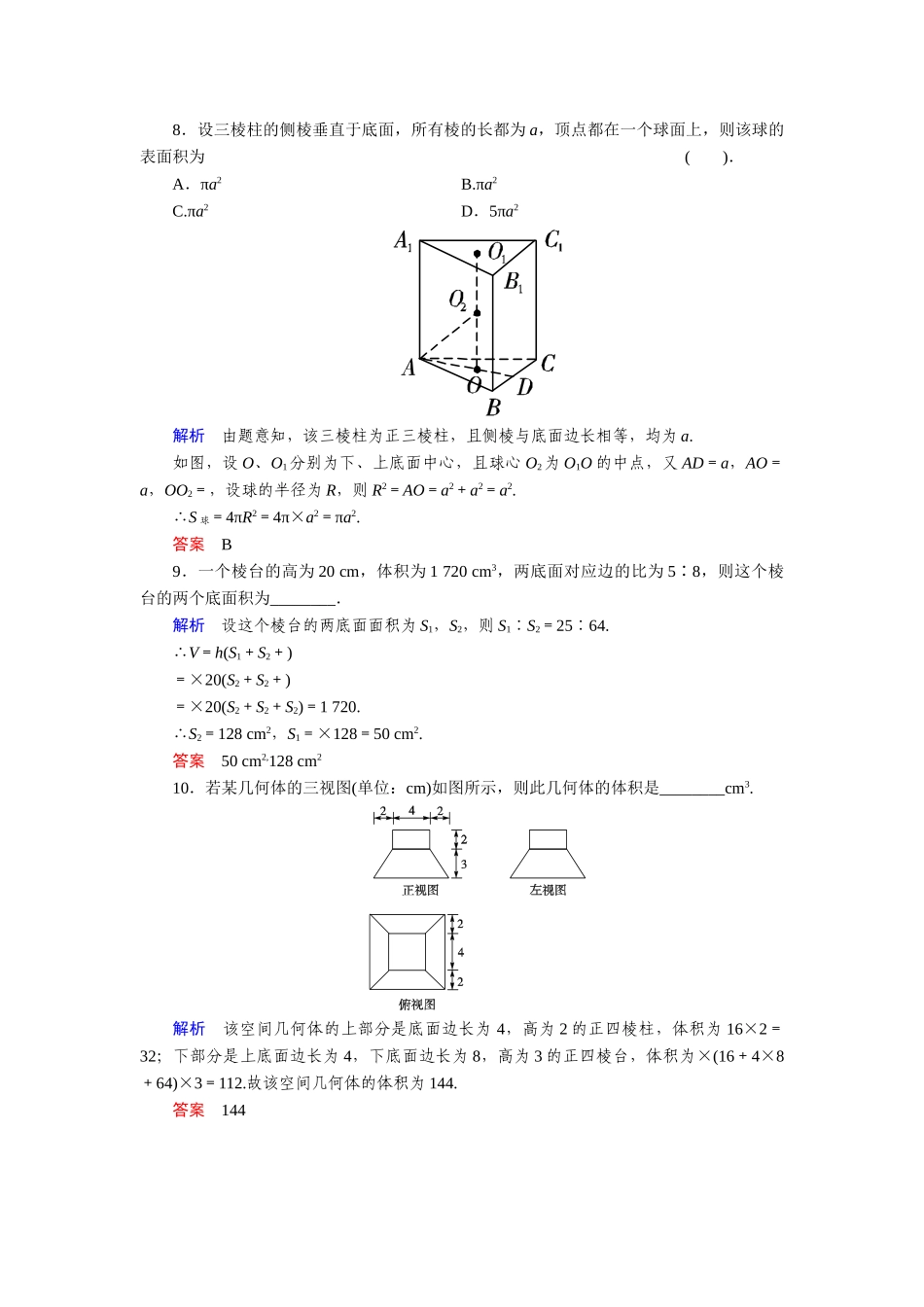
【创新设计】-学年高中数学6.1.3面积和体积公式活页训练湘教版必修31.一个正方体的表面积为6,并且正方体的各个顶点都在一个球面上,则此球的体积为().A.B.C.πD.解析设正方体的边长为a,球的半径为R,则6a2=6,∴a=1,∴2R=,即R=V=πR3=π×=π答案D2.正方体的八个顶点中有四个恰为正四面体的顶点,则正方体的全面积与正四面体的全面积之比为().A.B.C.D.解析设正方体棱长为a,S正方体全=6a2,而正四面体的棱长为a,S正四面体全=4·(a)2=2a2,∴==.答案B3.底面是菱形的直棱柱,它的体对角线的长分别是9和15,高是5,则这个棱柱的侧面面积是().A.130B.140C.150D.160解析如右图,直棱柱ABCD—A1B1C1D1,AA1=BB1=CC1=DD1=5,BD1=9,A1C=15,可求得AC==10,BD==2.所以AB=BC=C1B1=A1B1==8.所以棱柱侧面积为4×5×8=160.答案D4.一个球的表面积扩大为原来的3倍,那么该球的体积扩大为原来的________倍.解析球的表面积扩大为原来的3倍,则球的半径扩大为原来的倍,所以球的体积扩大为原来的()3=3倍.答案35.已知圆锥的高为4,母线长为5,则圆锥的侧面积为________.解析由题意知圆锥的底面半径r==3.∴S侧=×2π×3×5=15π.答案15π6.在球中有相距9cm的两个平行截面,它们的面积分别为49πcm2和400πcm2,求球的表面积.解(1)当球心在两截面同侧时,如图甲,由球的截面性质知,AO1∥BO2,且O1,O2分别为两截面圆的圆心,则OO1⊥AO1,OO2⊥BO2,设球的半径为R,∵π·O2B2=49π,∴O2B=7(cm).同理π·O1A2=400π,∴O1A=20(cm)设OO1=xcm,则OO2=(x+9)cm在Rt△OO1A中,R2=x2+202在Rt△OO2B中,R2=(x+9)2+72,∴x2+202=72+(x+9)2,解得x=15.∴R=25(cm)∴S球=4πR2=2500π(cm2),∴球的表面积为2500πcm2.(2)当球心在两个截面之间时,如图乙所示.设OD=x,则OC=9-x.由题意得π·AC2=49π∴AC=7cm.同理可得BD=20cm.设球半径为R,则由题意得x2+202=R2=(9-x)2+72即x2+400=(9-x)2+49,此方程无正数解,即此种情况不可能.综上所述,所求球的表面积为2500πcm2.7.若圆锥的侧面展开图是圆心角为120°、半径为l的扇形,则这个圆锥的表面积与侧面积的比是().A.3∶2B.2∶1C.4∶3D.5∶3解析设圆锥底面圆的半径为r,则2πr=l×,∴r=,∴===.答案C8.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为().A.πa2B.πa2C.πa2D.5πa2解析由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为a.如图,设O、O1分别为下、上底面中心,且球心O2为O1O的中点,又AD=a,AO=a,OO2=,设球的半径为R,则R2=AO=a2+a2=a2.∴S球=4πR2=4π×a2=πa2.答案B9.一个棱台的高为20cm,体积为1720cm3,两底面对应边的比为5∶8,则这个棱台的两个底面积为________.解析设这个棱台的两底面面积为S1,S2,则S1∶S2=25∶64.∴V=h(S1+S2+)=×20(S2+S2+)=×20(S2+S2+S2)=1720.∴S2=128cm2,S1=×128=50cm2.答案50cm2,128cm210.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是________cm3.解析该空间几何体的上部分是底面边长为4,高为2的正四棱柱,体积为16×2=32;下部分是上底面边长为4,下底面边长为8,高为3的正四棱台,体积为×(16+4×8+64)×3=112.故该空间几何体的体积为144.答案14411.已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,左视图是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V;(2)求该几何体的侧面积S.解(1)由该几何体的俯视图、正视图、左视图可知,该几何体是四棱锥,且四棱锥的底面ABCD是边长为6和8的矩形,高VO=4,O点是AC与BD的交点.∴该几何体的体积V=×8×6×4=64.(2)如图所示,侧面VAB中,VE⊥AB,则VE===5,∴S△VAB=×AB×VE=×8×5=20.侧面VBC中,VF⊥BC,则VF===4.∴S△VBC=×BC×VF=×6×4=12,∴该几何体的侧面积S=2(S△VAB+S△VBC)=40+24.12.(创新拓展)一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm,求钢球的半径.解如图,设钢球的半径为R,得钢球的体积为V球=πR3.钢球被放入水中后,瓶里所装的水由8cm上升到8.5cm,可得水实际升高0.5cm.∴升高的水的体积V水=πr2×h=π×32×0.5=4.5π.∵V球=V水,∴πR3=4.5π,∴R3==,∴R==1.5(cm).故钢球的半径为1.5cm.