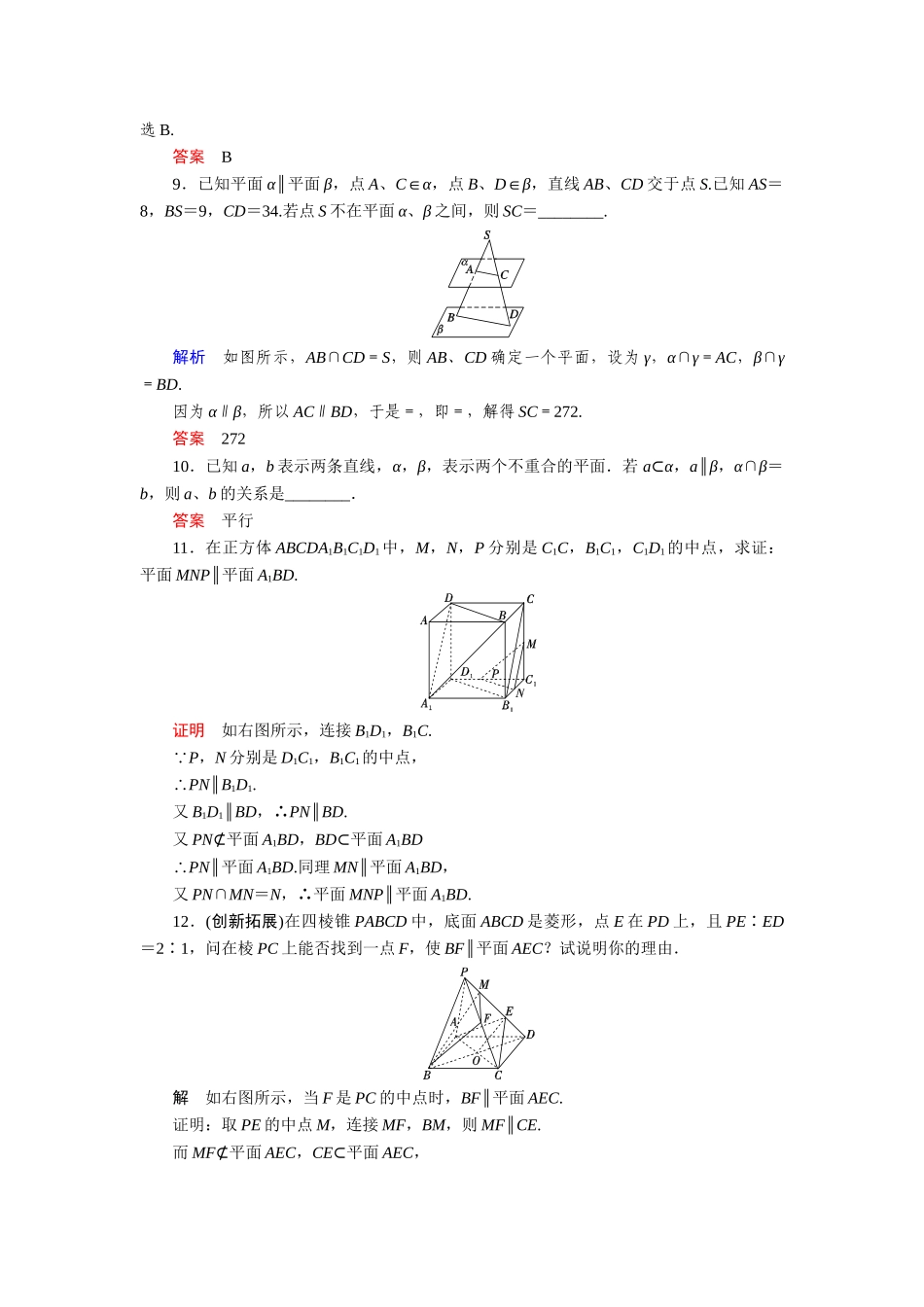
【创新设计】-学年高中数学6.2.2.2平面与平面的平行活页训练湘教版必修31.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是().A.一定平行B.一定相交C.平行或相交D.以上判断都不对解析可借助长方体模型来判断,两个平面可能平行也可能相交.答案C2.已知α、β是两个不重合的平面,在下列条件中,可确定α∥β的是().A.α、β都平行于直线lB.α内有三个不共线的点到β的距离相等C.l、m是α内两条直线,且l∥β,m∥βD.l、m是两条异面直线,且l∥β,m∥β,l∥α,m∥α解析在α内取一点A,过A作l1∥l,m1∥m,在β内取一点B,过B作l2∥l,m2∥m,则l1∥l2,m1∥m2,用面面平行的判定定理可得.答案D3.若α∥β,a⊂α,则下列四个命题中正确的是().①a与β内所有直线平行;②a与β内的无数条直线平行;③a与β内的任何一条直线都不垂直;④α与β无公共点.A.①②B.②④C.②③D.③④解析由性质知①错;由定义知②正确;因为a与β内直线可能异面垂直,故③错;由定义知④正确.故选B.答案B4.已知直线a与直线b,平面α与平面β满足下列关系,a∥α,b∥α,a⊂β,b⊂β,则α与β的位置关系是________.解析a∥α,b∥α,a⊂β,b⊂β,但是直线a与直线b的关系未确定,如果直线a与直线b平行,那么α与β可能相交或平行,如果直线a与直线b相交,那么α与β平行.答案平行或相交5.已知平面α∥β∥γ,两条直线l,m分别与平面α,β,γ相交于点A,B,C和D,E,F,已知AB=6,=,则AC=________.解析∵α∥β∥γ,∴=.由=,得=,∴=.而AB=6,∴BC=9,∴AC=AB+BC=15.答案156.如图所示,三棱柱ABCA1B1C1中,E是AC的中点.求证:AB1∥平面BEC1.证明取A1C1的中点F,连接AF,B1F,∵E为AC的中点,∴AF∥C1E.∵AF⊄平面BEC1,C1E⊂平面BEC1∴AF∥平面BEC1.由E、F分别是AC、A1C1的中点,EF綊AA1綊BB1,∴BE綊B1F.又∵B1F⊄平面BEC1,BE⊂平面BEC1∴B1F∥平面BEC1.∵B1F∩AF=F,∴平面BEC1∥平面AB1F.∵AB1⊂平面AB1F,∴AB1∥平面BEC1.7.P是三角形ABC所在平面外一点,平面α∥平面ABC,α交线段PA、PB、PC于A′、B′、C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC=().A.2∶25B.4∶25C.2∶5D.4∶5解析由面面平行的性质定理知,A′B′∥AB,A′B′∶AB=PA′∶PA=2∶5,所以S△A′B′C′∶S△ABC=4∶25.答案B8.已知m,n是两条直线,α,β是两个平面.有以下命题:①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;②若m∥α,m∥β,则α∥β;③若m∥α,n∥β,m∥n,则α∥β.其中正确命题的个数是().A.0B.1C.2D.3解析设m∩n=P,则直线m,n可确定一个平面,设为γ,由面面平行的判定定理知,α∥γ,β∥γ,因此,α∥β,即命题①正确;在长方体ABCDA1B1C1D1中,C1D1∥平面ABCD,C1D1∥平面ABB1A1,但平面ABCD∩平面ABB1A1=AB,即满足命题②的条件,但平面ABCD与平面ADD1A1不平行,因此命题②不正确;同样可知,命题③也不正确.故选B.答案B9.已知平面α∥平面β,点A、C∈α,点B、D∈β,直线AB、CD交于点S.已知AS=8,BS=9,CD=34.若点S不在平面α、β之间,则SC=________.解析如图所示,AB∩CD=S,则AB、CD确定一个平面,设为γ,α∩γ=AC,β∩γ=BD.因为α∥β,所以AC∥BD,于是=,即=,解得SC=272.答案27210.已知a,b表示两条直线,α,β,表示两个不重合的平面.若a⊂α,a∥β,α∩β=b,则a、b的关系是________.答案平行11.在正方体ABCDA1B1C1D1中,M,N,P分别是C1C,B1C1,C1D1的中点,求证:平面MNP∥平面A1BD.证明如右图所示,连接B1D1,B1C.∵P,N分别是D1C1,B1C1的中点,∴PN∥B1D1.又B1D1∥BD,∴PN∥BD.又PN⊄平面A1BD,BD⊂平面A1BD∴PN∥平面A1BD.同理MN∥平面A1BD,又PN∩MN=N,∴平面MNP∥平面A1BD.12.(创新拓展)在四棱锥PABCD中,底面ABCD是菱形,点E在PD上,且PE∶ED=2∶1,问在棱PC上能否找到一点F,使BF∥平面AEC?试说明你的理由.解如右图所示,当F是PC的中点时,BF∥平面AEC.证明:取PE的中点M,连接MF,BM,则MF∥CE.而MF⊄平面AEC,CE⊂平面AEC,∴MF∥平面AEC.连接BD交AC于O,连接OE,则由四边形ABCD是菱形知O是BD的中点.由已知PE∶ED=2∶1,M是PE的中点知E是MD的中点.∴OE∥BM.而BM⊄平面AEC,OE⊂平面AEC,∴BM∥平面AEC.又∵MF∩BM=M,∴平面BMF∥平面AEC.而BF⊂平面BMF,∴BF∥平面AEC.