用解析法设计四杆机构VIP免费

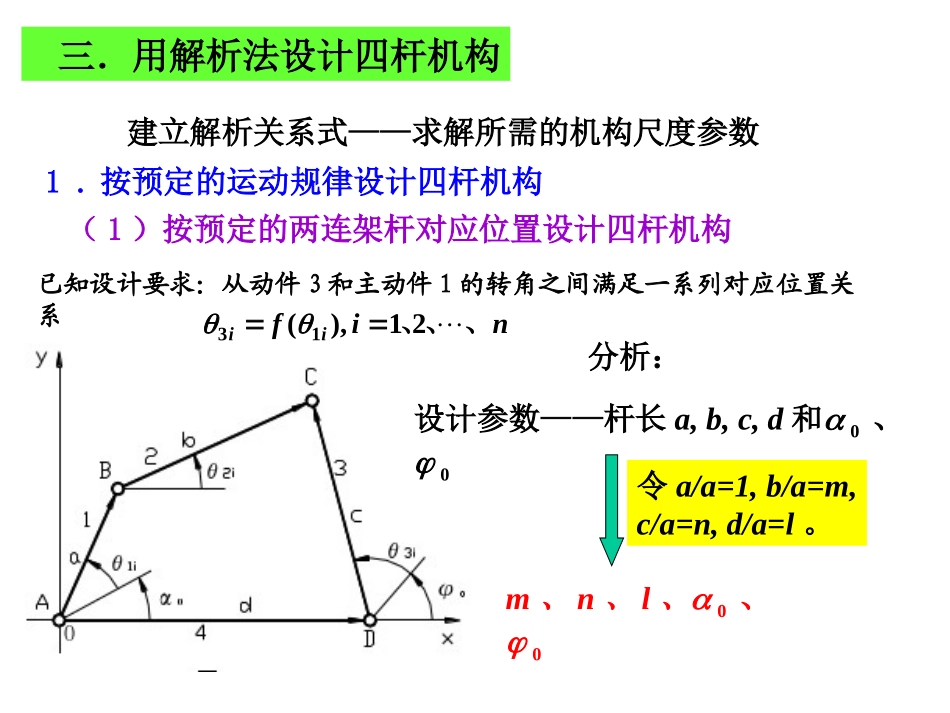
三．用解析法设计四杆机构建立解析关系式——求解所需的机构尺度参数1.按预定的运动规律设计四杆机构（1）按预定的两连架杆对应位置设计四杆机构已知设计要求：从动件3和主动件1的转角之间满足一系列对应位置关系nifii、、、21),(13分析：设计参数——杆长a,b,c,d和0、0令a/a=1,b/a=m,c/a=n,d/a=l。m、n、l、0、0建立直角坐标系，并标出各杆矢，写出矢量方程向x、y轴投影，得)sin(sin)sin()cos(cos)cos(0320103201iiiiiicbacdbacdba将相对长度代入上式，并移项，得)sin()sin(sin)cos()cos(cos0103201032iiiiiinmnlm将等式两边平方和，消去2i，并整理得)2/()1()cos()/()cos()cos(22201030301lmnllnniiiiP2P1P020103103001)cos()cos()cos(PPPiiii将两连架杆的已知对应角代入上式，列方程组求解注意：方程共有5个待定参数，根据解析式可解条件：★当两连架杆的对应位置数N=5时，可以实现精确解。★当N5时，不能精确求解，只能近似设计。★当N5时，可预选尺度参数数目N0=5-N，故有无穷多解。注意：N=4或5时，方程组为非线性例题：试设计如图所示铰链四杆机构，要求其两连架杆满足如下三组对应位置关系：11=45o,31=50o,12=90o,32=80o,13=135o,33=110o。分析：N=3则N0=2，常选0=0=0o求解：将三组对应位置值代入解析式得：200100020010002001000)135110cos(110cos135cos)9080cos(80cos90cos)4550cos(50cos45cosPPPPPPPPPP0=1.533P1=-1.0628P2=0.7805)2/()1()/(222310lmnlPlnPnPn=1.533l=1.442m=1.783根据结构要求，确定曲柄长度，可求各构件实际长度。（2）按预期函数设计四杆机构★期望函数：要求四杆机构两连架杆转角之间实现的函数关系y=f(x)。★再现函数：连杆机构实际实现的函数y=F(x)。★设计方法——插值逼近法（1）插值结点：再现函数和期望函数曲线的交点（2）插值逼近法：按插值结点的值来设计四杆机构（3）用插值逼近法设计四杆机构的作法在给定自变量x0~xm区间内选取结点，则有f(x)=F(x)将结点对应值转化为两连架杆的对应转角代入解析方程式，列方程组求解未知参数（4）插值结点的选取在结点处应有f(x)-F(x)=0结点以外的其他位置的偏差为0)()(xFxfy结点数：最多为5个结点位置的分布根据函数逼近理论按下式选取：偏差大小取决结点数目偏差大小取决结点数目和分布位置和分布位置2/)])/(21(2)cos[180(-)/2(00mixxxxxmmii=1、2、……、m;m为插值结点总数。例题：如图所示，设两连架杆转角之间的对应函数关系为y=logx,1x2,其设计步骤如下：1）根据已知条件x0=1，xm=2；可求得y0=logx0=0，ym=logxm=0.301。2）根据经验取主、从动件的转角范围分别为αm=60°,φm=90°,则自变量和函数与转角的比例分别为60/1/)(0mmxx90/301.0/)(0mmyy3）由式（6-16）求插值结点处的自变量（设总数m=3），则x1=(2+1)/2-(2-1)cos[180°(2×1-1)/(2×3)]/2=1.067；x2=1.500；x3=1.933求结点处的函数值y1=log1.067=0.0282；y2=0.1761；y3=0.2862求主、从动件在结点处的相应转角4）试取初始角α0=86°，φ0=23.5°(一般α0及φ0不同时为零)。5）将各结点的坐标值及初始角代入式57.85,98.5565.52,3043.8/)(,02.4/)(33220110011yyxx20103103001)cos()cos()cos(PPPiiiicos90.02°=P0cos31.93°+P1cos58.09°+P2cos116°=P0cos76.15°+P1cos39.85°+P2cos141.98°=P0cos109.07°+P1cos32.91°+P2得解得P0=0.568719，P1=-0.382598，P2=-0.2807826）求机构各构件相对长度为a=1，b=2.0899，c=0.56872，d=1.48657）检验偏差值Δφ消去2，并将变量符号2换为，3换为，得b2=a2+d2+c2+2cdcos(φ+φ0)-2adcos(α+α0)-2accos[(α+α0)-(φ+φ0)]令A=sin（+0)B=cos（+0)...