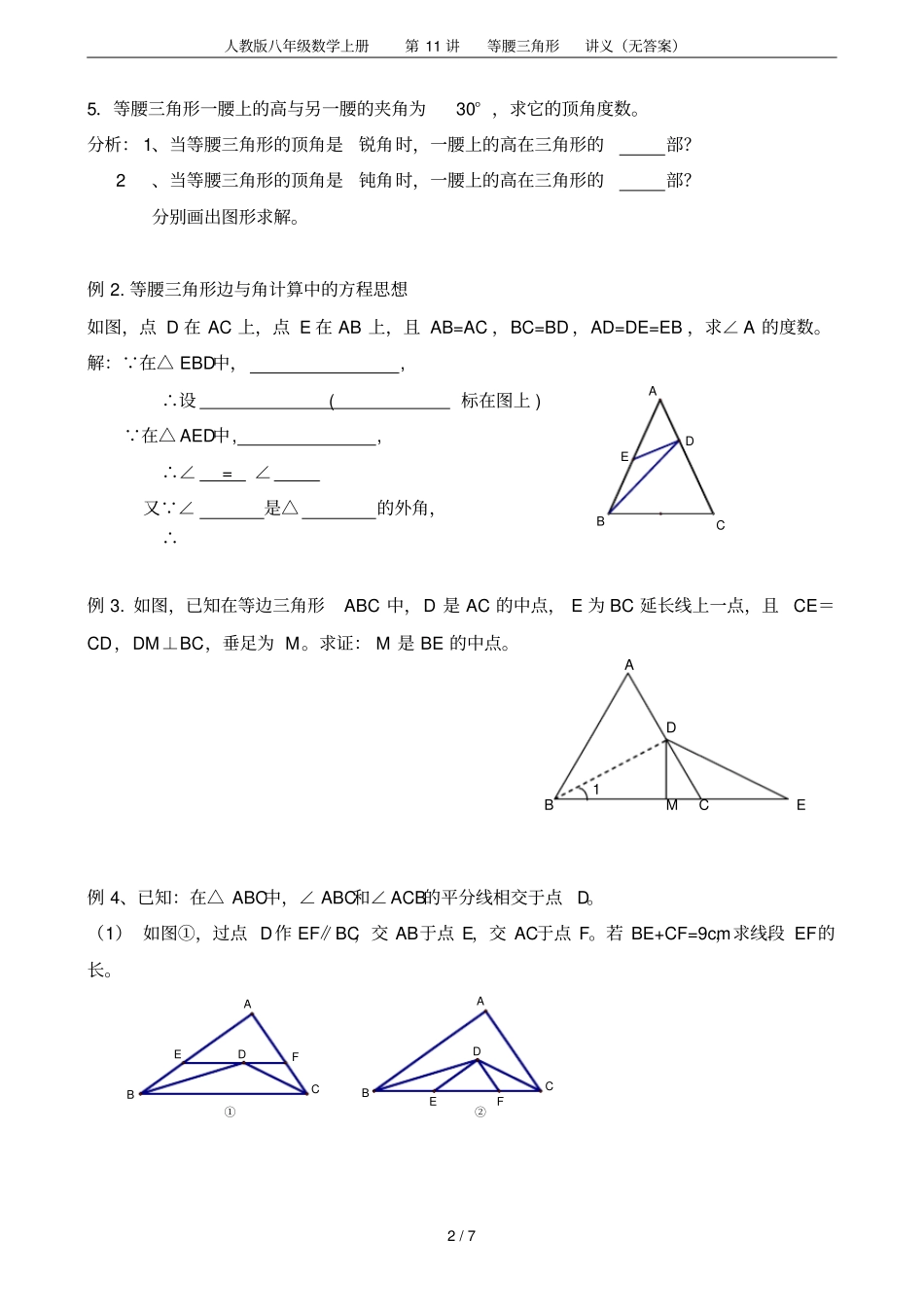
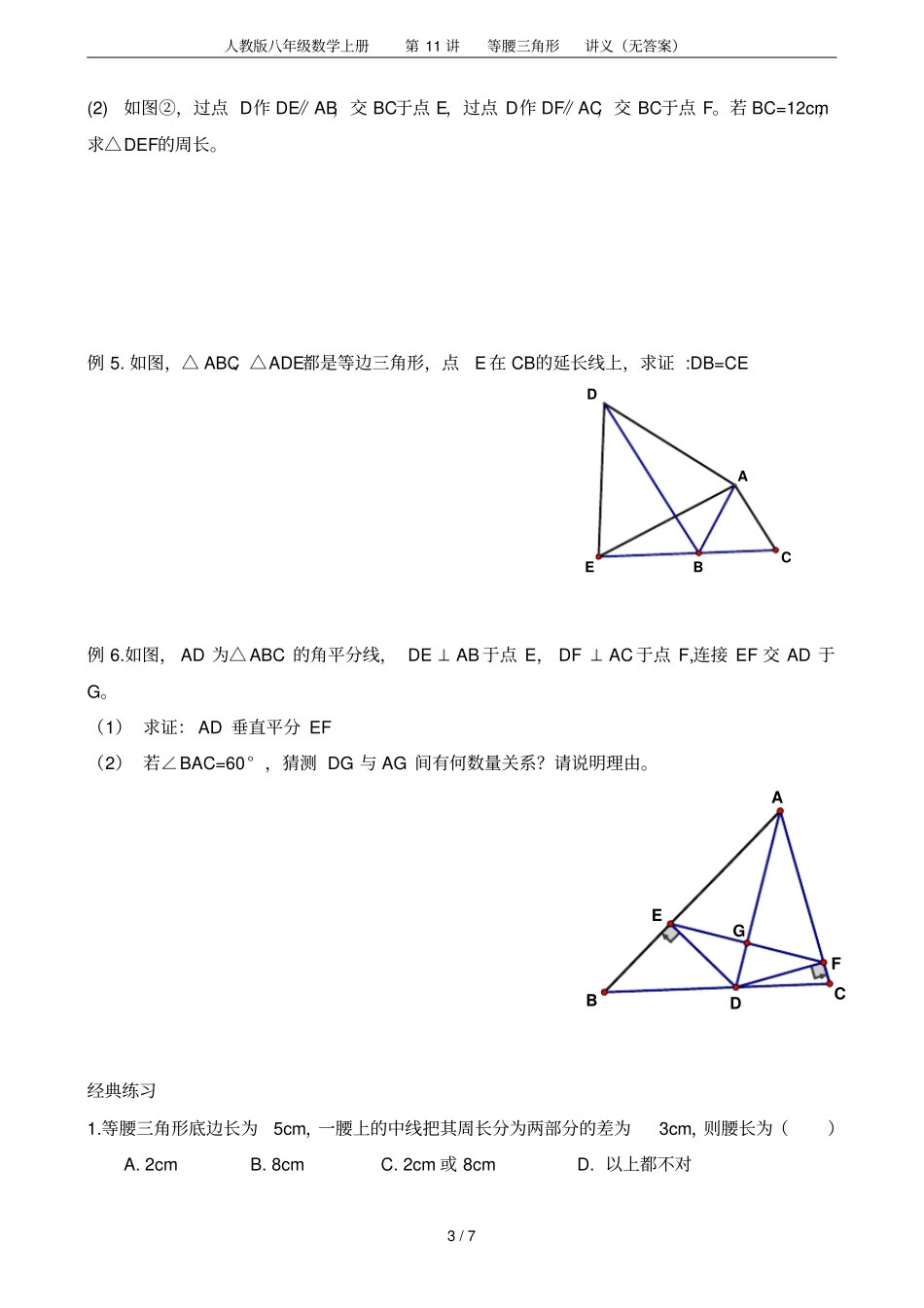
人教版八年级数学上册第11讲等腰三角形讲义(无答案)1/7第11讲等腰三角形知识点梳理:(一)等腰三角形的性质等腰三角形的定义:腰、底边、顶角、底角。定理:等腰三角形的两个底角相等(简写成“等边对等角”)。推论1:等腰三角形顶角的平分线平分底边并且垂直于底边,这就是说,等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(通常称作“三线合一”)。推论2:等边三角形的各角都相等,并且每一个角都等于60°。等腰三角形是以底边的垂直平分线为对称轴的轴对称图形;(二)等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”。)推论1:三个角都相等的三角形是等边三角形(有两个角是60°的三角形是等边三角形)。推论2:有一个角等于60°的等腰三角形是等边三角形。推论3:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。(三)方法点拨:等腰三角形中常用的辅助线等腰三角形顶角平分线、底边上的高、底边上的中线常常作为解决有关等腰三角形问题的辅助线,由于这条线可以把顶角和底边折半,所以常通过它来证明线段或角的倍分问题,在等腰三角形中,虽然顶角的平分线、底边上的高、底边上的中线互相重合,添加辅助线时,有时作哪条线都可以,有时需要作顶角的平分线,有时则需要作高或中线,这要视具体情况来定。经典例题:例1.等腰三角形边与角计算中的分类讨论思想1.已知等腰三角形的一个内角是1000,则它的另外两个内角是2.已知等腰三角形的周长为24,一边长为10,则另外两边的长是3.等腰三角形的两边长是6和7,则三角形的周长为:*4.一等腰三角形一腰上的中线把这个三角形的周长分成15cm和18cm两部分,则这个等腰三角形的底边长是人教版八年级数学上册第11讲等腰三角形讲义(无答案)2/75.等腰三角形一腰上的高与另一腰的夹角为30°,求它的顶角度数。分析:1、当等腰三角形的顶角是锐角时,一腰上的高在三角形的部?2、当等腰三角形的顶角是钝角时,一腰上的高在三角形的部?分别画出图形求解。例2.等腰三角形边与角计算中的方程思想如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数。解: 在△EBD中,,∴设(标在图上) 在△AED中,,∴∠=∠又 ∠是△的外角,∴例3.如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC,垂足为M。求证:M是BE的中点。例4、已知:在△ABC中,∠ABC和∠ACB的平分线相交于点D。(1)如图①,过点D作EF∥BC,交AB于点E,交AC于点F。若BE+CF=9cm,求线段EF的长。②①FEFEBCAACBDDAD1BMCECABDE人教版八年级数学上册第11讲等腰三角形讲义(无答案)3/7DAECBGFEDABC(2)如图②,过点D作DE∥AB,交BC于点E,过点D作DF∥AC,交BC于点F。若BC=12cm,求△DEF的周长。例5.如图,△ABC、△ADE都是等边三角形,点E在CB的延长线上,求证:DB=CE例6.如图,AD为△ABC的角平分线,ABDE于点E,ACDF于点F,连接EF交AD于G。(1)求证:AD垂直平分EF(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由。经典练习1.等腰三角形底边长为5cm,一腰上的中线把其周长分为两部分的差为3cm,则腰长为()A.2cmB.8cmC.2cm或8cmD.以上都不对人教版八年级数学上册第11讲等腰三角形讲义(无答案)4/7EDCAB2.如图,△ABC中,AB=AC,∠A=36°,BD、CE分别为∠ABC与∠ACB的角平分线,且相交于点F,则图中的等腰三角形有()A.6个B.7个C.8个D.9个3.如图,ABC是等边三角形,BCBD90CBD,,则1的度数是________。4.已知:如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,E、F分别是垂足。求证:AE=AF。5.ABC中,120AACAB,,AB的中垂线交AB于D,交CA延长线于E,求证:BC21DE。EDCAB6.如图,ABC中,AB=AC,EAEDBDBC,求∠A的度数.AEFBDCCA1DB23A36°EDFBC人教版八年级数学上册第11讲等腰三角形讲义(无答案)5/7DCABEFPQCABDEDCAB21EFDCBA7.如图,在Rt△ABC中,∠BAC=90°,∠B=30°,BC=8,AD⊥BC于点D,则DC=能力提高1、如图,过ABC的顶点A的直线DE∥BC,ABC、ACB的平分线分别交DE于E、D两点,若6AB,8BC,则DE可能...