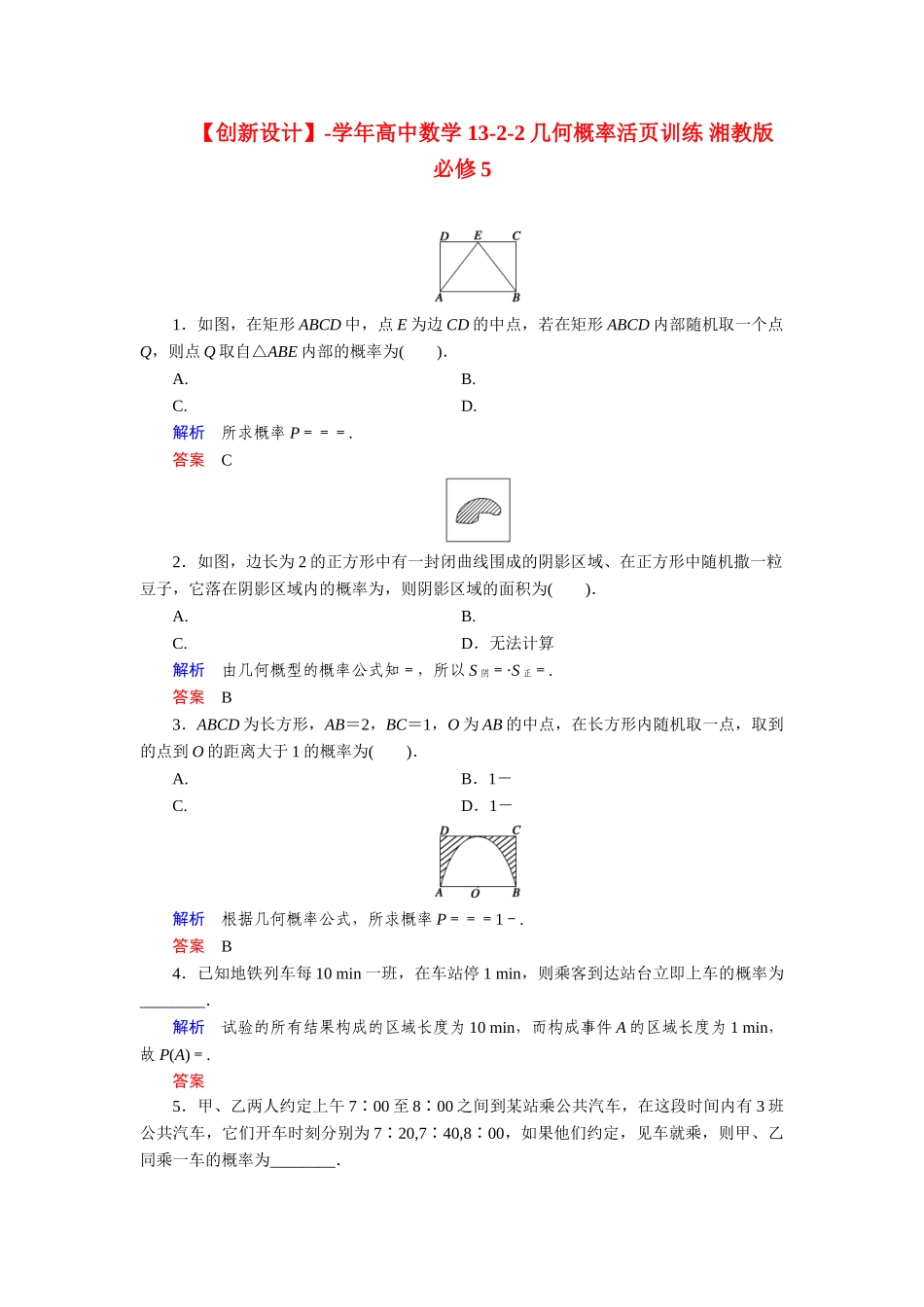
【创新设计】-学年高中数学13-2-2几何概率活页训练湘教版必修51.如图,在矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率为().A.B.C.D.解析所求概率P===.答案C2.如图,边长为2的正方形中有一封闭曲线围成的阴影区域、在正方形中随机撒一粒豆子,它落在阴影区域内的概率为,则阴影区域的面积为().A.B.C.D.无法计算解析由几何概型的概率公式知=,所以S阴=·S正=.答案B3.ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形内随机取一点,取到的点到O的距离大于1的概率为().A.B.1-C.D.1-解析根据几何概率公式,所求概率P===1-.答案B4.已知地铁列车每10min一班,在车站停1min,则乘客到达站台立即上车的概率为________.解析试验的所有结果构成的区域长度为10min,而构成事件A的区域长度为1min,故P(A)=.答案5.甲、乙两人约定上午7∶00至8∶00之间到某站乘公共汽车,在这段时间内有3班公共汽车,它们开车时刻分别为7∶20,7∶40,8∶00,如果他们约定,见车就乘,则甲、乙同乘一车的概率为________.解析如图,设甲到达汽车站的时刻为x,乙到达汽车站的时刻为y,则7≤x≤8,7≤y≤8,即甲乙两人到达汽车站的时刻(x,y)所对应的区域在平面直角坐标系中画出(如图所示)是大正方形.将三班车到站的时刻在图形中画出,则甲乙两人要想乘同一班车,必须满足7≤x≤7,7≤y≤7;7≤x≤7,7≤y≤7;7≤x≤8,7≤y≤8.即(x,y)必须落在图形中的三个带阴影的小正方形内,所以由几何概率的计算公式得:P==.答案6.射箭比赛的箭靶涂有五个彩色的圆环,从外向内为白色、黑色、蓝色、红色,靶心为金色.金色靶心叫“黄心”.奥运会的比赛靶面直径为122cm,靶心直径为12.2cm.运动员在70m外射箭.假设射箭都能中靶,且射中靶面内任一点都是等可能的,那么射中黄心的概率为多少?解把射中靶面看成一次试验,其结果可以是靶面直径为122cm的大圆内的任意一点,有无限个,属于几何概型.设“射中黄心”为事件A.全部结果构成的区域面积是×π×1222cm2,事件A的结果构成的区域面积是×π×12.22cm2,则P(A)==0.01,即射中黄心的概率为0.01.7.一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒.当你到达路口时,看见红灯、黄灯与不看见红灯的三种情况的概率依次是().A.,,B.,,C.,,D.,,解析测度为长度的几何概型,分别为=,=,=.答案A8.如图,靶子由三个半径为R,2R,3R的同心圆组成,如果你向靶子内随机地掷一支飞镖,命中区域Ⅰ、Ⅱ、Ⅲ的概率分别为p1,p2,p3,则p1∶p2∶p3=().A.1∶3∶5B.1∶2∶5C.2∶3∶4D.2∶2∶5解析p1∶p2∶p3=πR2∶(π×4R2-πR2)∶(π×9R2-π×4R2)=1∶3∶5.答案A9.在如图所示的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆中的概率为________.解析P==.(正方形的边长为2).答案10.已知Ω={(x,y)|x+y≤6,x≥0,y≥0},A={(x,y)|x≤4,y≥0,x-2y≥0},若向区域Ω内随机投一点P,则点P落在区域A内的概率为________.解析如图,在平面直角坐标系中,分别作出Ω,A表示的平面区域结合图象,所求概率为P===.答案11.某同学到公共汽车站等车上学,可乘坐8路、23路公共汽车,其中8路车每10分钟一班,23路车每15分钟一班,求这位同学等车不超过8分钟的概率.解把该同学的到站时间看做原点O,设x分钟后23路车到站,则0≤x≤15;设y分钟后8路车到站,则0≤y≤10,如右图.记“8分钟内乘坐8路车或23路车”为事件A,则A所占区域面积为8×8+2×8+7×8=136,整个区域的面积为10×15=150,∴P(A)=≈0.91.那么,等车不超过8分钟的概率约为0.91.12.(创新拓展)有一条长为2的线段,(1)在平面内任取两点,求它们到线段中点距离平方和小于1的概率;(2)在空间内任取三点,求它们到线段中点距离平方和小于1的概率.解(1)设线段上两点到线段中点的距离分别为|x|,|y|,记“它们到中点距离平方和小于1”为事件A,则事件A={(x,y)|x2+y2<1}.由于|x|≤1,|y|≤1,因此P(A)==,即它们到中点距离平方和小于1的概率为.(2)设线段上三点到线段中点的距离分别为|x|,|y|,|z|,记“它们到中点距离平方和小于1”为事件B,则事件B={(x,y,z)|x2+y2+z2<1}.由于|x|≤1,|y|≤1,|z|≤1,因此P(B)==,即它们到中点距离平方和小于1的概率为.