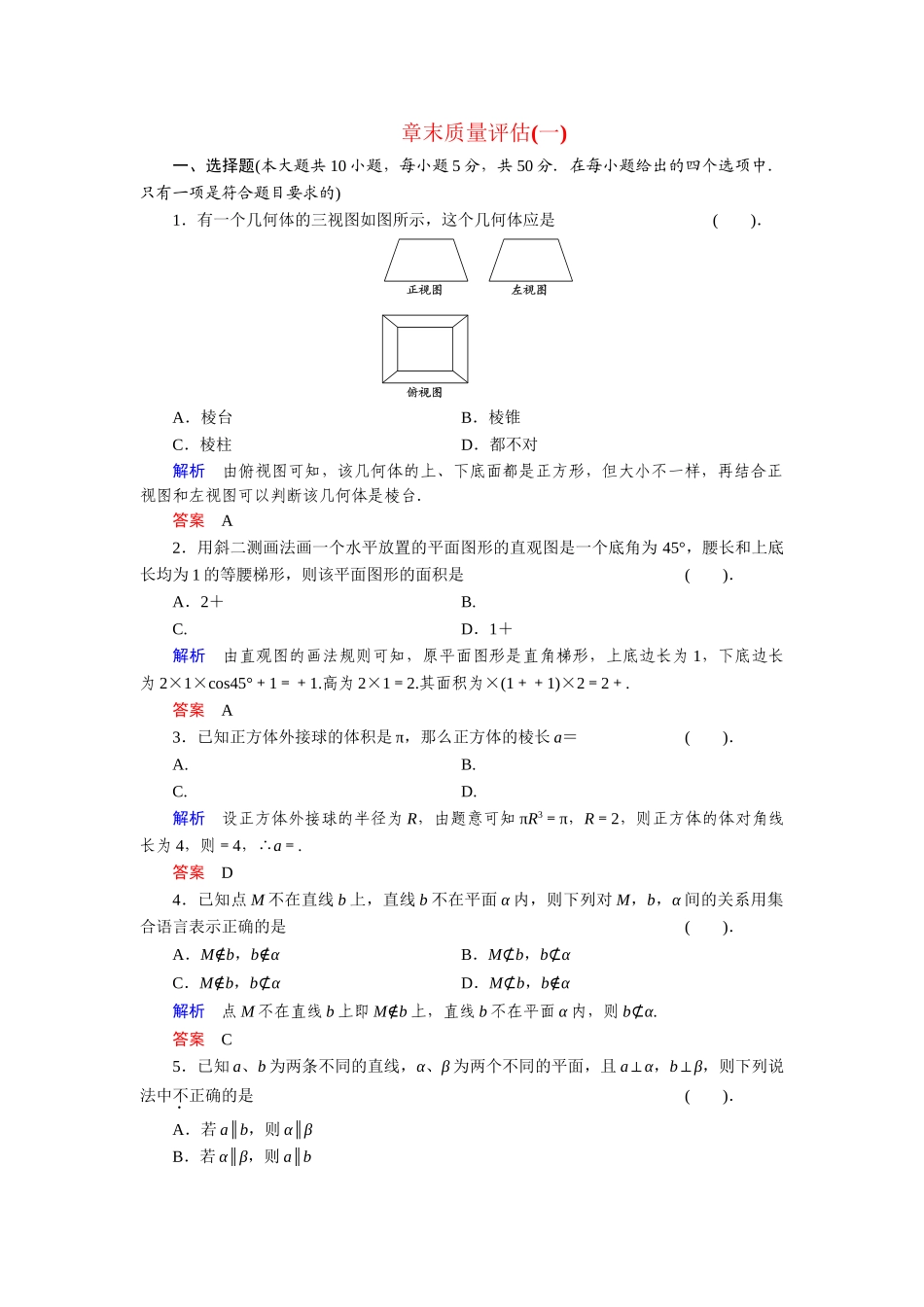
章末质量评估(一)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中.只有一项是符合题目要求的)1.有一个几何体的三视图如图所示,这个几何体应是().A.棱台B.棱锥C.棱柱D.都不对解析由俯视图可知,该几何体的上、下底面都是正方形,但大小不一样,再结合正视图和左视图可以判断该几何体是棱台.答案A2.用斜二测画法画一个水平放置的平面图形的直观图是一个底角为45°,腰长和上底长均为1的等腰梯形,则该平面图形的面积是().A.2+B.C.D.1+解析由直观图的画法规则可知,原平面图形是直角梯形,上底边长为1,下底边长为2×1×cos45°+1=+1.高为2×1=2.其面积为×(1++1)×2=2+.答案A3.已知正方体外接球的体积是π,那么正方体的棱长a=().A.B.C.D.解析设正方体外接球的半径为R,由题意可知πR3=π,R=2,则正方体的体对角线长为4,则=4,∴a=.答案D4.已知点M不在直线b上,直线b不在平面α内,则下列对M,b,α间的关系用集合语言表示正确的是().A.M∉b,b∉αB.M⊄b,b⊄αC.M∉b,b⊄αD.M⊄b,b∉α解析点M不在直线b上即M∉b上,直线b不在平面α内,则b⊄α.答案C5.已知a、b为两条不同的直线,α、β为两个不同的平面,且a⊥α,b⊥β,则下列说法中不正确的是().A.若a∥b,则α∥βB.若α∥β,则a∥bC.若a,b相交,则α、β相交D.若α,β相交,则a、b相交解析若a⊥α,b⊥β,α、β相交,则a,b相交或异面,故D不正确.答案D6.圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面的半径为().A.7B.6C.5D.3解析设圆台的上,下底面半径为r,R,则2πR=3·2πr,∴R=3r.又π(R+r)·l=84π,∴π(3r+r)·3=84π,∴r=7.答案A7.设有直线m、n和平面α、β.下列四个说法中,正确的是().A.若m∥α,m⊥n则n⊥αB.若m⊂α,n⊂α,m∥β,n∥β,则α∥βC.若α⊥β,m⊂α,则m⊥βD.若α⊥β,m⊥β,m⊄α,则m∥α解析由线面平行和线面垂直的判定可知,A、B、C错误,D正确.答案D8.已知一空间几何体的三视图如图所示,则该几何体的体积为().A.πcm3B.3πcm3C.πcm3D.πcm3解析由三视图可知,此几何体是一个底面半径为1cm,高为3cm的圆柱的上部去掉一个半径为1cm的半球所形成的几何体,所以其体积为V=πr2h-πr3=3π-π=π(cm3).答案D9.对于平面α和直线m,n,下列命题是真命题的是().A.若m,n与α所成的角相等,则m∥nB.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n⊥α,则m⊥n解析若m、n与α所成角相等,则m与n平行、相交或异面,应排除A.若m∥α,n∥α,则m与n平行,相交或异面,应排除B;若m⊥α,m⊥n,则n∥α或n⊂α,应排除C.答案D10.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是().A.BC∥平面PDFB.DF⊥平面PAEC.平面PDE⊥平面ABCD.平面PDF⊥平面PAE解析如图所示,正四面体P-ABC中,因为DF∥BC,DF⊂平面PDF,BC⊄平面PDF,所以BC∥平面PDF,因此选项A正确;因为PB=PC,AB=AC,E是BC的中点,所以PE⊥BC,AC⊥BC,又AE∩PE=E,所以BC⊥平面PAE,又DF∥BC,所以DF⊥平面PAE,而DF⊂平面PDF,所以平面PDF⊥平面PAE,因此选项B、D都正确.答案C二、填空题(本大题共5小题,每小题5分,共25分.请把正确答案填在题中横线上)11.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,则四边形ABCD绕AD所在直线旋转一周所成几何体的表面积S=________,体积V=________.解析该几何体可以看成是由一个圆台(由梯形ABCE旋转得到)割去一个圆锥(由△CDE旋转得到)所构成的.设圆台的体积为V1,上、下底面面积分别为S1,S2,侧面积为S3,圆锥的体积为V2,侧面积为S4,由∠ADC=135°可得,∠CDE=45°,又CD=2,AD=2,AB=5,所以CE=2,DE=2,AE=4,BC=5,于是,几何体的表面积S=S2+S3+S4=π×52+π×(2+5)×5+π×2×2=(60+4)π,体积V=V1-V2=(S1++S2)×4-S1×2=π.答案(60+4)ππ12.一个正三棱柱(底面是正三角形,各个侧面均是矩形)的三视...