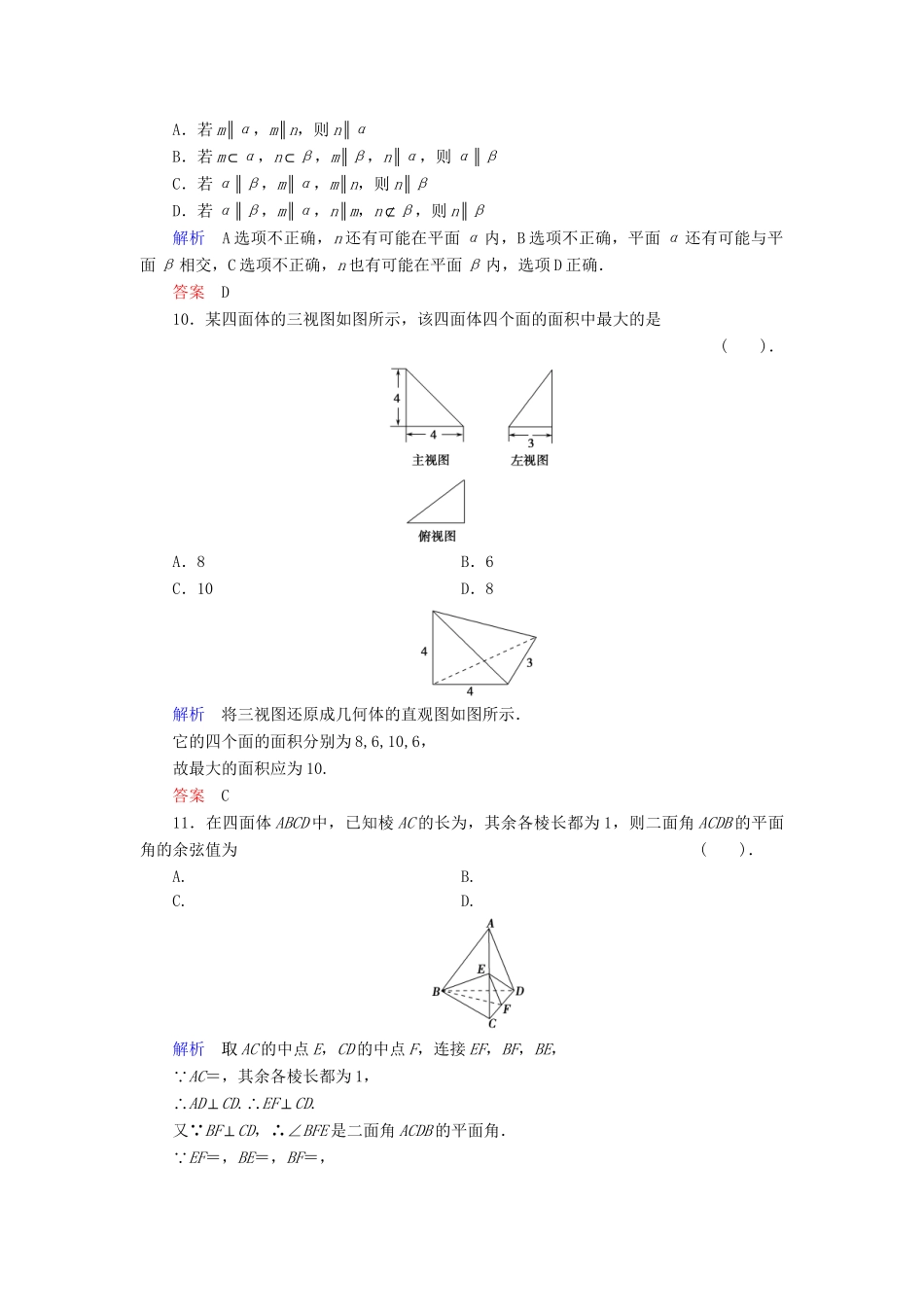
章末质量评估(一)(时间:90分钟满分:120分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.圆锥的高扩大到原来的2倍,底面半径缩短到原来的,则圆锥的体积().A.缩小到原来的一半B.扩大到原来的2倍C.不变D.缩小到原来的解析设原圆锥的高为h,底面半径为r,体积为V,则V=r2·h;变化后圆锥的体积V′=×2×2h=πr2·h=V.答案A2.已知水平放置的△ABC“”是按斜二测画法得到如右图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么原△ABC是一个().A.等边三角形B.直角三角形C.三边中有两边相等的等腰三角形D.三边互不相等的三角形解析依据斜二测画法的原则可得,BC=B′C′=2,OA=2×=,∴AB=AC=2,故△ABC是等边三角形.答案A3.顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是().A.16πB.20πC.24πD.32π解析设正四棱柱的底边长为a,球半径为R,则a2·4=16,∴a=2.又(2R)2=22+22+42,∴R2=6.∴S球面=4πR2=4π×6=24π.答案C4.设直线m与平面α相交但不垂直,则下列说法中正确的是().A.在平面α内有且只有一条直线与直线m垂直B.过直线m有且只有一个平面与平面α垂直C.与直线m垂直的直线不可能与平面α平行D.与直线m平行的平面不可能与平面α垂直解析画图或在正方体模型中观察可得.答案B5.如图,α∩β=l,A∈α,B∈α,AB∩l=D,C∈β,C∉l,则平面ABC与平面β的交线是().A.直线ACB.直线ABC.直线CDD.直线BC解析D∈l,l⊂β,∴D∈β.又C∈β,∴CD⊂β.同理CD⊂平面ABC,∴平面ABC∩平面β=CD.答案C6.对两条不相交的空间直线a与b,必存在平面α,使得().A.a⊂α,b⊂αB.a⊂α,b∥αC.a⊥α,b⊥αD.a⊂α,b⊥α解析因为已知两条不相交的空间直线a和b,所以可以在直线a上任取一点A,则A∉b.过A作直线c∥b,则过a,c必存在平面α且使得a⊂α,b∥α.答案B7.已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是().A.AB∥mB.AC⊥mC.AB∥βD.AC⊥β解析容易判断A、B、C三个答案都是正确的,对于D,虽然AC⊥l,但AC不一定在平面α内,故它可以与平面β相交、平行,但不一定垂直.答案D8.如图△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB的大小().A.变大B.变小C.不变D.有时变大有时变小解析由于直线l垂直于平面ABC,∴l⊥BC,又∠ACB=90°,∴AC⊥BC,∴BC⊥平面APC,∴BC⊥PC,即∠PCB为直角,与点P的位置无关,选C.答案C9.设m、n表示不同直线,α、β表示不同平面,则下列结论中正确的是().A.若m∥α,m∥n,则n∥αB.若m⊂α,n⊂β,m∥β,n∥α,则α∥βC.若α∥β,m∥α,m∥n,则n∥βD.若α∥β,m∥α,n∥m,n⊄β,则n∥β解析A选项不正确,n还有可能在平面α内,B选项不正确,平面α还有可能与平面β相交,C选项不正确,n也有可能在平面β内,选项D正确.答案D10.某四面体的三视图如图所示,该四面体四个面的面积中最大的是().A.8B.6C.10D.8解析将三视图还原成几何体的直观图如图所示.它的四个面的面积分别为8,6,10,6,故最大的面积应为10.答案C11.在四面体ABCD中,已知棱AC的长为,其余各棱长都为1,则二面角ACDB的平面角的余弦值为().A.B.C.D.解析取AC的中点E,CD的中点F,连接EF,BF,BE, AC=,其余各棱长都为1,∴AD⊥CD.∴EF⊥CD.又 BF⊥CD,∴∠BFE是二面角ACDB的平面角. EF=,BE=,BF=,∴EF2+BE2=BF2.∴∠BEF=90°,∴cos∠BFE==.答案C12.如图所示,在正方体ABCDA1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与直线A1D1,EF,CD都相交的直线().A.不存在B.有且只有两条C.有且只有三条D.有无数条解析在EF上任意取一点M,直线A1D1与M确定一个平面,这个平面与CD有且仅有1个交点N,当M取不同的位置就确定不同的平面,从而与CD有不同的交点N,而直线MN与这3条异面直线都有交点,如下图,故选D.答案D二、填空题(本大题共4小题,每小题5分,共...