牛顿科特斯公式的特点总结VIP免费

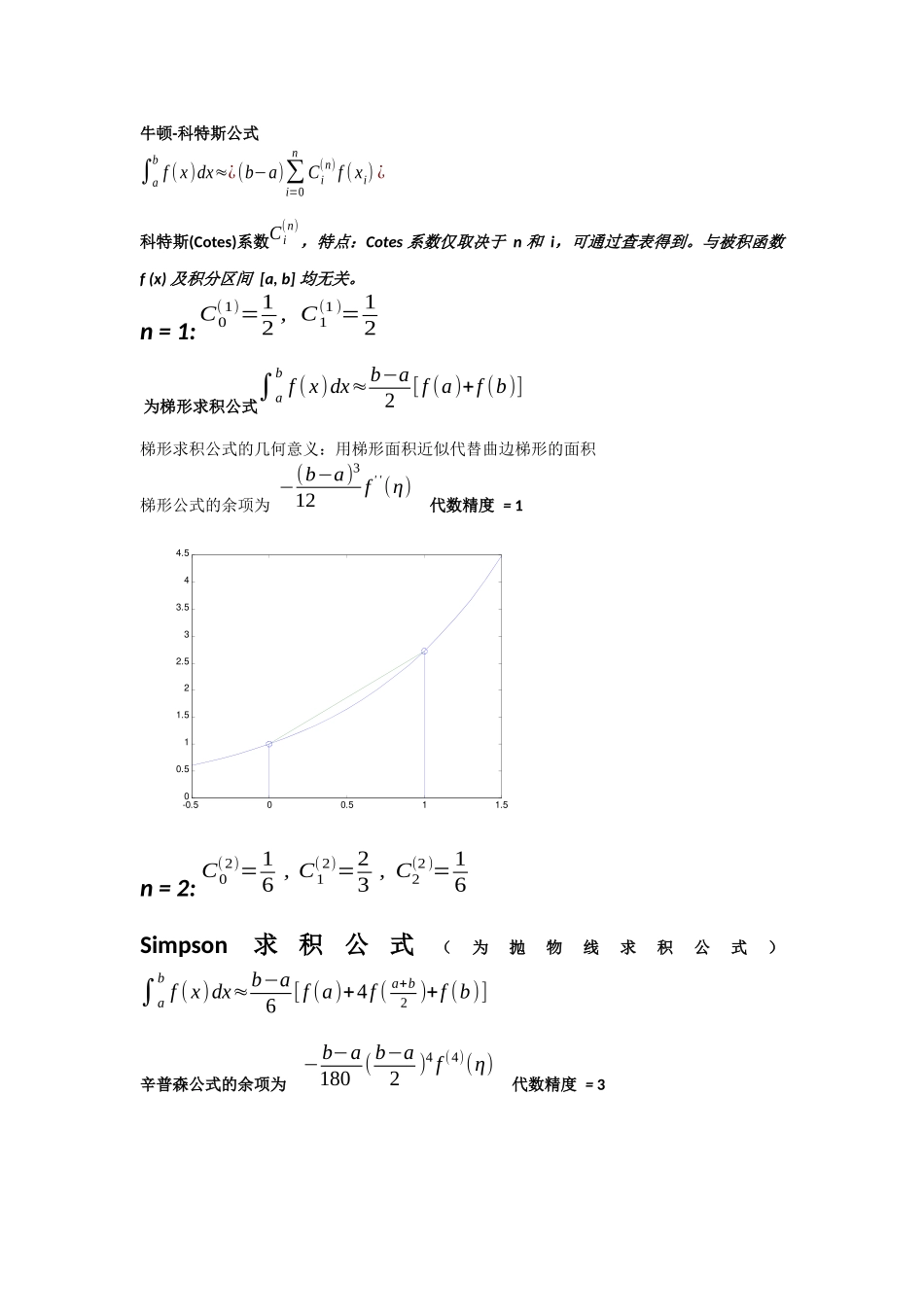
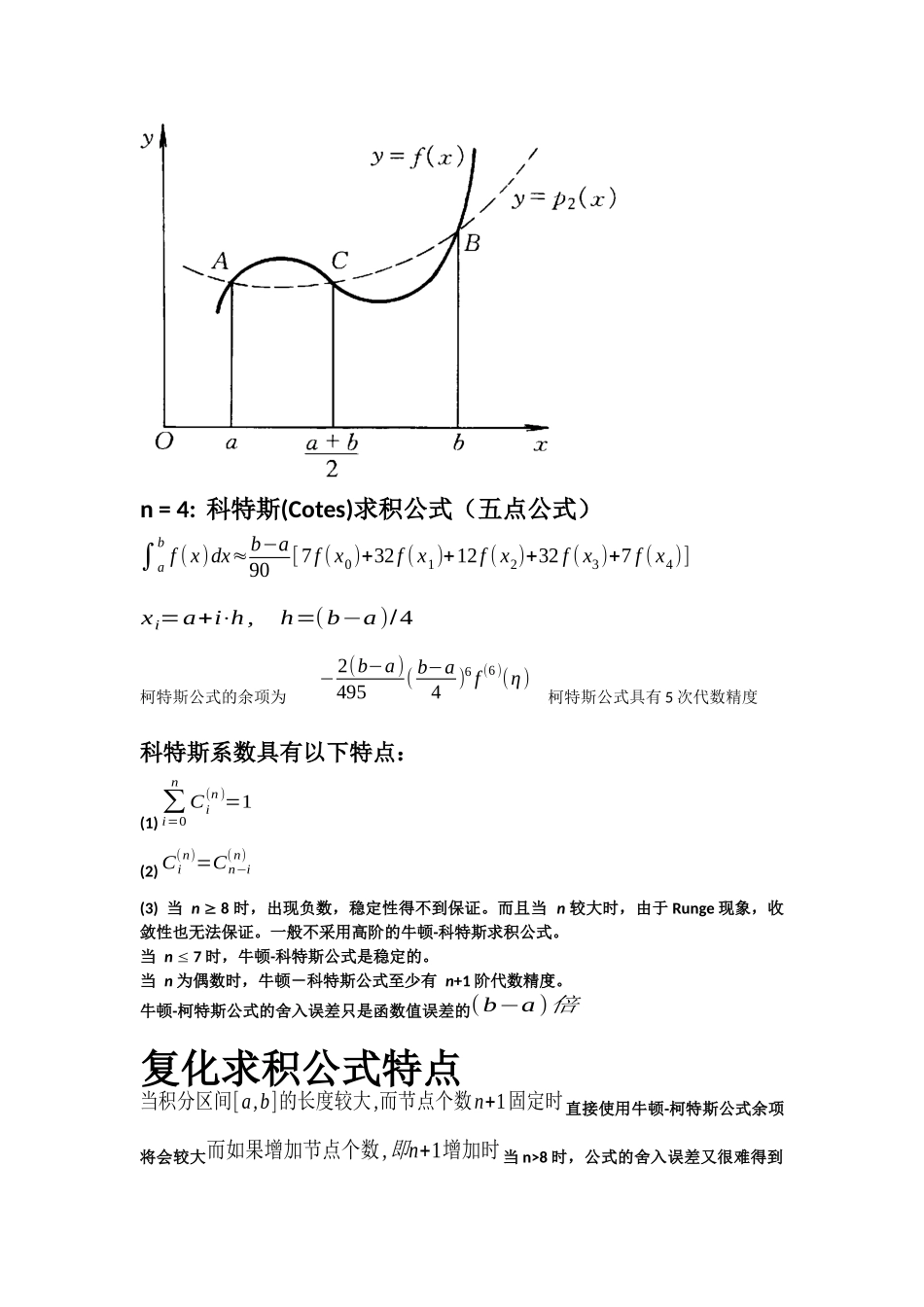
牛顿-科特斯公式∫abf(x)dx≈¿(b−a)∑i=0nCi(n)f(xi)¿科特斯(Cotes)系数Ci(n)，特点：Cotes系数仅取决于n和i，可通过查表得到。与被积函数f(x)及积分区间[a,b]均无关。n=1:C0(1)=12,C1(1)=12为梯形求积公式∫abf(x)dx≈b−a2[f(a)+f(b)]梯形求积公式的几何意义：用梯形面积近似代替曲边梯形的面积梯形公式的余项为−(b−a)312f''(η)代数精度=1-0.500.511.500.511.522.533.544.5n=2:C0(2)=16,C1(2)=23,C2(2)=16Simpson求积公式（为抛物线求积公式）∫abf(x)dx≈b−a6[f(a)+4f(a+b2)+f(b)]辛普森公式的余项为−b−a180(b−a2)4f(4)(η)代数精度=3n=4:科特斯(Cotes)求积公式（五点公式）∫abf(x)dx≈b−a90[7f(x0)+32f(x1)+12f(x2)+32f(x3)+7f(x4)]xi=a+i⋅h,h=(b−a)/4柯特斯公式的余项为−2(b−a)495(b−a4)6f(6)(η)柯特斯公式具有5次代数精度科特斯系数具有以下特点：(1)∑i=0nCi(n)=1(2)Ci(n)=Cn−i(n)(3)当n8时，出现负数，稳定性得不到保证。而且当n较大时，由于Runge现象，收敛性也无法保证。一般不采用高阶的牛顿-科特斯求积公式。当n7时，牛顿-科特斯公式是稳定的。当n为偶数时，牛顿－科特斯公式至少有n+1阶代数精度。牛顿-柯特斯公式的舍入误差只是函数值误差的(b−a)倍复化求积公式特点当积分区间[a,b]的长度较大,而节点个数n+1固定时直接使用牛顿-柯特斯公式余项将会较大而如果增加节点个数,n即+1增加时当n>8时，公式的舍入误差又很难得到控制此时，使用复化方法，即将积分区间[a,b]分成若干个子区间然后在每个小区间上使用低阶牛顿-柯特斯公式，最后将每个小区间上的积分的近似值相加，这种方法称为复化求积法复化梯形求积公式∫abf(x)dx≈Tn=h2[f(a)+2∑k=1n−1f(xk)+f(b)]复化梯形公式余项为−(b−a)12h2f''(η)误差是h2阶limn→∞h→0Tn=∫abf(x)dx即复化梯形公式是收敛的复化辛普森求积公式∫abf(x)dx≈Sn=h6[f(a)+4∑k=0n−1f(xk+12)+2∑k=1n−1f(xk)+f(b)]n则足够大时,复合Simpson公式的余项为Rn(f)=I−Sn=−b−a180(h2)4f(4)(η),¿η∈(a,b)¿误差是h4阶，limn→∞h→0Sn=∫abf(x)dx复化辛普森公式是收敛的复化柯特斯求积公式∫abf(x)dx≈Cn=b−a90n[7f(a)+∑k=0n−1[32f(xk+14)+12f(xk+24)+32f(xk+34)]+14∑k=1n−1f(xk)+7f(b)]f若(x)∈C6[a,b],同样可得复合Cotes公式的余项I−Cn=−2(b−a)945(h4)6f(6)(η)n→∞时，复化柯特斯公式也是收敛的],[ba三种复化公式的的余项I−Tn=∑k=0n−h12⋅h2⋅f''(ηk)=O(h2)I−Sn=∑k=0n−h180(h2)4f(4)(ηk)=O(h4)I−Cn=∑k=0n−2h945(h4)6f(6)(ηk)=O(h6)分别是h的2，4，6阶无穷小量T即n,Sn,Cn趋于定积分I的速度依次更快