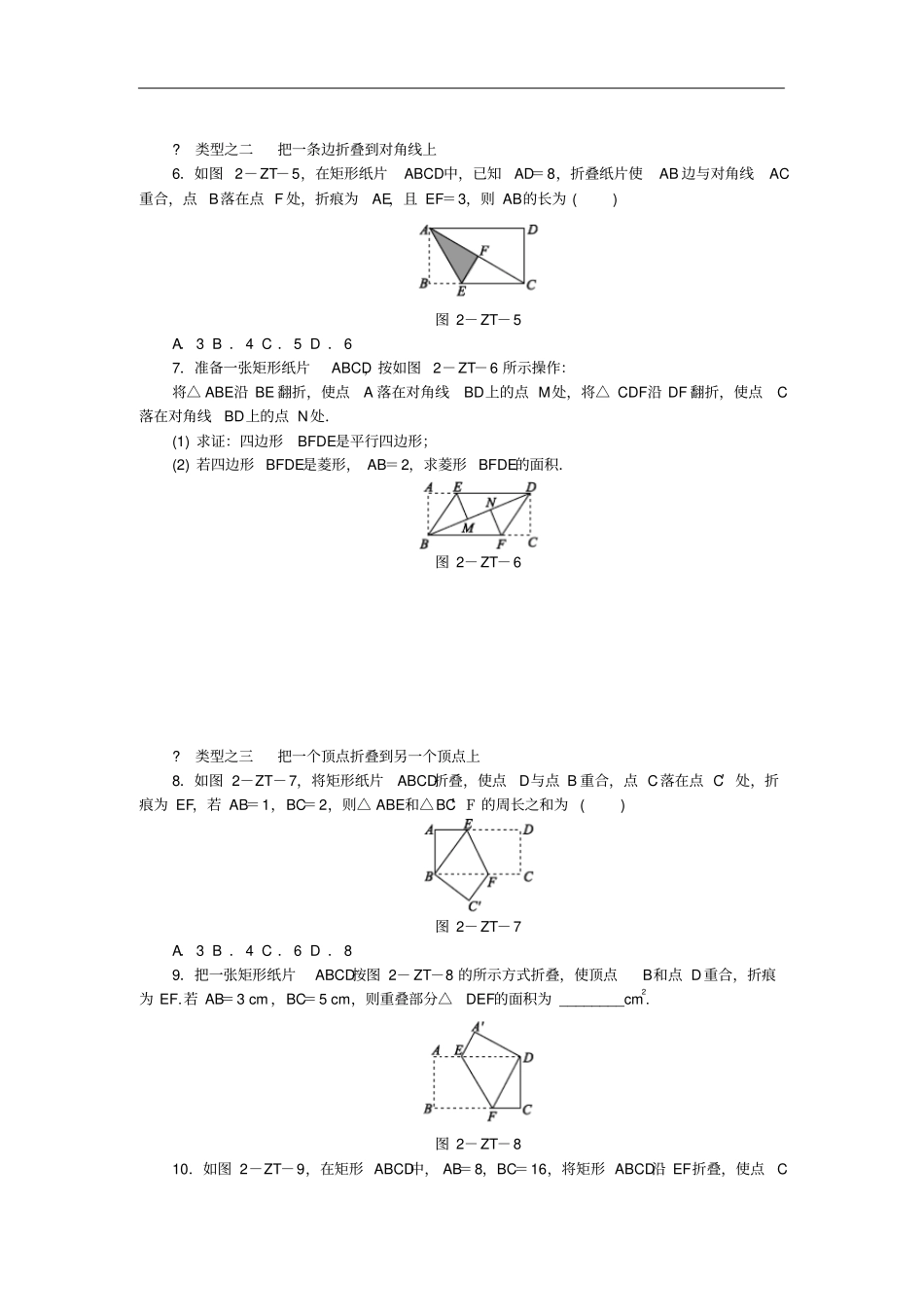
专题训练(二)特殊平行四边形中的折叠问题?类型之一把一个顶点折叠到一条边上1.2017·天水如图2-ZT-1,在矩形ABCD中,∠DAC=65°,E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=________°.图2-ZT-12.如图2-ZT-2,将矩形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为________.图2-ZT-23.如图2-ZT-3,在矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC上的点F处.若AE=5,BF=3,求CD的长.图2-ZT-34.某校八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处.请你根据①②步骤计算EC的长.5.如图2-ZT-4,已知矩形纸片ABCD,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.求证:A,G,E,F四点构成的四边形是菱形.图2-ZT-4?类型之二把一条边折叠到对角线上6.如图2-ZT-5,在矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为()图2-ZT-5A.3B.4C.5D.67.准备一张矩形纸片ABCD,按如图2-ZT-6所示操作:将△ABE沿BE翻折,使点A落在对角线BD上的点M处,将△CDF沿DF翻折,使点C落在对角线BD上的点N处.(1)求证:四边形BFDE是平行四边形;(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.图2-ZT-6?类型之三把一个顶点折叠到另一个顶点上8.如图2-ZT-7,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为()图2-ZT-7A.3B.4C.6D.89.把一张矩形纸片ABCD按图2-ZT-8的所示方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积为________cm2.图2-ZT-810.如图2-ZT-9,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,求折痕EF的长.图2-ZT-9?类型之四沿一条直线折叠11.如图2-ZT-10,已知正方形ABCD的对角线长为22,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为()图2-ZT-10A.82B.42C.8D.612.如图2-ZT-11,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在的直线折叠得到△EB′F,连接B′D,则B′D的最小值是()图2-ZT-11A.210-2B.6C.213-2D.413.2017·宁夏如图2-ZT-12,将平行四边形ABCD沿对角线BD折叠,使点A落在点A′处.若∠1=∠2=50°,则∠A′的度数为________.图2-ZT-1214.2017·西宁如图2-ZT-13,将平行四边形ABCD沿EF对折,使点A落在点C处.若∠A=60°,AD=4,AB=6,则AE的长为________.图2-ZT-1315.如图2-ZT-14,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使点B落在点P处,折痕为EC,连接AP并延长交CD于点F,连接BP.(1)求证:四边形AECF为平行四边形;(2)若△AEP是等边三角形,求证:△APB≌△EPC;(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.图2-ZT-14详解详析1.[答案]402.[答案]12[解析]由折叠的性质知,AF=AB,EF=BE.所以矩形的周长等于△AFD和△CFE的周长的和.故矩形ABCD的周长为12.3.解:根据折叠的性质,得EF=AE=5.根据矩形的性质,得∠B=90°.在Rt△BEF中,∠B=90°,EF=5,BF=3,根据勾股定理,得BE=EF2-BF2=52-32=4,∴CD=AB=AE+BE=5+4=9.4.解:设EC=xcm,则EF=DE=(16-x)cm.由题意得AF=AD=20cm.在Rt△ABF中,BF=AF2-AB2=12cm,FC=BC-BF=20-12=8(cm).在Rt△EFC中,EF2=FC2+EC2,即(16-x)2=82+x2,解得x=6,∴EC的长为6cm.5.证明:连接AF.由折叠的性质,得AG=EG,∠AGF=∠EGF. DC∥AB,∴∠EFG=∠AGF,∴∠EFG=∠EGF,∴EF=EG.又 AG=EG,∴EF=AG,∴四边形AGEF是平行四边形.又 AG=EG,∴平行四边形AGEF是菱形,即A,G,E,F四点构成的四边形是菱形.6.D7...