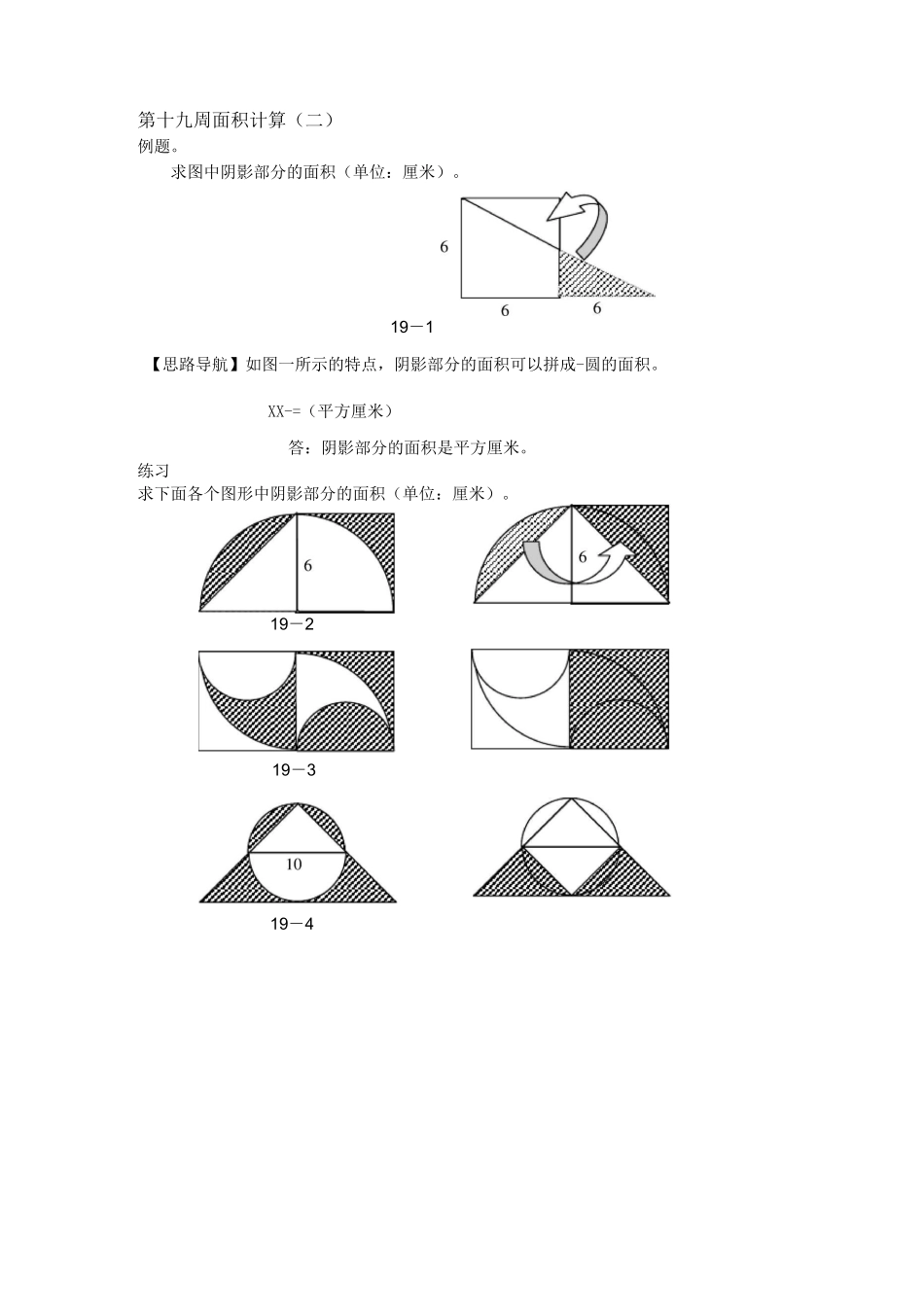
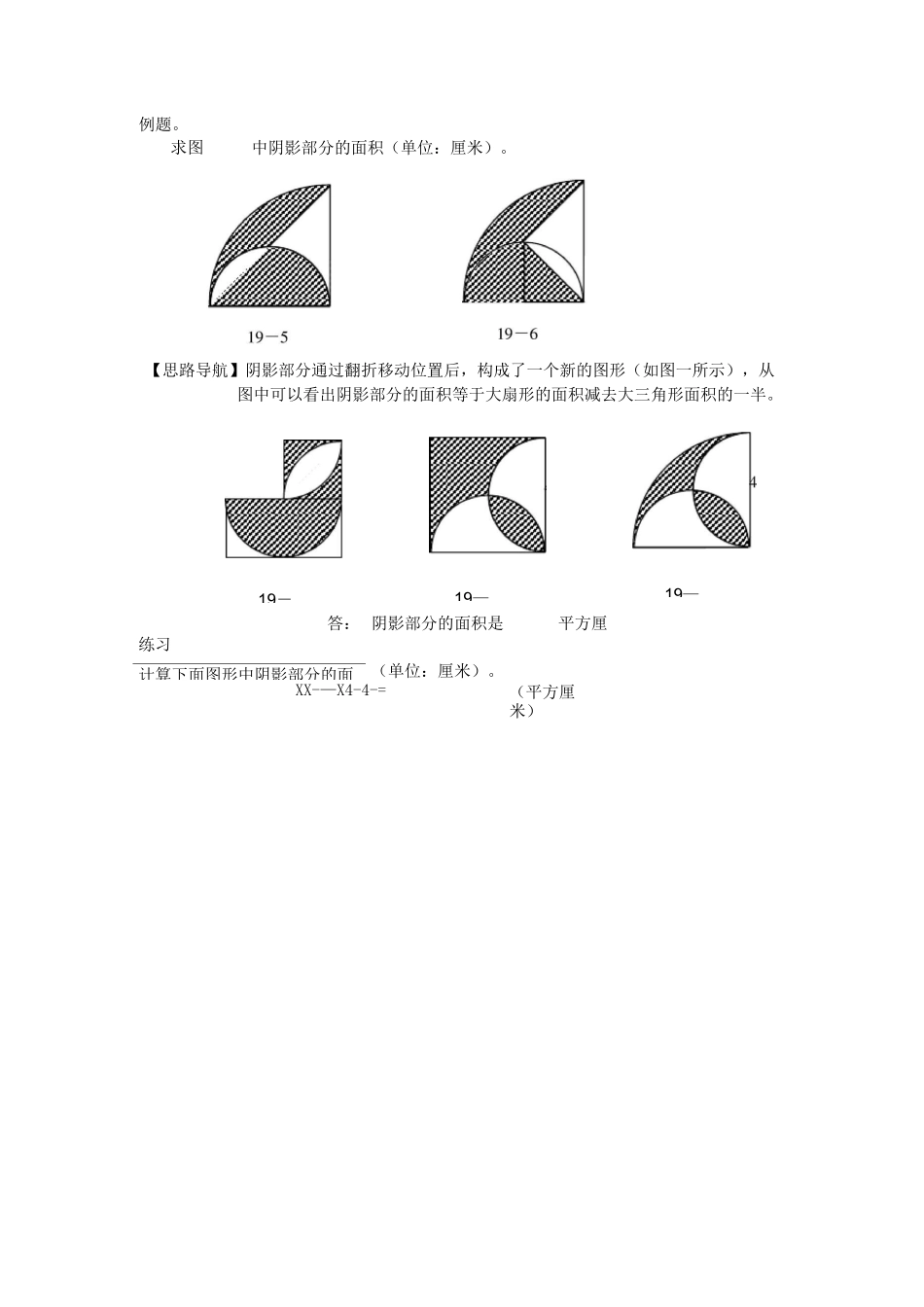
第十九周面积计算(二)例题。求图中阴影部分的面积(单位:厘米)。19-1【思路导航】如图一所示的特点,阴影部分的面积可以拼成-圆的面积。XX-=(平方厘米)答:阴影部分的面积是平方厘米。练习求下面各个图形中阴影部分的面积(单位:厘米)。19-219-319-419-19—19—【思路导航】阴影部分通过翻折移动位置后,构成了一个新的图形(如图一所示),从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。答:阴影部分的面积是平方厘米。练习(单位:厘米)。计算下面图形中阴影部分的面例题。求图中阴影部分的面积(单位:厘米)。XX-—X4-4-=(平方厘米)例题。如图一所示,两圆半径都是厘米,且图中两个阴影部分的面积相等。求长方形的面积。思路导航】因为两圆的半径相等,所以两个扇形中的空白部分相等。又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半(如图一右图所示)。所以XX-X=(平方厘米)答:长方形长方形的面积是平方厘米。练习、如图一所示,圆的周长为厘米,两点把圆分成相等的两段弧,阴影部如所厘米,求阴影部分的面如所示,分()的面积与阴影部分()的面积相等,求平行四边形CCB19-1519-1619-17例题。如所示,求阴影部分的面积(单位:厘AE419-14【思路导航】我们可以把三角形看成是长方形的一部分,把它还原成长方形后(如右图所示),因为原大三角形的面积与后加上的三角形面积相等,并且空白部分的两组三角形面积分别相等,所以和的面积相等。X=(平方厘米)答:阴影部分的面积是平方厘米。练习、如图一所示,求四边形的面积。如图一所示,长厘米,长方形面积是平方厘米。求的长度。图一是两个完全一样的直角三角形重叠在一起,按照图中的已知条件求阴影部分的面积(单位:厘米)。CC6DC2、如图3、如例题。如图一所示,图中圆的直径是厘米,平行四边形的面积是平方厘米,Z=度,求阴影部分的面积(得数保留两位小数)。【思路导航】阴影部分的面积等于平行四边形的面积减去扇形的面积,再减去三角形的面积。半径:三=(厘米)扇形的圆心角:一(一x)=(度)扇形的面积:xxx——*(平方厘米)三角形的面积:三三=(平方厘米)—()=(平方厘米)答:阴影部分的面积是平方厘米。练习1、如图一所示,Z=度,圆的周长位厘米,平行四边形的面积为平方厘米。求阴影部分的面积(得数保留两位小数)。所示,三角形的面积是平方厘米,圆的直径=厘米,。求阴影部分的面积。所示,求阴影部分的面积(单位:厘米。得数保留两位小数)。BB第周答案:练1、图答一阴影部分的面积为:Xx-=平方厘米2、图答一阴影部分的面积为:X=平方厘米3、图答一阴影部分的面积为:X(-b)X-X=平方厘米练、图答一中阴影部分的面积为:()X=平方厘米、图答一阴影部分的面积为:XX-=平方厘米、图答一阴影部分的面积为:XX--XX-=平方厘米练、图答一中,阴影部分()的面积与阴影部分()的面积相等。所以,平行四边形的面积和圆的面积相等。因此,平行四边形的面积是:(三三)X=平方厘米、(三)XX-=平方厘米、(三)XX-(三)X—=平方厘米第二题和第三题,阴影部分的面积通过等积变形后可知。如图答一和图答—所示。练、如图答一所示:延长和相距与,四边形的面积是:XX-—XX-=平方厘米、如图答一所示,因为=,所以=三=厘米、如图答一所示:阴影部分面积等于梯形的面积,其面积为:(一)X三=平方厘米练、如图答一所示圆心角的度数为一(一X)=度平行四边形内一个小弓形的面积为(三-4-)XX———-4-=平方厘米阴影部分的面积为4—=平方厘米、如图答一所示:圆心角的度数为一(一X)=度扇形的面积为(4)XX——=平方厘米阴影部分的面积为一如图答一()所示:X_=平方厘米圆心角的度数为一X=度扇形的面积(三)XX—平方厘米三角形的面积为(-4-)XX-=平方厘米阴影部分的面积一=平方厘米如图答—()所示圆心角的读书一(一X)=度扇形的面积XX=平方厘米三角形的面积()XX-=平方厘米扇形的面积(三)XX—平方厘米阴影部分的面积一一=平方厘米