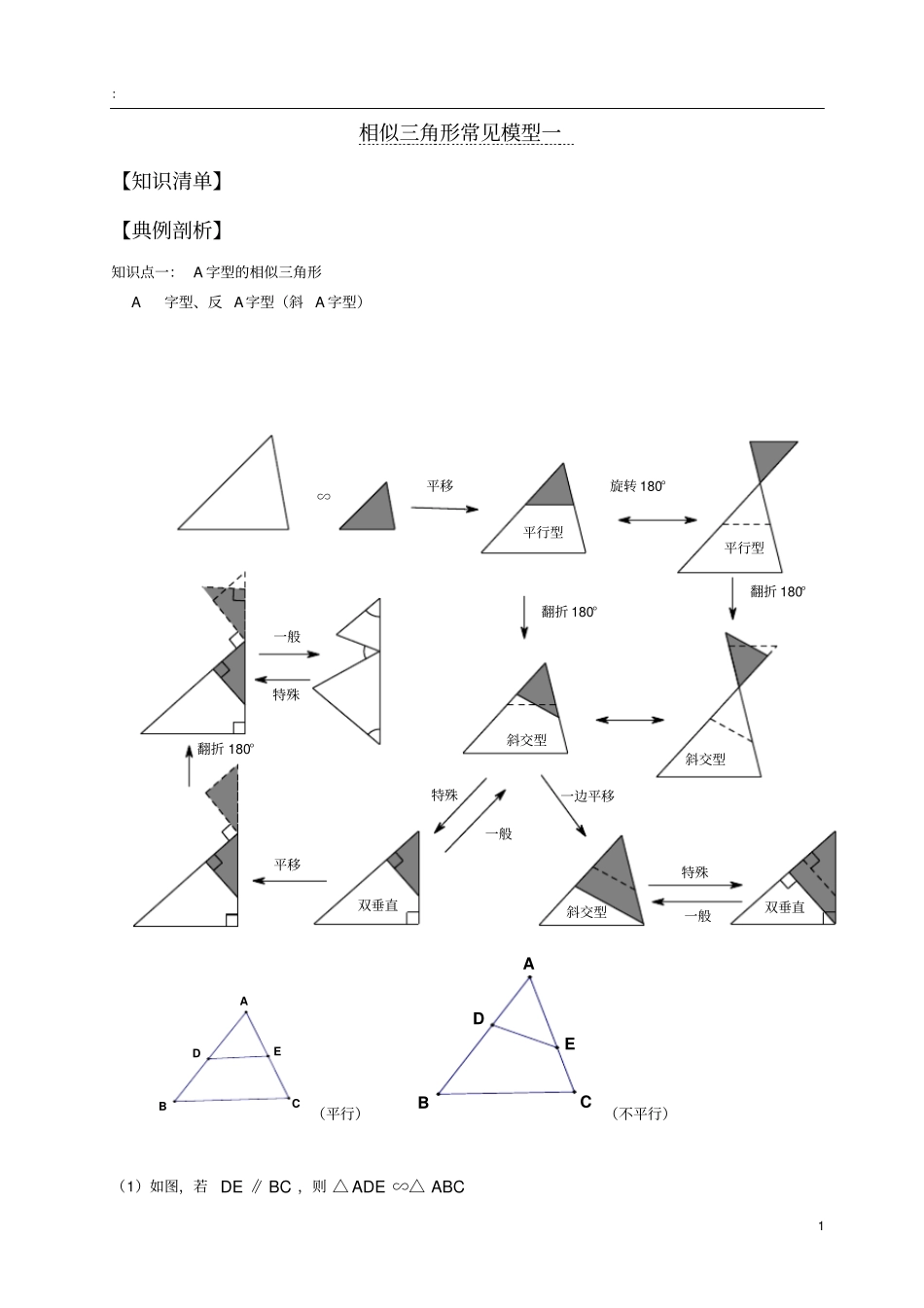
:1相似三角形常见模型一【知识清单】【典例剖析】知识点一:A字型的相似三角形A字型、反A字型(斜A字型)ABCDE(平行)CBADE(不平行)(1)如图,若BCDE∥,则ABCADE∽△△特殊一般翻折180°平移特殊一般一般翻折180°双垂直双垂直斜交型斜交型斜交型平行型平行型特殊一边平移翻折180°旋转180°平移∽:2(2)如图,如果BAED,或CADE,则ACBADE∽△△1、如图,已知////ABEFCD,若ABa,CDb,EFc,求证:111cab.2、已知在ABC△中,D是AB上的点,E是AC上的点,连接DE,可得180CBDE,线段BCDE21,AEAD32,求ACAB的值。变式练习:1、如图,111EEFFMM∥∥,若AEEFFMMB,则111111:::_________AEEEEFFFFMMMMCBSSSS四边形四边形四边形2、如图,ADEFMNB∥∥∥,若9AD,18BC,::2:3:4AEEMMB,则_____EF,_____MN3、(2014?乌鲁木齐)如图,AD∥BC,∠D=90°,AD=2,BC=5,DC=8.若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有()A、1个B、2个C、3个D、4个知识点二:8字型相似三角形FEDCBACBADEM1F1E1MEFABCMNABCDEF:3JOADBCABCD(蝴蝶型)(平行)(不平行)(1)如图,若CDAB∥,则DOCAOB∽△△(2)如图,若CA,则CDJABJ∽△△1、已知,P为平行四边形ABCD对角线,AC上一点,过点P的直线与AD,BC,CD的延长线,AB的延长线分别相交于点E,F,G,H求证:PEPHPFPG2、如图,设ABBCCAADDEEA,求证:12变式练习:1、(2010?威海)如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1.PHGFEDCBA21ABCDE:4﹙1﹚将△ABC,△A1B1C1如图②摆放,使点A1与B重合,点B1在AC边的延长线上,连接CC1交BB1于点E.求证:∠B1C1C=∠B1BC.﹙2﹚若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F,试判断∠A1C1C与∠A1BC是否相等,并说明理由.﹙3﹚写出问题﹙2﹚中与△A1FC相似的三角形.2、如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点。(1)若BK=52KC,求CDAB的值;:5ABCDEK(2)连接BE,若BE平分∠ABC,则当AE=12AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.再探究:当AE=1nAD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.知识点三:母子型证明三角形相似ABCDCAD(1)如图,若BACD,则ABCACD∽△△(2)如图,若BCAC,ABCD,则ACBCDBADC∽△∽△△如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E.B:6求证:OEOAOC2.变式练习:1、已知:在正三角形ABC中,点D、E分别是AB、BC延长线上的点,且BDCE,直线CD与AE相交于点F求证:①DCAE,②2ADDCDF2、已知:如图,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:EGEFBE2.【课后练习】ABCDEF:71、已知:在ABC中,D为AB中点,E为AC上一点,且2AEEC,BE、CD相交于点F,求BFEF的值3、已知:如图,在Rt△ABC中,∠C=90°,BC=2,AC=4,P是斜边AB上的一个动点,PD⊥AB,交边AC于点D(点D与点A、C都不重合),E是射线DC上一点,且∠EPD=∠A.设A、P两点的距离为x,△BEP的面积为y.(1)求证:AE=2PE;(2)求y关于x的函数解析式,并写出它的定义域;(3)当△BEP与△ABC相似时,求△BEP的面积.FEDCBAACBPDE(第3题图)