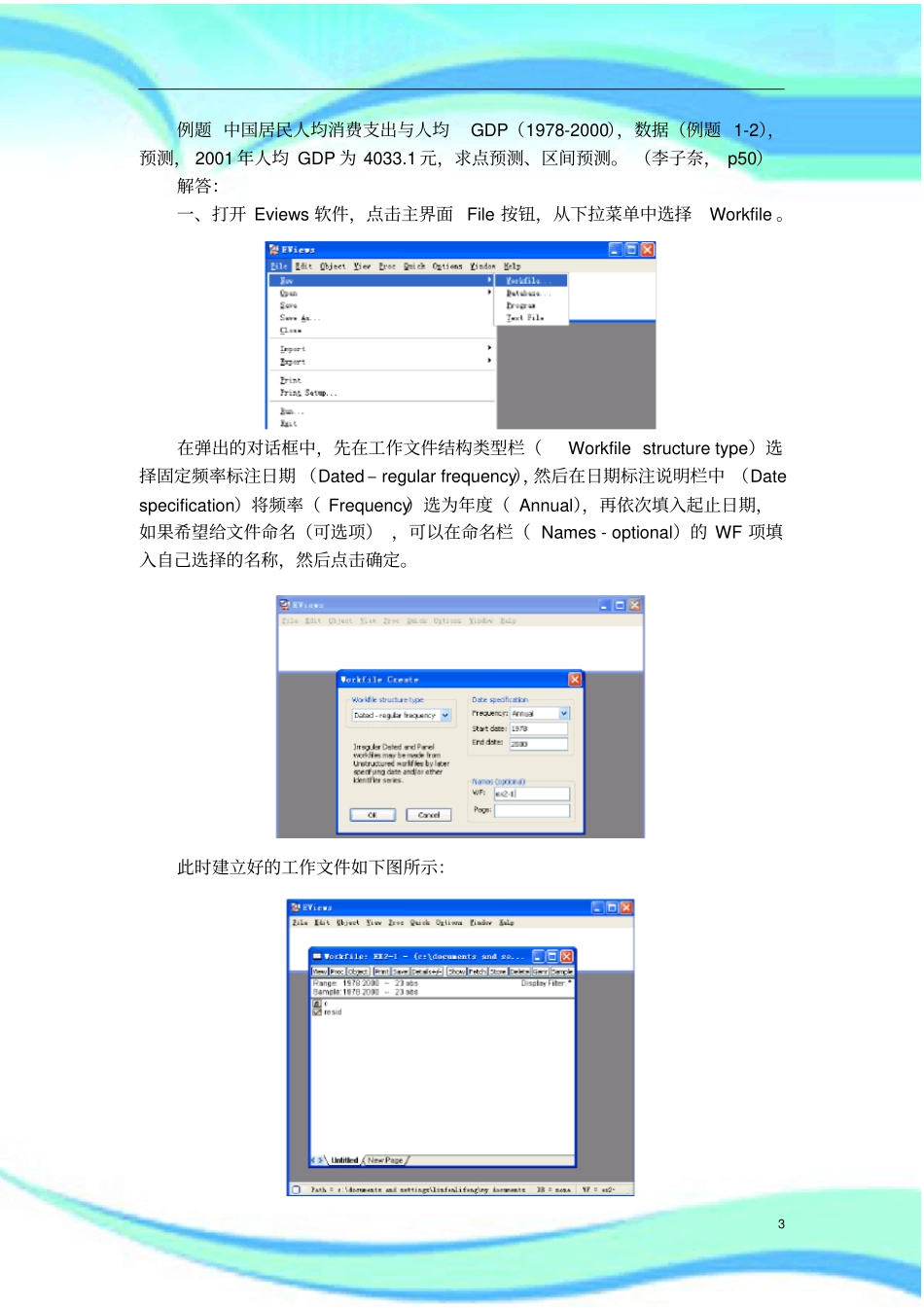
利用Eviews软件进行最小二乘法回归实例2————————————————————————————————作者:————————————————————————————————日期:3例题中国居民人均消费支出与人均GDP(1978-2000),数据(例题1-2),预测,2001年人均GDP为4033.1元,求点预测、区间预测。(李子奈,p50)解答:一、打开Eviews软件,点击主界面File按钮,从下拉菜单中选择Workfile。在弹出的对话框中,先在工作文件结构类型栏(Workfilestructuretype)选择固定频率标注日期(Dated–regularfrequency),然后在日期标注说明栏中(Datespecification)将频率(Frequency)选为年度(Annual),再依次填入起止日期,如果希望给文件命名(可选项),可以在命名栏(Names-optional)的WF项填入自己选择的名称,然后点击确定。此时建立好的工作文件如下图所示:4在主界面点击快捷方式(Quick)按钮,从下拉菜单中选空白数据组(EmptyGroup)选项。此时空白数据组出现,可以在其中通过键盘输入数据或者将数据粘贴过来。在Excel文件(例题1-2)中选定要粘贴的数据,然后在主界面中点击编辑(Edit)按钮,从下拉菜单中选择粘贴(Paste),数据将被导入Eviews软件。5将右侧的滚动条拖至最上方,可以在最上方的单元格中给变量命名。二、估计参数在主界面中点击快捷方式(Quick)按钮,从下拉菜单中选择估计方程(EstimateEquation)在弹出的对话框中设定回归方程的形式。6在方程表示式栏中(Equationspecification),按照被解释变量(Consp)、常数项(c)、解释变量(Gdpp)的顺序填入变量名,在估计设置(Estimationsettings)栏中选择估计方法(Method)为最小二乘法(LS–LeastSquares),样本(Sample)栏中选择全部样本(本例中即为1978-2000),然后点击确定,即可得到回归结果。以上得到的回归结果可以表示为:·201.1190.3862(13.51)(53.47)ConspGDPP如果你试图关闭回归方程页面(或Eviews主程序),这时将会弹出一个对话框,询问是否删除未命名的回归方程,如下图所示7此时如果同意删除,可以点击Yes,如果想把回归结果保存下来,可以点击命名(Name),这时就会弹出一个对话框,在其中填入为方程取的名字,点击OK即可。本例中方程自动命名为方程-1(eq01)。点击确定之后,方程页面关闭,同时在工作文件页面内可以发现多了一个表示回归方程的对象(图中的eq01)。如果以后需要用到回归结果时,就不需要象前面那样逐步地去做,而只需要双击eq01图标即可。如果试图关闭工作文件或Eviews主程序,将会弹出警示框询问是否对该工作文件进行保存,此时如果不计划对工作文件进行保存,直接点击No即可,如果点击取消(Cancel),将回到关闭前的状态。如果计划保存工作文件以备将来使用,则可以点击Yes。8随后弹出的对话框询问按照怎样的精确度保存数据,此时选择高精确度即可。即选择Doubleprecision。注意!按照当前的设置,Eviews默认的保存路径是“我的文档”。将来打开文件时可以从Eviews主程序中按照文件(File)——打开(Open)——Eviews工作文件(EviewsWorkfile)的方式,也可以直接在“我的文档”中双击要打开的工作文件。三、相关的检验1.拟合优度(可决系数)从回归结果中可以看出,本例中20.9927R,说明模型在整体上拟合得非常好。2.显著性检验首先看截距项和斜率项的t统计量取值情况。因为本例中使用的观察值个数为23,因此这些t统计量应该服从自由度为(232)21的t分布,查书后附录中给出的t分布表,可以发现自由度为21、检验水平为0.1、0.05、0.01时相对应的临界值分别为1.721、2.080、2.831,而本例中的两个t统计量的取值分别为13.51和53.47,说明在通常使用的检验水平下,本例中所选择的两个解释变量对被解释变量有很好的解释能力,或者说数据强烈支持将这两个解释变量纳入模型之中。3.置信区间以下建立总体参数0和1置信度为95%的置信区间。前面已经介绍过,当置信度为1时,置信区间为2211??11??(2),(2)ttnsns而0.025(21)2.080t,从回归结果中还可以查到1?0.007222s,因此1的置信度为95%的置信区间为0.38622.0800.0072220.38620.0150。或者...