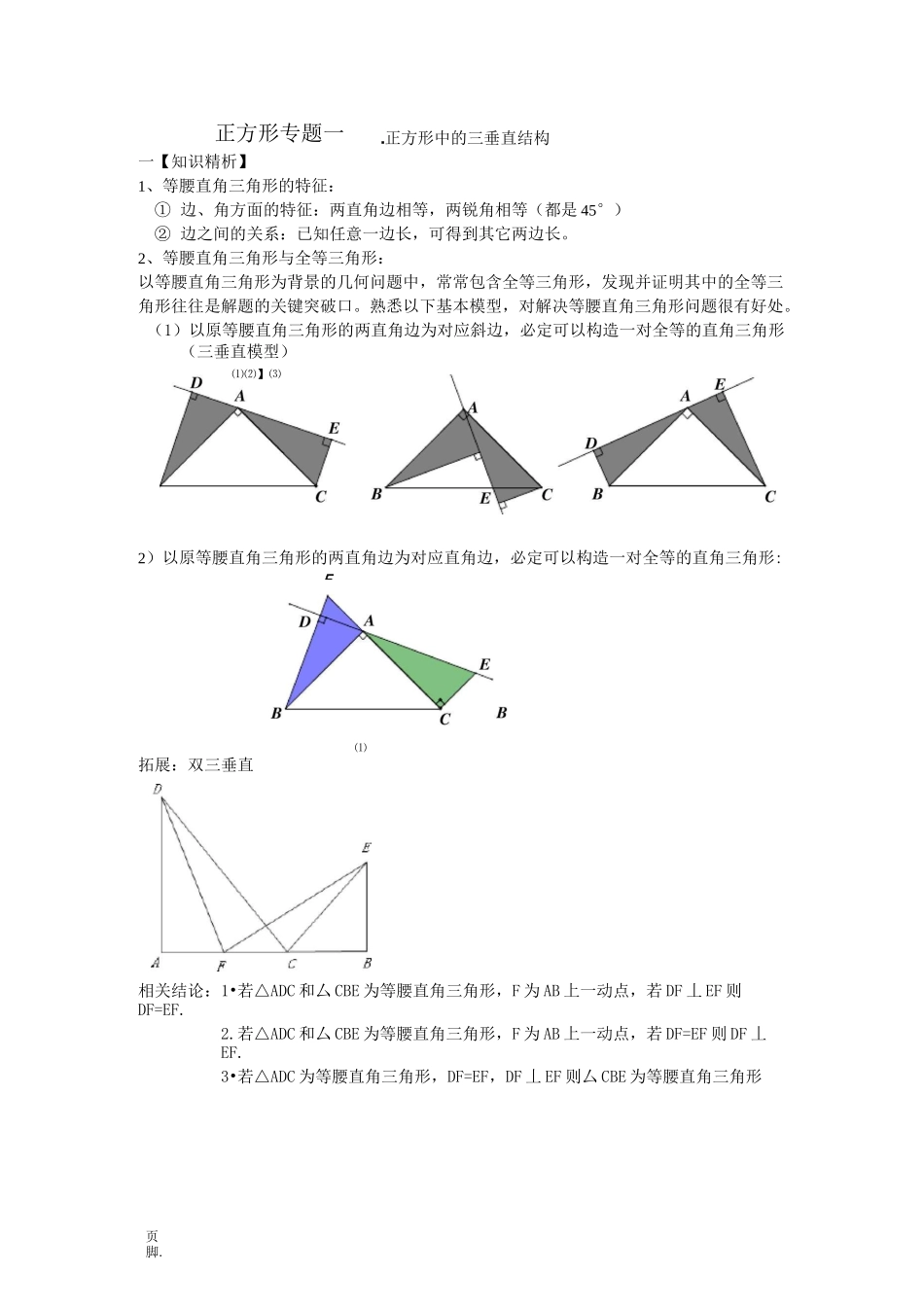
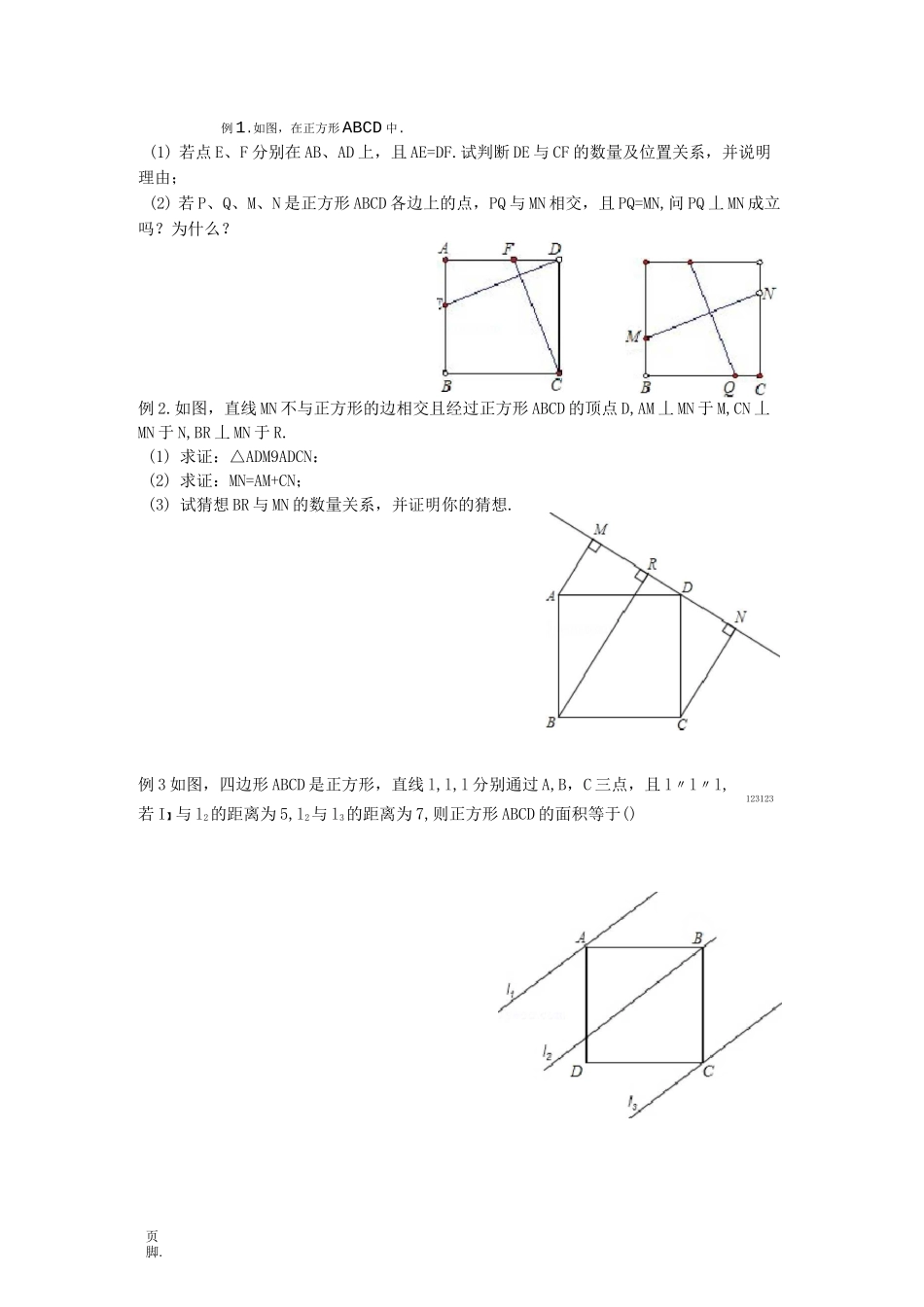
页脚.一【知识精析】1、等腰直角三角形的特征:①边、角方面的特征:两直角边相等,两锐角相等(都是45°)②边之间的关系:已知任意一边长,可得到其它两边长。2、等腰直角三角形与全等三角形:以等腰直角三角形为背景的几何问题中,常常包含全等三角形,发现并证明其中的全等三角形往往是解题的关键突破口。熟悉以下基本模型,对解决等腰直角三角形问题很有好处。(1)以原等腰直角三角形的两直角边为对应斜边,必定可以构造一对全等的直角三角形(三垂直模型)2)以原等腰直角三角形的两直角边为对应直角边,必定可以构造一对全等的直角三角形:拓展:双三垂直相关结论:1•若△ADC和厶CBE为等腰直角三角形,F为AB上一动点,若DF丄EF则DF=EF.2.若△ADC和厶CBE为等腰直角三角形,F为AB上一动点,若DF=EF则DF丄EF.3•若△ADC为等腰直角三角形,DF=EF,DF丄EF则厶CBE为等腰直角三角形⑴⑵】⑶正方形专题一F■正方形中的三垂直结构⑴页脚.例1.如图,在正方形ABCD中.(1)若点E、F分别在AB、AD上,且AE=DF.试判断DE与CF的数量及位置关系,并说明理由;(2)若P、Q、M、N是正方形ABCD各边上的点,PQ与MN相交,且PQ=MN,问PQ丄MN成立吗?为什么?例2.如图,直线MN不与正方形的边相交且经过正方形ABCD的顶点D,AM丄MN于M,CN丄MN于N,BR丄MN于R.(1)求证:△ADM9ADCN:(2)求证:MN=AM+CN;(3)试猜想BR与MN的数量关系,并证明你的猜想.例3如图,四边形ABCD是正方形,直线l,l,l分别通过A,B,C三点,且l〃l〃l,123123若I】与l2的距离为5,l2与l3的距离为7,则正方形ABCD的面积等于()例5如图,直线AB交x轴正半轴于点页脚.例4.如图在平面直角坐标系中正方形OABC的边OC,OA分别在x轴正半轴上和y轴的负半轴上,点B(a,b)在第四象限且满足b=-2+\;2-a-2.(1)求点B的坐标;(2),E,F为OC,OA上的动点,连接BE,CF交于M点,满足ZOEF=45°,是否存在点E,F,使得BE丄CF?若存在,求出E,F的坐标;若不存在,请说明理由;(3)F在线段0A上,连BF,作0M丄BF于M,AN丄BF于N,当F在线段0A上运动时(不与O、A重合),■的值是否变化•若变化,求出变化的围;若不变,求其值.满足2一4+|4—b|=0(1)求A、B两点的坐标;(2)D为0A的中点,连接BD,过点0作0E丄BD于F,交AB于E,求证ZBDO=ZEDA;(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰RtAPBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段0Q的长是否发生变化?若不变,求其值;若变化,求线段0Q的取值围.且a、b页脚.例题6、1、如图,在正方形ABCD中,E是AD的中点,BD与CE交于F点,求证:AF丄BE。2、已知正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN丄DM且交ZCBE的平分线于N。(1)求证:MD=MN;(2)若将上述条件中的“M是AB的中点”改为“M是AB上任意一点”,其余条件不变,则结论“MD=MN”还成立吗?如果成立,请证明;如果不成立,请说明理由。例7、如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.例8.如图1,四边形ABCD为正方形,E在CD上,ZDAE的平分线交CD于F,BG丄AF于G,交AE于H.(1)如图1,ZDEA=60°,求证:AH=DF;(2)如图2,E是线段CD上(不与C、D重合)任一点,请问:AH与DF有何数量关系并证明你的结论;(3)如图3,E是线段DC延长线上一点,若F是厶ADE中与ZDAE相邻的外角平分线与CD的交点,其它条件不变,请判断AH与DF的数量关系(画图,直接写出结论,不需证明).BC第1题图第2题图第2题图页脚.例9.操作,将一把含45°的直三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑行,直角的一边始终经过点B,另一边与射线DC相交于点Q。探究:设A、P两点间的距离为x。(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的关系?试证明你观察得到的结论;(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系式。(3)当点P在线段AC上滑行时,APCQ是否可能成为等腰三角形,如果可能,指出所有能使APCQ成为等腰三角形的点Q的位置,...