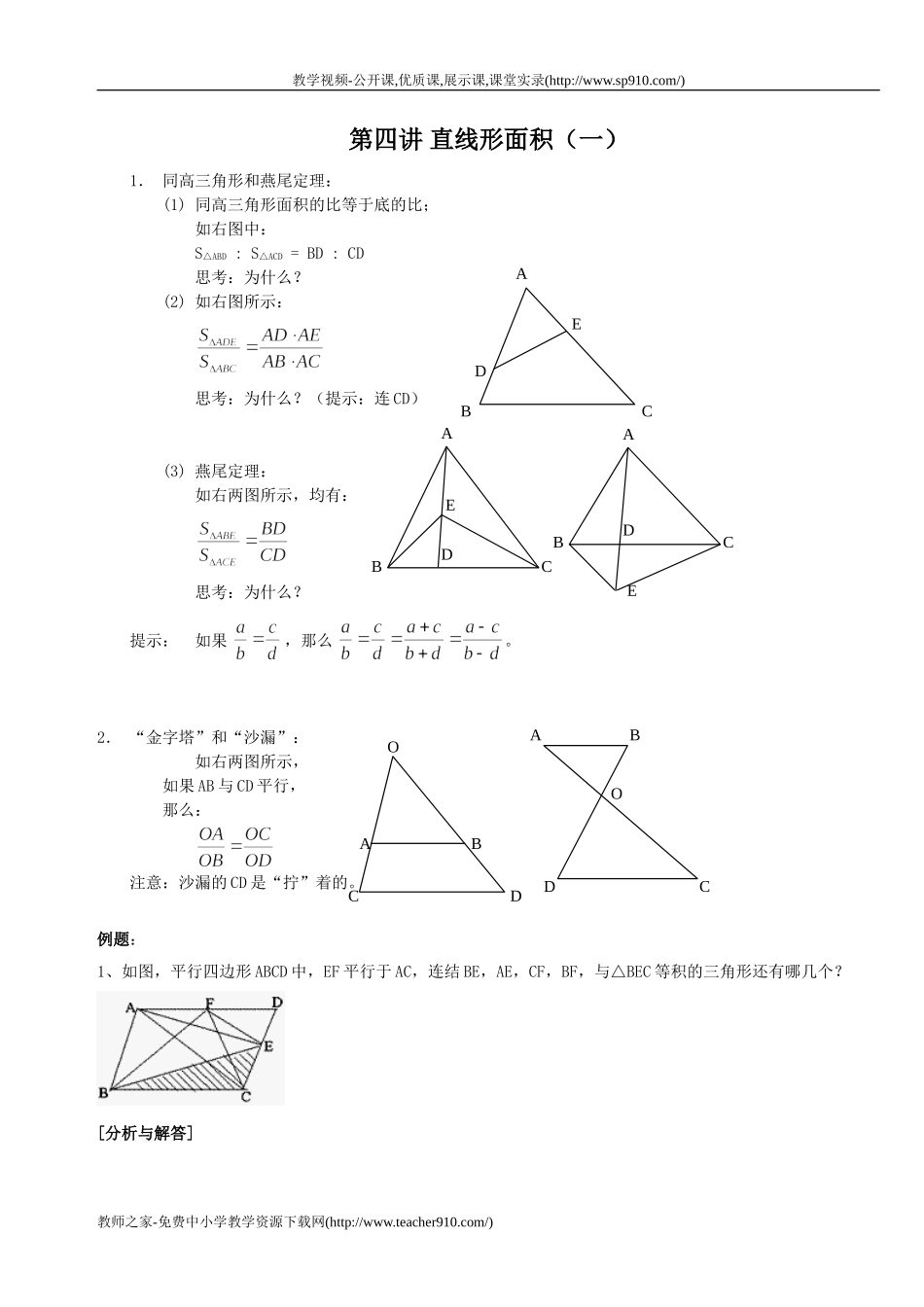
教学视频-公开课,优质课,展示课,课堂实录(http://www.sp910.com/)第四讲直线形面积(一)1.同高三角形和燕尾定理:(1)同高三角形面积的比等于底的比;如右图中:S△ABD:S△ACD=BD:CD思考:为什么?(2)如右图所示:思考:为什么?(提示:连CD)(3)燕尾定理:如右两图所示,均有:思考:为什么?提示:如果,那么。2.“金字塔”和“沙漏”:如右两图所示,如果AB与CD平行,那么:注意:沙漏的CD是“拧”着的。例题:1、如图,平行四边形ABCD中,EF平行于AC,连结BE,AE,CF,BF,与△BEC等积的三角形还有哪几个?[分析与解答]教师之家-免费中小学教学资源下载网(http://www.teacher910.com/)ABCDEABCDEABCDEOCDABODCAB教学视频-公开课,优质课,展示课,课堂实录(http://www.sp910.com/)由于图中平行线有三组:AD平行于BC,AB平行于CD,EF平行于AC,不妨依据同底等高的三角形等积来寻求等积三角形。先看与△BEC同底的三角形,若以BC边为底,这样的三角形还有△ABC,△BFC,它们两个不可能与△BEC等积,因为AE,AF都不与BC平行,也就不存在等高了,而以EC边为底的三角形还有△AEC,它的第三个顶点A与B的连线AB是与EC平行的,所以△AEC与△BEC等积。直接与△BEC等积的三角形没有了,但可以间接求,与△AEC等积的三角形必然与△BEC等积。如图中,△AEC的另一边AC与EF平行,则EF线上任意一点与A,C两点连线构成的三角形必然与△AEC等积,在EF上,只有E,F点,因此,△AFC与△AEC等积。同样的方法可找到与△AFC等积的三角形△ABF。所以与△BEC等积的三角形共有三个,它们是:△AEC,△AFC,△ABF。2、如图,在△ABC中,AD是AC的三分之一,AE是AB的四分之一,若△AED的面积是2平方厘米,那么△ABC的面积是多大?[分析与解答]连结EC,如图,因为AC=3AD,△AED与△AEC中AD,AC边上的高相同,所以△AEC的面积是△AED面积的3倍,即△AEC面积是6平方厘米,用同样方法可判断△ABC的面积且△AEC面积的四倍,所以△ABC的面积是6×4=24(平方厘米)。3、将三角形ABC的BA边延长1倍到D;CB边延长2倍到E,AC边延长3倍到F,如果三角形ABC的面积等于1,那么三角形DEF的面积是_____。[分析与解答]如图,连接CD、BF,则教师之家-免费中小学教学资源下载网(http://www.teacher910.com/)教学视频-公开课,优质课,展示课,课堂实录(http://www.sp910.com/)三角形ADC的面积=三角形ABC的面积=1;三角形BDE的面积=三角形BCD的面积×2=(1+1)×2=4;三角形CDF的面积=三角形ADC的面积×3=3;三角形BCF的面积=三角形ABC的面积×3=3;三角形BEF的面积=三角形BCF的面积×2=6;三角形DEF的面积=三角形ABC的面积+三角形ADC的面积+三角形BDE的面积+三角形CDF的面积+三角形BCF的面积+三角形BEF的面积=1+1+4+3+3+6=18。4、如图,已知AE=AC/5,CD=BC/4,BF=AB/6,那么等于多少?[分析与解答]这道题与例34很相像,但不同的是没有一个现成的单位面积。要求出这样一个比例,要求我们自己开发一个单位面积。可不可以就用大三角形的面积做单位面积呢?[解答]如图,连接AD,那么S△CDE=S△ACD×4/5=S△ABC×1/4×4/5=S△ABC×1/5教师之家-免费中小学教学资源下载网(http://www.teacher910.com/)教学视频-公开课,优质课,展示课,课堂实录(http://www.sp910.com/)同理,连接BE,那么S△AEF=S△ABE×5/6=S△ABC×1/5×5/6=S△ABC×1/6连接CF,那么S△BDF=S△BCF×3/4=S△ABC×1/6×3/4=S△ABC×1/8所以=1-1/5-1/6-1/8=5、如图,已知D是BC中点,E是CD中点,F是AC中点。三角形ABC由①~⑥这6部分组成,其中②比⑤多6平方厘米。那么三角形ABC的面积是多少?[分析与解答]仔细观察图形,我们可以发现②和⑤这两个三角形形状是一样的,并且EF是△ACD的中位线,也就是EF:AD=1:2。那么②和⑤底和高的比都是2:1(形状相同,高之比和底之比是一样的),面积比自然就是4:1了。②与⑤的面积比为4:1,并且相差6平方厘米,所以⑤的面积=6÷(4-1)=2(平方厘米)②的面积=2×4=8(平方厘米)③与④的面积均为⑤的二倍,②的一半,即4平方厘米;⑥的面积为④+⑤,即4+2=6(平方厘米)①的面积为②+③+④...