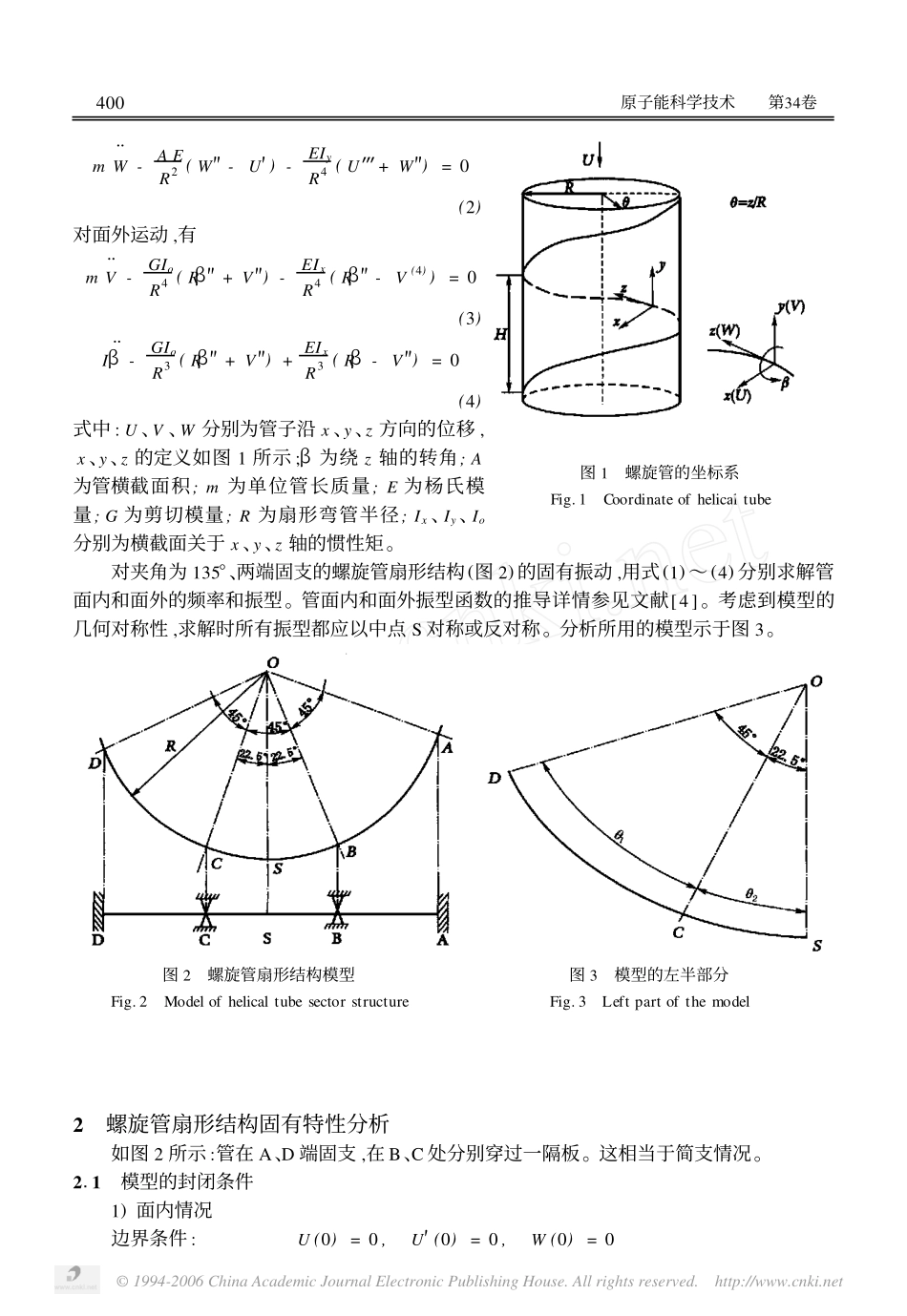
收稿日期:1999207219;修回日期:1999210220作者简介:刘瑞兰(1968—),女,河南郑州人,在读博士生,讲师,核反应堆热工专业第34卷第5期原子能科学技术Vol.34,No.52000年9月AtomicEnergyScienceandTechnologySep.2000螺旋管结构动力特性分析刘瑞兰,苏光辉,肖刚,尚智,贾斗南,沈时芳(西安交通大学能源与动力工程学院,陕西西安710049)摘要:利用弯管自由振动的解析表达式,对夹角为135°、两端固支的螺旋管扇形结构进行自由振动分析。通过给出振型函数和相应的边界条件,半解析地确定了螺旋管扇形结构的各阶频率和振型。所得结果与Chen的实验数据相一致。关键词:螺旋管扇形结构;频率;振型中图分类号:TL334文献标识码:A文章编号:100026931(2000)0520399206蒸汽发生器的设计往往重视其传热和水力特性,忽视结构动力特性。近年来,使用中出现的流弹不稳定性导致蒸汽发生器传热管大幅度振动,迫使核电站降功率运行,甚至停堆的事故屡见不鲜。因此,对蒸汽发生器动力特性进行分析研究显得十分重要。目前,国内外对直管管阵流体诱发振动研究较多,对螺旋管流弹不稳定性的研究很少。用实验的方法,Weaver[1]曾对弯管面内和面外固有频率的差异(即非对称刚度)所产生的影响进行过模拟研究。Chen[2]研究了螺旋管蒸汽发生器扇形模型在流体激励下的动态特性。作者[3]对螺旋管管阵在横向气流作用下的流弹不稳定性进行过实验研究,获得了该结构的流体力系数。本工作将对螺旋管扇形结构的动力特性进行分析研究。1螺旋管扇形结构模型的建立蒸汽发生器结构中的螺旋管缠绕较密,螺旋角为36°。用有限元动力分析方法业已证实[4]:在低频段,此螺旋管结构与平面圆环的固有振动特性十分接近。因此,可采用平面圆环近似模拟螺旋管结构的固有振动特性。L.S.S.Lee和D.J.Gorman[5~7]分别对弯管的自由振动进行过理论研究,得到了系统面内、面外振动的解析表达式。螺旋管所在的坐标系示于图1。忽略剪切变形及绕x、y轴的转动惯量,推得自由转动方程:对面内运动,有mΒ-AER2(W′-U)+EIyR4(U(4)+W�)=0(1)'1994-2006ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net图1螺旋管的坐标系Fig.1CoordinateofhelicaltubemW¨-AER2(W″-U′)-EIyR4(U�+W″)=0(2)对面外运动,有mV¨-GIoR4(Rβ″+V″)-EIxR4(Rβ″-V(4))=0(3)Iβ¨-GIoR3(Rβ″+V″)+EIxR3(Rβ-V″)=0(4)式中:U、V、W分别为管子沿x、y、z方向的位移,x、y、z的定义如图1所示;β为绕z轴的转角;A为管横截面积;m为单位管长质量;E为杨氏模量;G为剪切模量;R为扇形弯管半径;Ix、Iy、Io分别为横截面关于x、y、z轴的惯性矩。对夹角为135°、两端固支的螺旋管扇形结构(图2)的固有振动,用式(1)~(4)分别求解管面内和面外的频率和振型。管面内和面外振型函数的推导详情参见文献[4]。考虑到模型的几何对称性,求解时所有振型都应以中点S对称或反对称。分析所用的模型示于图3。图2螺旋管扇形结构模型Fig.2Modelofhelicaltubesectorstructure图3模型的左半部分Fig.3Leftpartofthemodel2螺旋管扇形结构固有特性分析如图2所示:管在A、D端固支,在B、C处分别穿过一隔板。这相当于简支情况。211模型的封闭条件1)面内情况边界条件:U(0)=0,U′(0)=0,W(0)=0004原子能科学技术第34卷©1994-2006ChinaAcademicJournalElectronicPublishingHouse.Allrightsreserved.http://www.cnki.net连续性条件:W(θ1)=0,U(θ1)=0,U′(θ1)=U′(0),U″(θ1)+W′(θ1)=U″(0)+W′(0),U(0)=0,W(0)=0振型对称时:W(θ2)=0,U′(θ2)=0,U�(θ2)=0振型反对称时:U(θ2)=0,U″(θ2)=0,Uiv(θ2)=02)面外情况边界条件:V(0)=0,V′(0)=0,B(0)=0连续性条件:V(θ1)=0,V′(θ1)=V′(0),B(θ1)-V″(θ1)=B(0)-V(0),B′(θ1)+V′(θ1)=B′(0)+V′(0),B(θ1)=B(0),V(0)=0振型对称时:V′(θ2)=0,B′(θ2)=0,V�(θ2)=0振型反对称时:V(θ2)=0,B(θ2)=0,V″(θ2)=0其中:θ1=45°×3.14159/180°=0.7854;θ2=θ1/2=0.3927。对于面外和面内振型的每种情况,均可由上述边界条件来确定振型函数的12个未知量,并用文献[4]给出的面外和面内振型解的解析表达式求解弯管的固有频率和振型。212面内振型的解对于面内振型,位移U...