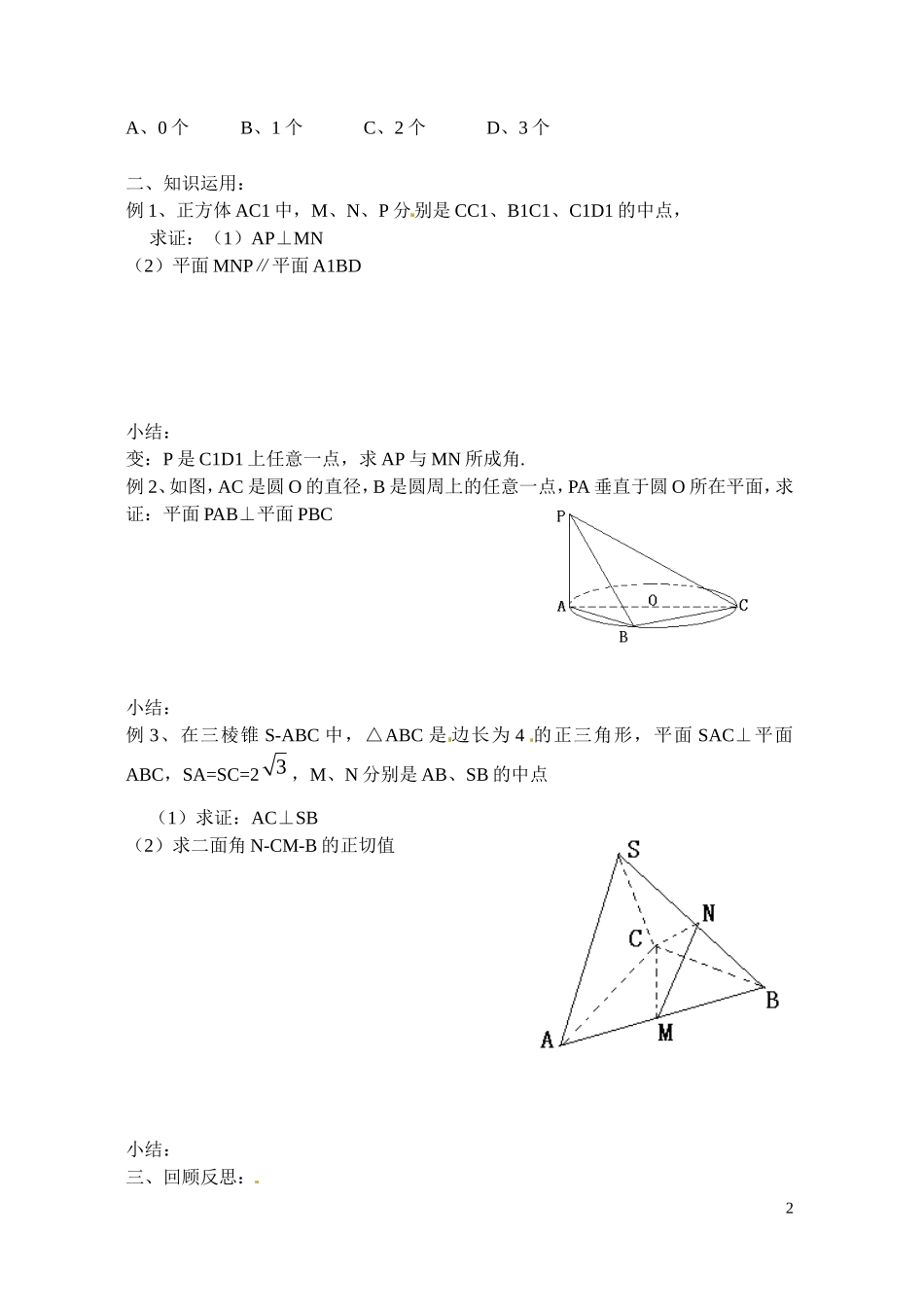
江苏省射阳县盘湾中学高中数学平面与平面的位置关系(第3课时)教案苏教版必修2教学目标:能综合运用两个平面平行的判定定理和性质定理以及两个平面垂直的判定定理和性质定理解决有关问题;注重渗透化归与转化的数学思想。教学重点:面面平行、面面垂直的判定定理、性质定理的综合运用教学难点:在具体的问题情境中探求定理成立的条件是否具备教学过程:一、学生活动:1、下列说法正确的是()A、平行于同一直线的两个平面平行B、若一个平面内两直线分别与另一个平面平行,则这两个平面平行C、若一个平面上不共线三点到另一个平面距离相等,则这两个平面平行D、若一个平面内两相交直线分别与另一个平面内两直线平行,则这两个平面平行2、若a、b表示直线,、、表示平面,则下列命题不正确的是___________(1)若a,a垂直于内任意一条直线,则(2)若=a,b,ab则(3)若,a,b,则ab(4)若,,则∥(5)若a不垂直于平面,则a不可能垂直于内无数条直线3、长方体ABCD-A1B1C1D1中,经过其对角线BD1的平面分别与棱AA1、CC1相交于两点E、F,则四边形EBFD1的形状是________________________________4、将边长为a的等边△ABC沿BC边上的高AD折成直二面角,则点A到线段BC的距离为_____________________________.5、下列命题中正确命题的个数为()(1)两个相交平面组成的图形叫做二面角(2)一个平面与二面角的棱相交,截得的图形是此二面角的平面角(3)二面角的平面角是从棱上一点出发,分别在两个平面内作射线所成角中的最小角(4)异面直线a、b分别和一个二面角的两个面垂直,则a、b所成的角与这个二面角的平面角必互补1A、0个B、1个C、2个D、3个二、知识运用:例1、正方体AC1中,M、N、P分别是CC1、B1C1、C1D1的中点,求证:(1)AP⊥MN(2)平面MNP∥平面A1BD小结:变:P是C1D1上任意一点,求AP与MN所成角.例2、如图,AC是圆O的直径,B是圆周上的任意一点,PA垂直于圆O所在平面,求证:平面PAB⊥平面PBC小结:例3、在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=23,M、N分别是AB、SB的中点(1)求证:AC⊥SB(2)求二面角N-CM-B的正切值小结:三、回顾反思:2知识:思想方法:3