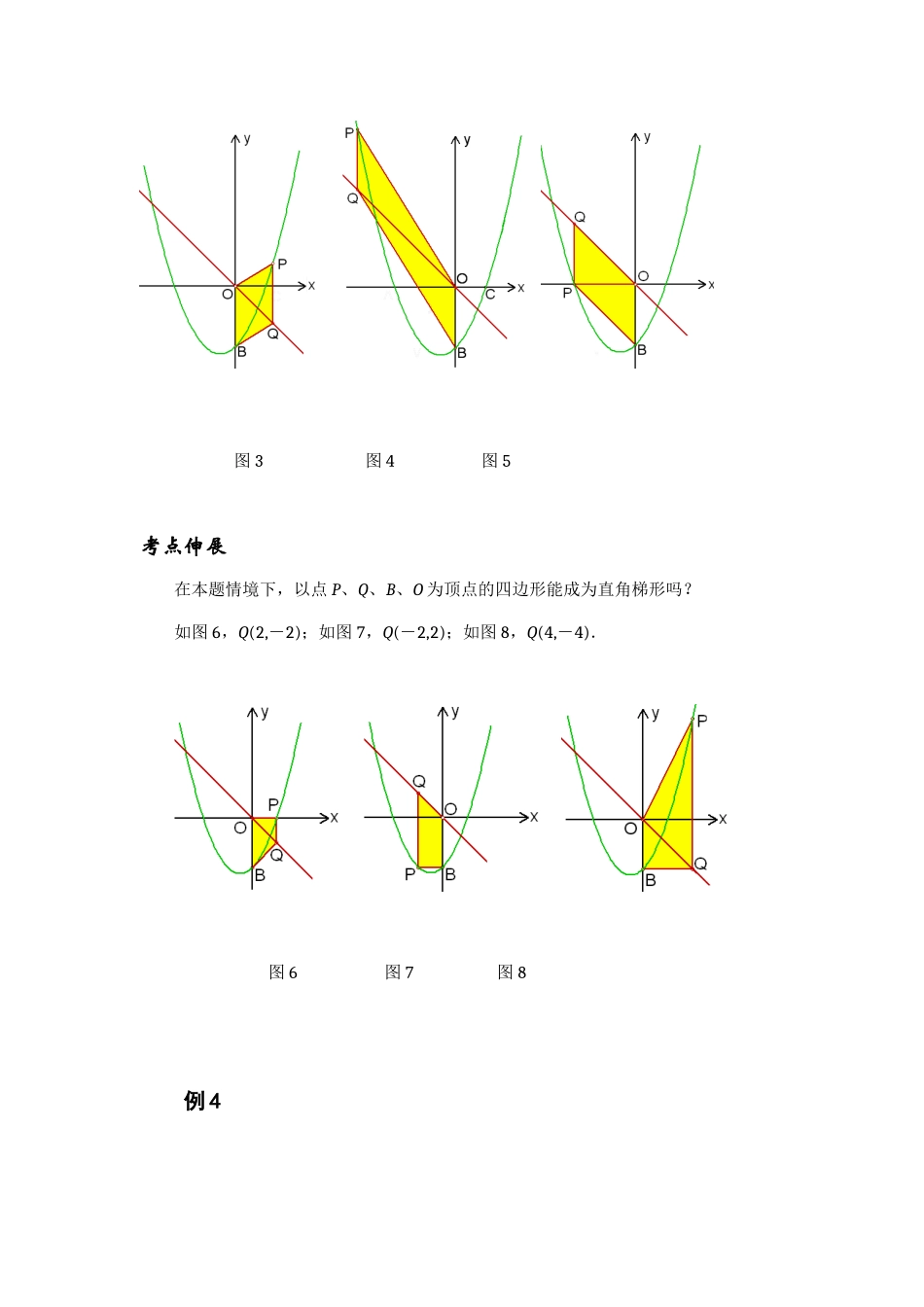
2013中考数学压轴题函数平行四边形问题(二)例3如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1图2动感体验请打开几何画板文件名“10河南23”,拖动点M在第三象限内抛物线上运动,观察S随m变化的图像,可以体验到,当D是AB的中点时,S取得最大值.拖动点Q在直线y=-x上运动,可以体验到,以点P、Q、B、O为顶点的四边形有3个时刻可以成为平行四边形,双击按钮可以准确显示.思路点拨1.求抛物线的解析式,设交点式比较简便.2.把△MAB分割为共底MD的两个三角形,高的和为定值OA.3.当PQ与OB平行且相等时,以点P、Q、B、O为顶点的四边形是平行四边形,按照P、Q的上下位置关系,分两种情况列方程.满分解答(1)因为抛物线与x轴交于A(-4,0)、C(2,0)两点,设y=a(x+4)(x-2).代入点B(0,-4),求得.所以抛物线的解析式为.(2)如图2,直线AB的解析式为y=-x-4.过点M作x轴的垂线交AB于D,那么.所以.因此当时,S取得最大值,最大值为4.(3)如果以点P、Q、B、O为顶点的四边形是平行四边形,那么PQ//OB,PQ=OB=4.设点Q的坐标为,点P的坐标为.①当点P在点Q上方时,.解得.此时点Q的坐标为(如图3),或(如图4).②当点Q在点P上方时,.解得或(与点O重合,舍去).此时点Q的坐标为(-4,4)(如图5).图3图4图5考点伸展在本题情境下,以点P、Q、B、O为顶点的四边形能成为直角梯形吗?如图6,Q(2,-2);如图7,Q(-2,2);如图8,Q(4,-4).图6图7图8例4在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1图2动感体验请打开几何画板文件名“10山西26”,拖动点M可以在直线DE上运动.分别双击按钮“DO、DM为邻边”、“DO、DN为邻边”和“DO为对角线”可以准确显示菱形.思路点拨1.第(1)题和第(2)题蕴含了OB与DF垂直的结论,为第(3)题讨论菱形提供了计算基础.2.讨论菱形要进行两次(两级)分类,先按照DO为边和对角线分类,再进行二级分类,DO与DM、DO与DN为邻边.满分解答(1)如图2,作BH⊥x轴,垂足为H,那么四边形BCOH为矩形,OH=CB=3.在Rt△ABH中,AH=3,BA=,所以BH=6.因此点B的坐标为(3,6).(2)因为OE=2EB,所以,,E(2,4).设直线DE的解析式为y=kx+b,代入D(0,5),E(2,4),得解得,.所以直线DE的解析式为.(3)由,知直线DE与x轴交于点F(10,0),OF=10,DF=.①如图3,当DO为菱形的对角线时,MN与DO互相垂直平分,点M是DF的中点.此时点M的坐标为(5,),点N的坐标为(-5,).②如图4,当DO、DN为菱形的邻边时,点N与点O关于点E对称,此时点N的坐标为(4,8).③如图5,当DO、DM为菱形的邻边时,NO=5,延长MN交x轴于P.由△NPO∽△DOF,得,即.解得,.此时点N的坐标为.图3图4考点伸展如果第(3)题没有限定点N在x轴上方的平面内,那么菱形还有如图6的情形.图5图6